编译原理——DFA的编程实现

前言：这是我学习编译原理，课程实验的内容，课程早已结束，现整理发表。

一、实验任务

编写一个C语言程序，模拟实现DFA识别字符串的过程。

---

二、实验内容

1. DFA的输入；
2. DFA的存储与读写；
3. DFA的正确性检查；
4. DFA的语言集列表显示；
5. DFA的规则字符串判定；

---

三、内容说明

1. DFA的输入：
   分别输入DFA的“字符集”、“状态集”、“开始状态”、“接受状态集”、“状态转换表”等内容，并保存在设定的变量中。

2. DFA的存储与读写：
   将上述DFA的五元组保存在一个文本文件中，扩展名指定为.dfa。请自行设计DFA文件的存储格式，并说明其含义。能将保存在内存变量中的DFA写入DFA文件，也能将DFA文件读入内存中。（思考：对稀疏DFA（转换表中为空的地方较多）或用“或”表达转换的DFA（如下的测试用例三），如何改进DFA转换表的表达。）

3. DFA的正确性检查：

• 检查所有集合的元素的唯一性。
• 检查“开始状态”是否唯一，并是否包含在“状态集”中。
• 检查“接受状态集”是否为空，并是否包含在“状态集”中。
• 检查“状态转换表”是否满足DFA的要求。
• 检查“状态转换表”并非填满时的处理是否得当。

3. DFA的语言集列表显示：
   输入待显示的字符串的最大长度N，输出以上定义的DFA的语言集中长度≤N的所有规则字符串。（提示：注意算法中while循环的次数）

4. DFA的规则字符串判定：
   输入（或用字符集随机生成）一个字符串，模拟DFA识别字符串的过程判定该字符串是否是规则字符串（属于DFA的语言集）。

---

四、测试用例

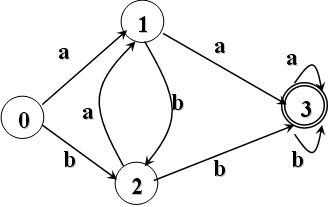
• DFA(1)

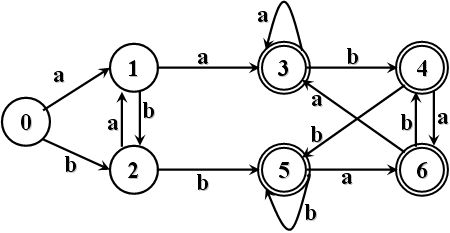
• DFA(2)

• DFA(3)

五、DFA存储格式建议

3 // 字符集中的字符个数 (以下两行也可合并成一行)
/ * o // 以空格分隔的字符集。O代表任意非/和*的字符
5 // 状态个数 (以下两行也可合并成一行)
1 2 3 4 5 // 状态编号。若约定总是用从1开始的连续数字表示，则此行可省略
1 // 开始状态的编号。若约定为1，则此行可省
1 // 结束状态个数。若约定为1，则此行可省略
5 // 结束状态的编号
2  -1  -1 // 状态1的所有出去的转换。按字符集中的字符顺序给出。-1表示出错状态
-1  3  -1
-1  4   3
5   4   3
-1  -1  -1

---

六、程序设计

• 要定义的字符、状态等。

string inputChar;           //要匹配的字符串
string charracters;         //字符集
int stateNum = 0;           //状态个数，默认为0
int currState = 1;          //开始状态编号，默认为1
int endNum = 1;             //接受状态个数，默认为1
int *acceptState = NULL;    //接受状态
int **convertFrom = NULL;   //转换表

• 从.dfa文件中读入字符、状态和转换标。
  在读取这一部分我一开始并没有就直接从文件里读取，因为我还不知道该怎么从文件里读取数据，所以我写完后对数据的输入手动输入的，这在一开始有bug的程序里也能很好的知道到底哪里错了，结果也是我调了修复一些bug后才能正常运行，在手动测试完后，我才又加入从文件输入数据的read函数，然后学习该怎么从文件里读取数据。

void init();		//手动输入
void read();		//从.dfa文件中读取数据

• 要识别字符串的输入。

void input()
{
    cout << "输入要识别的字符串" << endl;
    cin >> inputChar;
}

• DFA的识别。这个dfa的匹配的思想是
  根据状态转换表，判断是否能依据输入的字符从当前状态中转换到下一个状态，如果不行，就说明匹配不成功，输入的字符串不在dfa的状态集中。
  如果匹配完整个输入的字符串，就判断当前状态是否在给出的接受状态中，在的话，说明输入字符串是个能被匹配的字符串，不在说明不是。

void DFA()
{
    int num = 0;
    while (num < (int)inputChar.length())
    { //循环匹配输入的字符
        int y = 0;
        bool isExist = false; //检测下一个字符是否在字符集中
        for (; y < (int)charracters.length(); y++)
        {
            if (inputChar[num] == charracters[y])
            {
                isExist = true;
                break;
            }
            //任意字符匹配匹配
            else if (y == charracters.length() - 1 && charracters[y] == '?')
            {
                isExist = true;
                break;
            }
        }
        if (isExist)
        { //检测输入的字符是否能在当前状态转换表中匹配
            if (convertFrom[currState - 1][y] > 0)
            {
                currState = convertFrom[currState - 1][y];
            }
            else
            {
                cout << "当前字符匹配出错 -1 :" << num + 1 << " " << inputChar[y] << endl;
                return;
            }
        }
        else
        {
            cout << "当前字符无法出错，不存在字符集中:" << num + 1 << " " << inputChar[y] << endl;
            return;
        }
        num++;
    }
    bool notAcceptState = true; //判断当前状态是否在借号状态中
    for (int i = 0; i < endNum; i++)
    {
        if (currState == acceptState[i])
        {
            cout << "匹配成功" << endl;
            notAcceptState = false;
        }
    }
    if (notAcceptState)
    {
        cout << "字符串不在接受状态中" << endl;
    }
}

• DFA的语言集列表显示。这部分我使用递归来实现输出以上定义的DFA的语言集中长度≤N的所有规则字符串。
  具体思想是通过深度优先搜索转换表中能被当前状态匹配的字符。当匹配到能转换状态的字符时，通过一个数组记录这个字符在转换表的列下表，这用于之后匹配到一个在语言集中的字符串时输出用。
  在每次递归时，会判断当前已匹配的字符长度是否已经超过了规定的长度N，然后判断当前状态是否在接受状态中，是的话，就可以输出已经匹配的字符。其中要注意的是字符长度为N时不能继续递归了。

void outChars(int n, int *arr);	//输出函数

void isAcceptState(int currstate, int n, int *arr);	//检查函数

void searchChars(int currstate, int n, int N, int *arr){
    if (n < N) { //每次匹配完一个字符，判断已经匹配的字符串是否在dfa的语言集中    
        isAcceptState(currstate, n, arr);
    }
    else{
        isAcceptState(currstate, n, arr);
        return;
    }
    for (int i = 0; i < (int)charracters.length(); i++){
       //从开始状态根据转换表依次匹配能出去的字符并转换状态通过递归遍历
        if (convertFrom[currstate - 1][i] > 0) {
            arr[n] = i;
            n++;
            searchChars(convertFrom[currstate - 1][i], n, N, arr);
            n--;
        }
    }
}

---

七、实验测试

• 输入的dfa文件中

    第一行 为字符集
    第二行 为状态个数，默认为从状态1开始，所以不用输入开始状态
    第三行 为行为接受状态个数
    第四行 为接受状态
    第五行 开始为状态转换表。列为字符集，对应为一个二维数组，在哪个状态输入哪个字符转到哪个状态，-1为错误状态。
  

• DFA(1)的DFA文件

ab
4
1
4
2 3
4 3
2 4
4 4

• 编译运行程序
  DFA(1)

手动输入：1 ，从文件读取 0
0
输入要识别的字符串
aabb
匹配成功
输入待显示的字符串的最大长度N
5
aa
aaa
aaaa
aaaaa
aaaab
aaab
aaaba
aaabb
aab
aaba
aabaa
aabab
aabb
aabba
aabbb
abaa
abaaa
abaab
ababb
abb
abba
abbaa
abbab
abbb
abbba
abbbb
baa
baaa
baaaa
baaab
baab
baaba
baabb
babaa
babb
babba
babbb
bb
bba
bbaa
bbaaa
bbaab
bbab
bbaba
bbabb
bbb
bbba
bbbaa
bbbab
bbbb
bbbba
bbbbb

其他两个DFA就不列出结果了，要测试其他两个DFA只需要修改 read() 函数的输入文件就好，代码文件后面会给出。

此外，并不能保证除此之外的DFA都能通过，因为测试文件只有这三个，案例有限。还有这个DFA并没有达到实验的所有要求，所以要参考的请注意。

---

八、实验总结

虽然这个实验挺简单的，只需要考虑周全就能完成，但还是带给我很多麻烦的，比如第一次使用从文件中读取数据（不熟悉从文件读取的请多注意如何写，以及是怎么从文件中读取数据的，我写的比较简单，所以有疑问多拜访拜访度娘。），因为不熟悉，刚开始还要测试数据是否读取成功，从我有个手动输入的函数就知道我是怎么多生疏了。虽然生疏，但用多了，测试多了就慢慢熟悉，后面还有几个实验，会更复杂，而我也写的更复杂，会用上许多我对c++比较生疏的写法，有兴趣或者遇到困难的可以看下。

---

九、资料下载

具体代码请见DFA。