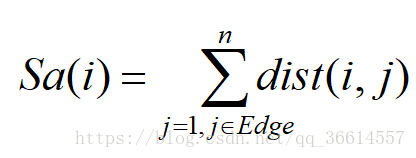基于超像素距离的图像显著性检测（Matlab2017a）

一.基本步骤

 1.导入一张图片，将图片压缩（在这里压缩成300*300）。

I=imread('timg.jpg');
I=imresize(uint8(I),[300,300]);

2.对压缩后的图片进行一次高斯平滑。

mode=fspecial('gaussian', 6, 3);
IS=imfilter(I,mode,'replicate'); 

3.对平滑后的图片进行超像素分割。

[label,num]=superpixels(IS,500);

其中，label为带有超像素的标签的与照片同大小矩阵，同一标签数字的像素属于同一超像素，num为分后的超像素个数。

4.建立一个num*5维的矩阵，用于保存超像素的信息（每行分别为每个超像素的平均横坐标，平均纵坐标，平均R，平均G，平均B）。根据原图与label的对应关系求出矩阵。

[m n]=size(label);
supmean=uint64(zeros(num,5));
labelnum=zeros(num);
%计算略

5.根据求出的超像素信息矩阵，分别求出每个超像素点的全局、边缘和局部显著性。

    1）全局

    对于超像素i，计算i到所有超像素点的距离之和，作为这个点的显著性。

为了便于显示，对其进行规范到[0,255]：

之后用Sa(i)代替超像素点的灰度值，即可得到全局显著性结果。

2)边缘

    与1)类似，唯一区别就是求距离之和时先判断j是否处于边缘（设一阈值，当某点距离边缘的距离小于阈值，则认定为边缘点）

3)与1)类似，唯一区别就是判断i与j的欧氏距离是否小于某个阈值，如果小于，则按下式计算显著性：

其中Sa(j)可为1)中j的显著性。

完整代码：

I=imread('timg.jpg');
%I=rgb2gray(I);
I=imresize(uint8(I),[300,300]);
mode=fspecial('gaussian', 6, 3);
IS=imfilter(I,mode,'replicate');  
[label,num]=superpixels(IS,500);
BW = boundarymask(label);
 %imshow(imoverlay(IS,BW,'cyan'),'InitialMagnification',100);
 %figure
[m n]=size(label);
supmean=uint64(zeros(num,5));
labelnum=zeros(num);

for i=1:m
    for j=1:n
        supmean(label(i,j),1)=supmean(label(i,j),1)+i;
        supmean(label(i,j),2)=supmean(label(i,j),2)+j;
        supmean(label(i,j),3)=(supmean(label(i,j),3)+uint64(IS(i,j,1)));
        supmean(label(i,j),4)=(supmean(label(i,j),4)+uint64(IS(i,j,2)));
        supmean(label(i,j),5)=(supmean(label(i,j),5)+uint64(IS(i,j,3)));
        labelnum(label(i,j))=labelnum(label(i,j))+1;
    end
end
for i=1:num
    supmean(i,1)=uint16(supmean(i,1)./labelnum(i));
    supmean(i,2)=uint16(supmean(i,2)./labelnum(i));
    supmean(i,3)=uint16(supmean(i,3)./labelnum(i));
    supmean(i,4)=uint16(supmean(i,4)./labelnum(i));
    supmean(i,5)=uint16(supmean(i,5)./labelnum(i));
end

IM=zeros(m,n,3);
for i=1:m
    for j=1:n
        IM(i,j,1)=uint8(supmean(label(i,j),3));
        IM(i,j,2)=uint8(supmean(label(i,j),4));
        IM(i,j,3)=uint8(supmean(label(i,j),5));
    end
end
supim=uint8(cat(3,IM(:,:,1),IM(:,:,2),IM(:,:,3)));
%imshow(supim);


%全局 
supmean=double(supmean);
dist_all=zeros(num,1);
w0=0.1;
for i=1:num
   for j=1:num
       dist_all(i)=dist_all(i)+(w0*(supmean(i,1)-supmean(j,1))^2+w0*(supmean(i,2)-supmean(j,2))^2+(supmean(i,3)-supmean(j,3))^2+(supmean(i,4)-supmean(j,4))^2+(supmean(i,5)-supmean(j,5))^2)^0.5;
   end
end
%归一化
dist_min=min(dist_all);
dist_max=max(dist_all);
for i=1:num
    dist_all(i)=(dist_all(i)-dist_min)*255/(dist_max-dist_min);
end
dist_all=uint8(dist_all);
im_all=zeros(300,300);
for i=1:m
    for j=1:n
        im_all(i,j)=dist_all(label(i,j));
    end
end
im_all=uint8(im_all);

%边缘
dist_edge=zeros(num,1);
w0=0.1;
thre=15;
for i=1:num
   for j=1:num
       if (supmean(j,1)<=thre ||supmean(j,1)>=m-thre||supmean(j,2)<=thre||supmean(j,1)>=m-thre)
         dist_edge(i)=dist_edge(i)+(w0*(supmean(i,1)-supmean(j,1))^2+w0*(supmean(i,2)-supmean(j,2))^2+(supmean(i,3)-supmean(j,3))^2+(supmean(i,4)-supmean(j,4))^2+(supmean(i,5)-supmean(j,5))^2)^0.5;
     end
   end
end
%归一化
dist_min=min(dist_edge);
dist_max=max(dist_edge);
for i=1:num
    dist_edge(i)=(dist_edge(i)-dist_min)*255/(dist_max-dist_min);
end
dist_edge=uint8(dist_edge);
im_edge=zeros(300,300);
for i=1:m
    for j=1:n
        im_edge(i,j)=dist_edge(label(i,j));
    end
end
im_edge=uint8(im_edge);

%局部

sa=ones(num,1);
w0=0.12;
w=0.18;
radius=20;
for i=1:num
    numerator=0;
    denominator=0;
    for j=1:num
       dist_ij=((supmean(i,1)-supmean(j,1))^2+(supmean(i,2)-supmean(j,2))^2);
       if i~=j
       if dist_ij<=radius^2
         dist_local=(w0*dist_ij+(supmean(i,3)-supmean(j,3))^2+(supmean(i,4)-supmean(j,4))^2+(supmean(i,5)-supmean(j,5))^2)^0.5;
         numerator=numerator+exp(-w*dist_local)*dist_all(j);
         denominator=denominator+exp(-w*dist_local);
       end
       end
    end
   sa(i)=numerator./denominator;
end
sa_max=max(sa);
sa_min=min(sa);
for i=1:num
    sa(i)=(sa(i)-sa_min)*255/(sa_max-sa_min);
end
sa=uint8(sa);
im_local=zeros(300,300);
for i=1:m
    for j=1:n
        im_local(i,j)=sa(label(i,j));
    end
end
im_local=uint8(im_local);

%显示图片 
subplot(321),imshow(I);title('Original Map');
subplot(322),imshow(imoverlay(IS,BW,'cyan'),'InitialMagnification',100);title('Superpixels Map');
supingary=rgb2gray(supim);
subplot(323),imshow(supim);title('Superixels Homogeneous Color Filling Map');
subplot(324),imshow(im_all,'Colormap',jet(255));title('In All Superpixels');
subplot(3,2,5),imshow(im_edge,'Colormap',jet(255));title('In Edge Superpixels');
subplot(3,2,6),imshow(im_local,'Colormap',jet(255));title('In Local Superpixels');

运行结果：

（显著性采用伪彩色处理）

（未采用伪彩色处理）

可见，超像素点的显著性越强，其颜色越白（橙红色），而显著性低的区域，则趋向于灰黑（蓝）色。