数据结构(12)----图(遍历、最小生成树、easyX可视化)
从图的某一顶点出发访问遍图中其余顶点,且使每一个顶点仅被访问一次,这一过程就叫做图的遍历(Traversing Graph)。
深度优先遍历(Depth_Frist_Search),也有称为深度优先搜索,简称为DFS。
DFS:它从图中某个顶点V出发,访问此顶点,然后从V的未被访问的邻接点出发深度优先遍历图,直至图中所有和V有路径相通的顶点都被访问到。若图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作为起始点,重复上述过程,直至图中所有顶点都被访问到为止。
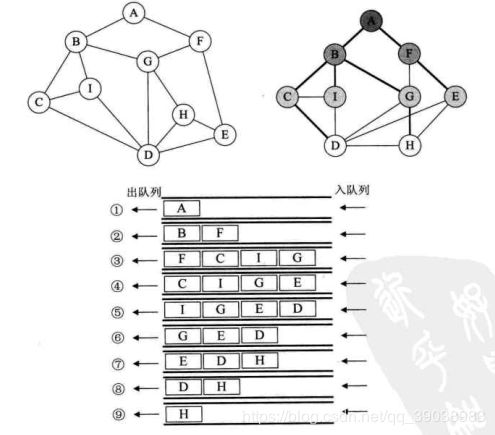
广度优先遍历(Breadth_First_Search),又称为广度优先搜索,简称BFS。
BFS:类似于树的层次遍历。
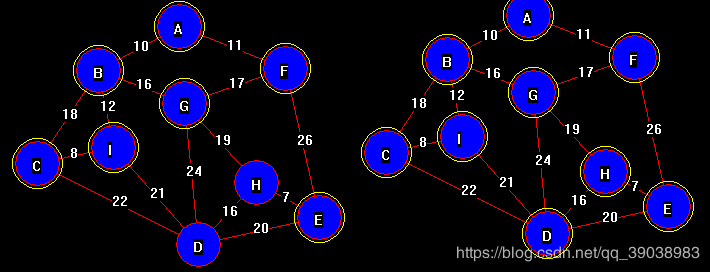
访问的次序为:A、B、F、C、G、I、E、D、H。(同一层的顺序可以不同,主要和图存储的邻接矩阵有关系)。
最小生成树
一个有 n 个结点连通图的生原图成树是的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。即生成树的权值最小。计算的方法主要有:普里姆(Prim)算法和克鲁斯卡尔(Krzuskal)算法。
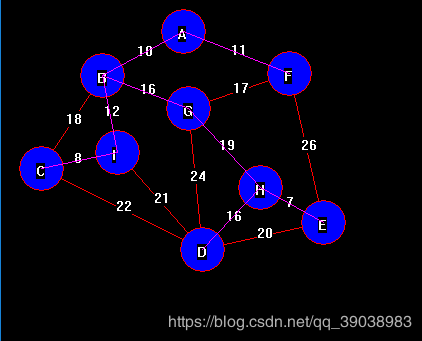
普里姆算法
顶点集合为:V,边集合为E。
1、初始化:virtexSet={X},X为集合中任意一个顶点,多选择起始点。edgeSet={}。
2、重复下列步骤直到,virtexSet中包含V中的全部顶点。
(1)、在集合E中选择权值最小的边记为
(2)、将顶点v加入集合vertexSet中,将
代码(有详细的注释,需安装easyX图形库):
void Prim(MGraph pGraph)
{
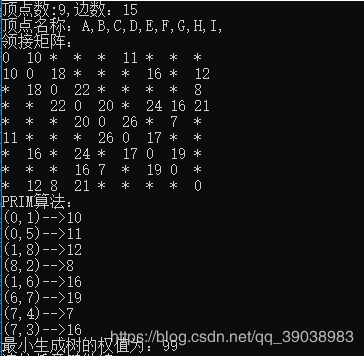
printf("PRIM算法:\n");
//要将顶点集合和取值集合结合起来,含义是:点vertexSet【j】到点j的权值大小为wightSet【j】。
int vertexSet[MAXVEX];//顶点集合
int wightSet[MAXVEX];//权值的集合
vertexSet[0] = 0;
wightSet[0] = 0;
//直到所有顶点被访问
for (int i = 0; i < pGraph.vertexNum; ++i)
{
//在开始时,顶点集合中只有点0。
vertexSet[i] = 0;
//含义:从点0到点i的边的权值为wightSet【i】
wightSet[i] = pGraph.graphEdge[0][i];
}
int x1, x2, y1, y2;//画线
setlinecolor(RGB(255, 0, 255));
//第一个顶点已经加入
for (int i = 1; i < pGraph.vertexNum; ++i)
{
int minWight = MINFINITE;
int k = 0;
for (int j = 0; j < pGraph.vertexNum; ++j)
{
//在当前取值集合中寻找最小的权值。
if (wightSet[j] != 0 && wightSet[j] < minWight)
{
minWight = wightSet[j];
k = j;
}
}
printf("(%d,%d)-->%d\n", vertexSet[k], k, pGraph.graphEdge[vertexSet[k]][k]);
_getch();
x1 = pGraph.graphVertex[vertexSet[k]].x;
y1 = pGraph.graphVertex[vertexSet[k]].y;
x2 = pGraph.graphVertex[k].x;
y2 = pGraph.graphVertex[k].y;
line(x1, y1, x2, y2);
//将已经寻找出路径的权值标记为0。因为之后还要更新wightSet的内容权值。也可以记为其他,不过0比较好处理。
wightSet[k] = 0;
//在加入新点后,需要更新顶点集合和权值集合。
for (int j = 0; j < pGraph.vertexNum; ++j)
{
//寻找从新顶点出发到未寻找顶点中比原来顶点到未寻找顶点权值小的边。
if (k != j&&wightSet[j]>pGraph.graphEdge[k][j])
{
//新顶点k到j的权值小于从原来顶点到j的权值
wightSet[j] = pGraph.graphEdge[k][j];
vertexSet[j] = k;
}
}
}
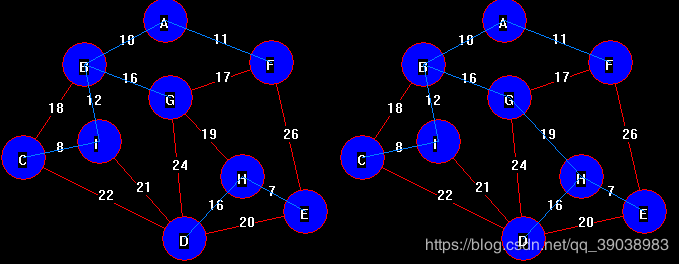
}图中紫颜色线所标记的为该图最小生成树(每按一次键画一条)。
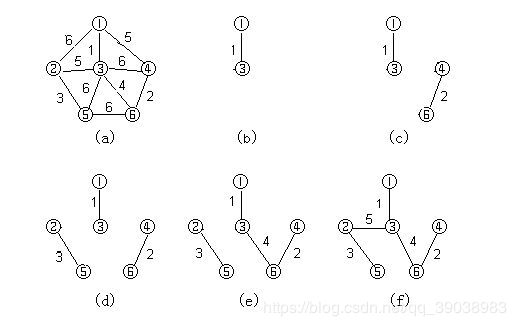
克鲁斯卡尔算法
将图中所有的点全部列出来,之后从所有的边中选择,添加的新边不能和图中的边形成回路,如果形成回路就重新选择一个小的。
代码:
bool compare(EdgeWight edgeWight1, EdgeWight edgeWight2)
{
return edgeWight1.wight < edgeWight2.wight;
}
EdgeWight* sortEdgeWight(MGraph pGraph)
{
//申请一个WightEdge类型的数组,大小为pGraph.edgeNum。
EdgeWight *wightEdge = (EdgeWight*)malloc(sizeof(EdgeWight)*(pGraph.edgeNum));
int k = 0;
for (int i = 1; i < pGraph.vertexNum; ++i)
{
for (int j = 0; j < i; ++j)
{
if (pGraph.graphEdge[i][j] != MINFINITE)
{
wightEdge[k].edgeBegin = i;
wightEdge[k].edgeEnd= j;
wightEdge[k].wight = pGraph.graphEdge[i][j];
++k;
}
}
}
//STL sort函数,在对自定义类型排序时需要告诉函数如何排序。compare为函数在239行定义。
sort(wightEdge, wightEdge + pGraph.edgeNum, compare);
return wightEdge;
}
int find(int* parent, int n)
{
//相当于将存在这点的岛走了一遍,寻找可以添加的边
while (parent[n] > -1)
{
n = parent[n];
}
return n;
}
//克鲁斯科尔的算法的难点在于:当新加一条边时,如何判断是否已经构成回路。
void Kruskal(MGraph pGraph)
{
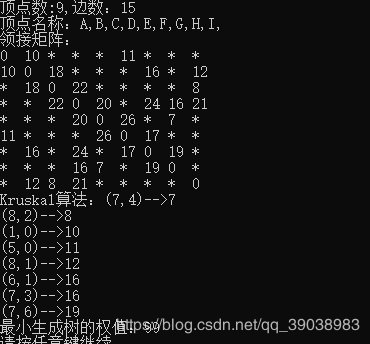
printf("Kruskal算法:");
//按照边的权值对边进行升序排序。
int wightCount = 0;
EdgeWight *wightEdge = sortEdgeWight(pGraph);
int parent[MAXVEX];//判断新添加的线是否能和原来的图构成回路
for (int i = 0; i < pGraph.vertexNum; ++i)
{
parent[i] = -1;
}
int n = -1, m = -1;
//对边按权值排序后,可以直接取出最小的边
int x1, y1, x2, y2;
setlinecolor(RGB(0, 125, 255));
for (int i = 0; i < pGraph.edgeNum; ++i)
{
n = find(parent, wightEdge[i].edgeBegin);
m = find(parent, wightEdge[i].edgeEnd);
//当n!=m时,说明新添加的点没有在图中形成回路。
if (n != m)
{
//含义:点n和点m组成的连线已经加入。
//parent实际存储的时形成的“孤岛”。
parent[n] = m;
printf("(%d,%d)-->%d\n", wightEdge[i].edgeBegin, wightEdge[i].edgeEnd, wightEdge[i].wight);
wightCount += pGraph.graphEdge[wightEdge[i].edgeBegin][wightEdge[i].edgeEnd];
_getch();
x1 = pGraph.graphVertex[wightEdge[i].edgeBegin].x;
y1 = pGraph.graphVertex[wightEdge[i].edgeBegin].y;
x2 = pGraph.graphVertex[wightEdge[i].edgeEnd].x;
y2 = pGraph.graphVertex[wightEdge[i].edgeEnd].y;
line(x1, y1, x2, y2);
}
}
printf("最小生成树的权值:%d\n",wightCount);
free(wightEdge);
}蓝线为Kruskal算法寻找的最小生成树。
普里姆算法和克鲁斯卡尔算法最终生成的最小生成树的权值相同,普里姆算法从点出发更加使用于点少边多的稠密图,而克鲁斯卡尔算法更加适用于点多边少的稀疏图。
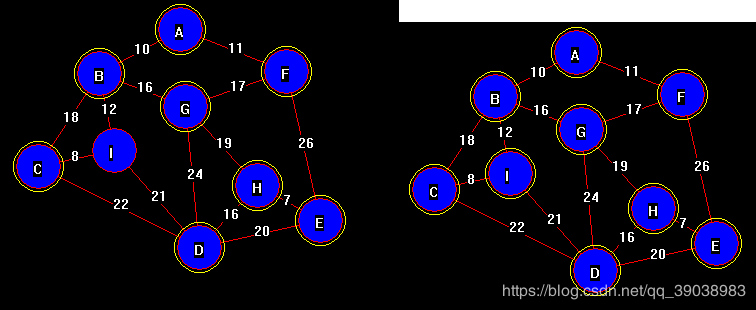
DFS图:
BFS图:
全部代码:
//.h文件
#define MAXVEX 100
#define MINFINITE 0x7FFFFFFF
typedef int EdgeType;
typedef struct
{
int edgeBegin;
int edgeEnd;
int wight;
}EdgeWight;
typedef struct
{
char data;
int x;
int y;
}Vertex;
typedef struct
{
Vertex graphVertex[MAXVEX];
EdgeType graphEdge[MAXVEX][MAXVEX];
int vertexNum;
int edgeNum;
}MGraph;
//初始化
void initGraph(MGraph* pGraph);
//生成图
void createGraph(MGraph* pGraph);
//展示图的邻接矩阵
void showGraph(MGraph pGraph);
//画图
void drawGraph(MGraph pGraph);
//DFS(深度优先搜索)
void DFSTraverse(MGraph pGraph);
//DFS
void DFS(MGraph pGraph, int* pVisited, int i);
//BFS(广度优先搜索)
void BFSTraverse(MGraph pGraph);
//最小生成树()
void MinimumSpanningTree(MGraph pGraph);
//普里姆算法
void Prim(MGraph pGraph);
EdgeWight* sortEdgeWight(MGraph pGraph);
//克鲁斯卡尔
void Kruskal(MGraph pGraph);//.cpp文件
#include "MGraph.h"
#include
#include
#include
#include
#include
#include
using namespace std;
void initGraph(MGraph* pGraph)
{
//初始化边的矩阵
for (int i = 0; i < pGraph->vertexNum; ++i)
{
for (int j = 0; j < pGraph->vertexNum; ++j)
{
if (i != j)
{
pGraph->graphEdge[i][j] = MINFINITE;
}
else
{
pGraph->graphEdge[i][j] = 0;
}
}
}
}
void createGraph(MGraph* pGraph)
{
FILE *fp(fopen("Graph.txt","r"));
fscanf(fp, "%d,%d\n", &pGraph->vertexNum, &pGraph->edgeNum);
initGraph(pGraph);
for (int i = 0; i < pGraph->vertexNum; ++i)
{
fscanf(fp, "%c,%d,%d\n", &pGraph->graphVertex[i].data, &pGraph->graphVertex[i].x, &pGraph->graphVertex[i].y);
}
int i, j, wight;
for (int k = 0; k < pGraph->edgeNum; ++k)
{
fscanf(fp, "%d,%d,%d\n", &i, &j, &wight);
pGraph->graphEdge[i][j] = wight;
pGraph->graphEdge[j][i] = wight;
//printf("%d,%d,%d\n", i, j, wight);
}
fclose(fp);
}
void showGraph(MGraph pGraph)
{
printf("顶点数:%d,边数:%d\n顶点名称:", pGraph.vertexNum, pGraph.edgeNum);
for (int i = 0; i < pGraph.vertexNum; ++i)
{
printf("%c,",pGraph.graphVertex[i]);
}
puts("\n领接矩阵:");
for (int i = 0; i < pGraph.vertexNum; ++i)
{
for (int j = 0; j < pGraph.vertexNum; ++j)
{
if (pGraph.graphEdge[i][j] == MINFINITE)
{
printf("* ");
}
else
{
printf("%-3d", pGraph.graphEdge[i][j]);
}
}
puts("");
}
}
void drawGraph(MGraph pGraph)
{
initgraph(640,480);
int x1, y1, x2, y2;
setlinecolor(RGB(255, 0, 0));
wchar_t str[100];
for (int i = 1; i < pGraph.vertexNum; ++i)
{
for (int j = 0; j < i; ++j)
{
if (pGraph.graphEdge[i][j]>0 && pGraph.graphEdge[i][j] < MINFINITE)
{
x1 = pGraph.graphVertex[i].x;
y1 = pGraph.graphVertex[i].y;
x2 = pGraph.graphVertex[j].x;
y2 = pGraph.graphVertex[j].y;
line(x1, y1, x2, y2);
swprintf(str,_T("%d"),pGraph.graphEdge[i][j]);
outtextxy((x1 + x2 - 10) / 2, (y1 + y2 - 20) / 2, (LPCTSTR)str);
}
}
}
setfillcolor(RGB(0, 0, 255));
int radio = 22;
for (int i = 0; i < pGraph.vertexNum; ++i)
{
fillcircle(pGraph.graphVertex[i].x, pGraph.graphVertex[i].y, radio);
outtextxy(pGraph.graphVertex[i].x - 5, pGraph.graphVertex[i].y - 5, pGraph.graphVertex[i].data);
}
//DFSTraverse(pGraph);
//BFSTraverse(pGraph);
MinimumSpanningTree(pGraph);
_getch();
closegraph();
}
/*
DFS:它从图中某个顶点V出发,访问此顶点,然后从V的未被访问的邻接点出发深度优先便利图,
直至图中所有和V有路径相通的顶点都被访问到。
若图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作为起始点,
重复上述过程,直至图中所有顶点都被访问到为止。
*/
void DFS(MGraph pGraph, int* pVisited, int i)
{
pVisited[i] = 1;
_getch();
setlinecolor(RGB(255,255,0));
circle(pGraph.graphVertex[i].x, pGraph.graphVertex[i].y, 25);
printf("%c-->", pGraph.graphVertex[i]);
int wight;
for (int j = 0; j < pGraph.vertexNum; ++j)
{
//如果j没有被访问过,且i到j有通路
wight = pGraph.graphEdge[i][j];
if (pVisited[j] == 0 && (wight>0 && wight < MINFINITE))
{
DFS(pGraph, pVisited, j);
}
}
}
void DFSTraverse(MGraph pGraph)
{
puts("DFS深度优先遍历结果:");
int visited[MAXVEX] = { 0 };
for (int i = 0; i < pGraph.vertexNum; ++i)
{
if (visited[i] == 0)
{
DFS(pGraph, visited, i);
}
}
}
void BFSTraverse(MGraph pGraph)
{
queue queueTra;
int visited[MAXVEX] = { 0 };
int wight, k;
for (int i = 0; i < pGraph.vertexNum; ++i)
{
if (visited[i] == 0)
{
visited[i] = 1;
queueTra.push(i);
//如果队不为空
while (!queueTra.empty())
{
_getch();
k = queueTra.front();
queueTra.pop();
setlinecolor(RGB(255, 255, 0));
circle(pGraph.graphVertex[k].x, pGraph.graphVertex[k].y, 25);
printf("%c--->", pGraph.graphVertex[k].data);
for (int j = 0; j < pGraph.vertexNum; ++j)
{
wight = pGraph.graphEdge[k][j];
if (visited[j] == 0 && (wight>0 && wight < MINFINITE))
{
queueTra.push(j);
visited[j] = 1;
}
}
}
}
}
}
void Prim(MGraph pGraph)
{
printf("PRIM算法:\n");
int minWightSum = 0;
//要将顶点集合和取值集合结合起来,含义是:点vertexSet【j】到点j的权值大小为wightSet【j】。
int vertexSet[MAXVEX];//顶点集合
int wightSet[MAXVEX];//权值的集合
vertexSet[0] = 0;
wightSet[0] = 0;
//直到所有顶点被访问
for (int i = 0; i < pGraph.vertexNum; ++i)
{
//在开始时,顶点集合中只有点0。
vertexSet[i] = 0;
//含义:从点0到点i的边的权值为wightSet【i】
wightSet[i] = pGraph.graphEdge[0][i];
}
int x1, x2, y1, y2;//画线
setlinecolor(RGB(255, 0, 255));
//第一个顶点已经加入
for (int i = 1; i < pGraph.vertexNum; ++i)
{
int minWight = MINFINITE;
int k = 0;
for (int j = 0; j < pGraph.vertexNum; ++j)
{
//在当前取值集合中寻找最小的权值。
if (wightSet[j] != 0 && wightSet[j] < minWight)
{
minWight = wightSet[j];
k = j;
}
}
printf("(%d,%d)-->%d\n", vertexSet[k], k, pGraph.graphEdge[vertexSet[k]][k]);
minWightSum += pGraph.graphEdge[vertexSet[k]][k];
_getch();
x1 = pGraph.graphVertex[vertexSet[k]].x;
y1 = pGraph.graphVertex[vertexSet[k]].y;
x2 = pGraph.graphVertex[k].x;
y2 = pGraph.graphVertex[k].y;
line(x1, y1, x2, y2);
//将已经寻找出路径的权值标记为0。因为之后还要更新wightSet的内容权值。也可以记为其他,不过0比较好处理。
wightSet[k] = 0;
//在加入新点后,需要更新顶点集合和权值集合。
for (int j = 0; j < pGraph.vertexNum; ++j)
{
//寻找从新顶点出发到未寻找顶点中比原来顶点到未寻找顶点权值小的边。
if (k != j&&wightSet[j]>pGraph.graphEdge[k][j])
{
//新顶点k到j的权值小于从原来顶点到j的权值
wightSet[j] = pGraph.graphEdge[k][j];
vertexSet[j] = k;
}
}
}
printf("最小生成树的权值为:%d\n", minWightSum);
}
bool compare(EdgeWight edgeWight1, EdgeWight edgeWight2)
{
return edgeWight1.wight < edgeWight2.wight;
}
EdgeWight* sortEdgeWight(MGraph pGraph)
{
//申请一个WightEdge类型的数组,大小为pGraph.edgeNum。
EdgeWight *wightEdge = (EdgeWight*)malloc(sizeof(EdgeWight)*(pGraph.edgeNum));
int k = 0;
for (int i = 1; i < pGraph.vertexNum; ++i)
{
for (int j = 0; j < i; ++j)
{
if (pGraph.graphEdge[i][j] != MINFINITE)
{
wightEdge[k].edgeBegin = i;
wightEdge[k].edgeEnd= j;
wightEdge[k].wight = pGraph.graphEdge[i][j];
++k;
}
}
}
//STL sort函数,在对自定义类型排序时需要告诉函数如何排序。compare为函数在239行定义。
sort(wightEdge, wightEdge + pGraph.edgeNum, compare);
return wightEdge;
}
int find(int* parent, int n)
{
//相当于将存在这点的岛走了一遍,寻找可以添加的边
while (parent[n] > -1)
{
n = parent[n];
}
return n;
}
//克鲁斯科尔的算法的难点在于:当新加一条边时,如何判断是否已经构成回路。
void Kruskal(MGraph pGraph)
{
printf("Kruskal算法:");
//按照边的权值对边进行升序排序。
int wightCount = 0;
EdgeWight *wightEdge = sortEdgeWight(pGraph);
int parent[MAXVEX];//判断新添加的线是否能和原来的图构成回路
for (int i = 0; i < pGraph.vertexNum; ++i)
{
parent[i] = -1;
}
int n = -1, m = -1;
//对边按权值排序后,可以直接取出最小的边
int x1, y1, x2, y2;
setlinecolor(RGB(0, 125, 255));
for (int i = 0; i < pGraph.edgeNum; ++i)
{
n = find(parent, wightEdge[i].edgeBegin);
m = find(parent, wightEdge[i].edgeEnd);
//当n!=m时,说明新添加的点没有在图中形成回路。
if (n != m)
{
//含义:点n和点m组成的连线已经加入。
//parent实际存储的时形成的“孤岛”。
parent[n] = m;
printf("(%d,%d)-->%d\n", wightEdge[i].edgeBegin, wightEdge[i].edgeEnd, wightEdge[i].wight);
wightCount += pGraph.graphEdge[wightEdge[i].edgeBegin][wightEdge[i].edgeEnd];
_getch();
x1 = pGraph.graphVertex[wightEdge[i].edgeBegin].x;
y1 = pGraph.graphVertex[wightEdge[i].edgeBegin].y;
x2 = pGraph.graphVertex[wightEdge[i].edgeEnd].x;
y2 = pGraph.graphVertex[wightEdge[i].edgeEnd].y;
line(x1, y1, x2, y2);
}
}
printf("最小生成树的权值:%d\n",wightCount);
free(wightEdge);
}
void MinimumSpanningTree(MGraph pGraph)
{
//Prim(pGraph);
Kruskal(pGraph);
}
int main()
{
MGraph graph;
createGraph(&graph);
showGraph(graph);
drawGraph(graph);
return 0;
} //Graph.txt(文件中只放数字,注释不能放。)
9,15 //定点数
A,183,34 //顶点名和顶点坐标
B,95,82
C,37,164
D,195,238
E,304,219
F,298,86
G,193,116
H,244,183
I,110,162
0,1,10 //边和权值
0,5,11
1,2,18
1,6,16
1,8,12
2,3,22
2,8,8
3,4,20
3,6,24
3,7,16
3,8,21
4,7,7
4,5,26
5,6,17
6,7,19