- 基于均值偏移算法的动态目标跟踪研究
Zoiny_楠
算法均值算法目标跟踪
摘要:目标跟踪技术是计算机视觉领域中重要研究课题之一,在人类生活、军事侦察、工业生产、医疗诊断、交通管理等多方面,都有广泛的应用,研究目标跟踪对人类生活、工程应用等具有现实的指导意义。在基于视觉的目标跟踪算法中,经典的Mean-Shift算法以其理论科学有效、操作简单易实现,跟踪性能较好等优势,一直是众多学者研究的热点。可算法也存在着许多缺陷。例如目标模型中混有背景信息的干扰,给目标定位带来了偏差
- UC3842控制器在flyback反激电源设计与仿真中的应用
Jacob Piao
本文还有配套的精品资源,点击获取简介:UC3842作为电流模式控制的集成控制器,在设计反激式转换器中有着广泛应用。本文档提供了使用UC3842进行flyback反激电源电路设计的详细案例,并通过Multisim14进行仿真。包含了电路设计的源文件、仿真参数设置及UC3842芯片的详细资料,旨在为工程师提供从理论到实践的完整学习平台。1.UC3842控制器特点与应用1.1UC3842控制器简介UC3
- 基于MATLAB的资源优化与工期固定-资源均衡分析方法研究【附代码】
拉勾科研工作室
matlab开发语言
算法与建模领域的探索者|专注数据分析与智能模型设计✨擅长算法、建模、数据分析matlab、python、仿真✅具体问题可以私信或查看文章底部二维码✅感恩科研路上每一位志同道合的伙伴!(1)资源均衡优化相关理论与问题分类在现代工程项目中,资源的合理分配和使用是确保项目按时完成、成本可控的关键因素。资源均衡优化作为项目管理中的核心环节,旨在通过调整资源的使用方案,使资源消耗在整个工期内尽可能平稳,避免
- 手机屏像素缺陷修复及相关液晶线路激光修复原理
syncon12
科技制造3d
摘要手机屏像素缺陷严重影响显示效果,而液晶线路异常是导致像素缺陷的关键因素之一。激光修复技术凭借高精度与非接触特性,能够有效修复液晶线路,进而改善像素显示。本文分析手机屏像素缺陷类型,探究液晶线路激光修复原理、工艺及参数优化,为提升手机屏显示质量提供理论支撑。引言随着手机屏向高分辨率、高刷新率方向发展,像素密度不断提升,像素缺陷问题愈发凸显。液晶线路作为控制像素显示的核心结构,其断路、短路、信号传
- ZYNQ无DMA的四路HP总线极限性能探索
芯作者
D1:ZYNQ设计fpga开发硬件工程智能硬件
深入挖掘AXIHP总线的直接传输潜力,突破传统DMA的性能瓶颈一、HP总线:ZYNQ系统的"高速公路"在XilinxZYNQ架构中,HP(HighPerformance)总线是连接PS(处理器系统)和PL(可编程逻辑)的关键通道。传统方案依赖DMA控制器进行数据传输,但当我们需要超低延迟或确定性响应时,无DMA的直接CPU控制成为更优选择。本文将揭示如何通过四路HP总线实现惊人的24GB/s理论带
- 基于灰色马尔科夫模型预测人口数量,是一种结合灰色系统理论(处理少数据、不确定性)与马尔科夫链(描述随机波动)的融合预测方法
利用灰色模型捕捉人口变化的总体趋势,再通过马尔科夫链修正因随机因素导致的预测偏差,从而提高预测精度。一、模型理论基础灰色系统理论原理(核心:处理少数据、部分信息未知的系统)差异信息原理:系统内外的差异是信息源,人口数据的时间序列差异蕴含变化规律。解的非唯一性原理:信息不完全时,预测结果存在多个可能区间(与马尔科夫状态划分契合)。最小信息原理:仅需少量历史数据(通常≥4个)即可建模,适合人口统计资料
- 误差的回响:反向传播算法与神经网络的惊天逆转
田园Coder
人工智能科普人工智能科普
当专家系统在20世纪80年代初期大放异彩,成为人工智能实用化的耀眼明星时,另一股曾经被宣判“死刑”的力量——连接主义(神经网络)——正在寒冬的冻土下悄然涌动,孕育着一场惊天动地的复苏。马文·明斯基和西摩·帕尔特在1969年《感知机》专著中那精准而冷酷的理论批判,如同沉重的封印,将多层神经网络的研究禁锢了近二十年。他们指出的核心死结——缺乏有效算法来训练具有隐藏层的网络——仿佛一道无法逾越的天堑。单
- 支持java8的kafka版本
兮动人
kafka分布式支持java8的kafka版本
文章目录1.Kafka支持Java8的版本范围2.官方建议与兼容性3.版本迁移建议4.关键时间点5.注意事项6.总结1.Kafka支持Java8的版本范围Kafka2.x和3.x版本:Kafka2.x和3.x版本(如2.8.0、3.0.0等)理论上支持Java8,但官方已逐步弃用对Java8的支持。Kafka3.0:官方在3.0版本中弃用Java8(但仍允许使用),并强烈建议升级到Java11或更
- 2024年BCSP-X小高组基础知识题目(模拟题)
天秀信奥编程培训
#BCXP-X模拟题北京BCSP-X试题讲解专栏BCSP-Xc++算法数据结构
一、单项选择计算机的核心部件是什么()?A.显示器B.键盘C.中央处理器(CPU)D.鼠标将十进制小数9.375转换为二进制小数,其正确的二进制表示是()。A.1001.11B.1011.11C.1001.011D.1011.011假设有一个内存显示为96MB的文件夹,里面存储的都是分辨率为1024×2048的24位图像,请问理论上存储了()张图像?(不考虑图像技术压缩对内存的优化)A.16张B.
- Maven 多模块项目调试与问题排查总结
博主简介:CSDN博客专家,历代文学网(PC端可以访问:https://literature.sinhy.com/#/?__c=1000,移动端可微信小程序搜索“历代文学”)总架构师,15年工作经验,精通Java编程,高并发设计,Springboot和微服务,熟悉Linux,ESXI虚拟化以及云原生Docker和K8s,热衷于探索科技的边界,并将理论知识转化为实际应用。保持对新技术的好奇心,乐于分
- 21个MySQL索引优化实战技巧
MySQL索引优化是提升数据库性能的关键手段,一个合理的索引设计和使用策略,往往能将查询速度提升几十倍甚至上百倍。然而,索引优化并不简单,既需要扎实的理论基础,也需要丰富的实战经验。本文总结了21个MySQL索引优化的实战技巧,从索引选择、设计到维护、监控的全生命周期,帮助你解决日常开发中的索引性能问题。基础知识回顾在具体介绍前,让我们先简单回顾索引的基础知识:MySQL常用的索引类型包括:主键索
- 蔡高厅老师 - 高等数学-阅读笔记 - 01 - 前言、函数【视频第01、02、03、】
Franklin
数学线性代数
高等数学前言;196学时,每周6课主要内容:上册一元、多元函数数,微分学、积分学、矢量代数、空间解析几何无穷级数、微分方程,多元函数微分学和积分学目的:高等数学3基:1高等数学的基本知识2高度数学的基本理论3高等数学的基本计算方法提高数学素养培养:抽象思维、逻辑推理、辩证的思想方法、空间想象能力、分析问题、解决问题的能力为进一步学习打下必要的学习基础和初等数学不同,研究的不是常量而是变量,变量和变
- 212springboot基于javaweb的城乡居民基本医疗信息管理系统医院(源码+文档+运行视频+讲解视频)
QQ2279239102
vuejavamavenSpringboothtml
项目技术:springboot+Maven+Vue等等组成,B/S模式+Maven管理等等。环境需要1.运行环境:最好是javajdk1.8,我们在这个平台上运行的。其他版本理论上也可以。2.IDE环境:IDEA,Eclipse,Myeclipse都可以。推荐IDEA;3.tomcat环境:Tomcat7.x,8.x,9.x版本均可4.硬件环境:windows7/8/101G内存以上;或者MacO
- RNN笔记
sjtu_哈基坤
LLM随笔rnn笔记人工智能
来源见此处概述RNN(RecurrentNeuralNetwork)RNN之所以称为循环神经网络,是因为一个序列的当前的输出与前面的输出也有关.具体表现是网络会对前面的信息进行记忆并且应用于当前输出的计算中.即隐藏层之间的节点也是有连接的.并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出.理论上RNN能对任何长度的序列进行处理,但是在实践中,为了降低复杂性,往往假设当前状态只与前面几
- 如何设计和训练大模型(神经网络):从入门到精通!
“学习一门技术,先找一套工具和理论研究下去;千万不要反复横跳,什么都想学”大模型作为未来重要的发展方向,很多人想学习大模型技术,但又苦于无从下手;而本公众号前前后后也写过一些怎么学习大模型技术的方法论;但大部分都是从应用的角度作为切入点。但是,有一个问题就是,如果你是一个技术从业者,想学习和设计一款属于自己的大模型,应该怎么做?设计一个自己的大模型大模型作为一门快速发展的新型技术,其理论与实现也是
- 【人工智能】微调的秘密武器:释放大模型的无限潜能
蒙娜丽宁
Python杂谈人工智能人工智能
《PythonOpenCV从菜鸟到高手》带你进入图像处理与计算机视觉的大门!解锁Python编程的无限可能:《奇妙的Python》带你漫游代码世界在人工智能迅猛发展的今天,大规模语言模型(LLMs)以其强大的通用能力席卷各行各业。然而,如何让这些通用模型在特定领域或任务中发挥最大潜力?答案是微调(Fine-tuning)。本文深入探讨微调的理论基础、技术细节与实践方法,揭示其作为解锁大模型隐藏潜力
- Python实现图像处理的快速傅里叶变换(FFT)或离散余弦变换(DCT)
闲人编程
图像处理图像处理python计算机视觉FFTDCT傅里叶离散余弦变换
目录Python实现图像处理的快速傅里叶变换(FFT)或离散余弦变换(DCT)一、引言1.1图像处理简介1.2快速傅里叶变换与离散余弦变换简介1.3本文目标与结构二、理论背景与数学原理2.1快速傅里叶变换(FFT)介绍2.2离散余弦变换(DCT)介绍2.3两者的应用领域与区别三、算法实现3.1快速傅里叶变换(FFT)实现3.1.1使用Python实现FFT3.1.2图像的频域处理3.2离散余弦变换
- 【架构专题】架构风格(上):从理论到实践的全面解析
A.说学逗唱的Coke
架构
架构风格详解:从理论到实践的全面解析一、引言在软件系统设计中,架构风格是决定系统质量与可维护性的核心要素。根据软考高级资格考试大纲要求,系统架构设计师需掌握软件架构风格的定义、分类及选型方法。本文将结合Garlan和Shaw的经典理论,结合软考实践案例,系统阐述架构风格的理论基础与应用策略。二、架构风格的定义与核心要素2.1定义软件架构风格是描述特定应用领域中系统组织方式的惯用模式,其本质是通过构
- 高级 Python 测试工程师学习提升计划
code36
python学习开发语言测试爬虫高级测试
一、测试理论与流程夯实系统梳理:每周安排3-4小时,深入研读软件测试的艺术、Google软件测试之道,重点强化功能、性能、安全性测试流程,整理流程关键节点与执行要点笔记。实践模拟:基于线上开源项目(如GitHub找小型Web应用),每月开展2次全流程测试实践,从需求分析到测试报告输出,巩固理论应用。二、Python及测试工具深化Python进阶:利用Python高级课程资料,主攻面向对象编程、装饰
- 学习笔记丨信号处理新趋势:量子计算将如何颠覆传统DSP?
棱镜研途
量子计算信号处理学习人工智能单片机网络安全密码学
在算力需求爆炸式增长的今天,传统数字信号处理(DSP)芯片正面临物理极限的严峻挑战。当经典计算机架构在摩尔定律的黄昏中挣扎时,量子计算正以颠覆性姿态崛起,准备重新定义信号处理的未来图景。目录传统DSP的瓶颈:经典架构的物理极限量子新突破:从理论优越到实用跨越量子DSP的颠覆性优势:算法与架构的双重变革应用场景:从芯片校准到生命科学技术挑战与产业化路径未来已来:量子重塑信号处理传统DSP的瓶颈:经典
- 4、理解线性代数的核心概念与应用
rice5
线性代数第五版深度解析线性代数向量空间子空间
理解线性代数的核心概念与应用1引言线性代数是现代数学的重要分支之一,广泛应用于科学、工程、计算机科学等领域。理解线性代数的基本概念和原理不仅有助于学术研究,还能够提升解决实际问题的能力。本文将深入探讨线性代数中的核心概念,帮助读者建立坚实的理论基础,并掌握实际应用技巧。2向量空间向量空间是线性代数的基础概念之一。一个向量空间(V)是指一个集合,其元素称为向量,并且这些向量之间可以进行加法运算和标量
- Kubernetes在混合云平台中的应用:跨云容器编排实战
AI云原生与云计算技术学院
AI云原生与云计算kubernetes容器云原生ai
Kubernetes在混合云平台中的应用:跨云容器编排实战关键词:Kubernetes,混合云平台,跨云容器编排,容器化,云原生摘要:本文围绕Kubernetes在混合云平台中的应用展开,详细阐述了跨云容器编排的相关技术。首先介绍了混合云及Kubernetes的背景知识,接着深入剖析Kubernetes跨云容器编排的核心概念与架构,讲解了相关算法原理和操作步骤,并通过数学模型进行了理论分析。通过具
- 2025学年湖北省职业院校技能大赛 “信息安全管理与评估”赛项 样题卷(五)
2025学年湖北省职业院校技能大赛“信息安全管理与评估”赛项样题卷(五)第二部分:网络安全事件响应、数字取证调查、应用程序安全任务书任务1:应急响应(可以培训有答案)任务2:通信数据分析取证(40分)任务3:基于Windows计算机单机取证(120分)第三部分应用程序安全任务4:C代码审计(40分)第三部分:网络安全渗透、理论技能与职业素养任务一:门户网站(60分)可以培训任务二:办公系统(60分
- 一个LoRa网关的容量多大?
豆豆在西安
LoRa网关网络服务器运维
在LoRaWAN网络部署过程中,客户最常问的问题之一就是:“一个LoRa网关能接入多少设备?”这个问题看似简单,实则涉及多个技术参数和业务场景。LoRa网关的容量并不是一个固定的数字,而是受到多种因素的影响。本文将带你深入了解LoRa网关的系统容量是如何计算的,以及影响容量的关键因素。一、LoRa网关的理论最大容量LoRa网关的容量与其使用的信道数量和扩频因子(SF)密切相关。以常见的8信道LoR
- 代码随想录|图论理论基础
1.图的种类(有向图和无向图)有向图:图中边有方向无向图:图中边无方向加权有向图:图中边是有权值和方向的,无向图也是如此2.度(无向图中有几条边连接该节点,该节点就有几度)出度:从该节点出发的边的个数入度:指向该节点边的个数3.连通性(在图中表示节点的联通情况,我们称之为连通性)连通图:在无向图中,任何两个节点都是可以到达的(可以借助其他节点)非连通图:有节点不能到达其他节点强连通图:在有向图中,
- 三生原理形式化证明:如何解决Coq工具仅覆盖部分逻辑链问题?
葫三生
三生学派算法数学建模人工智能机器学习量子计算
AI辅助创作:解决Coq工具仅覆盖部分逻辑链的问题,需结合理论扩展、工程优化与协作机制进行系统性改进,具体方案如下:一、理论层面:扩展等价判定能力补充外延式等价关系通过扩展归纳构造演算(CIC)理论,在内涵等价判定基础上增加外延式理论(如Presburger代数),增强对自然数类型等复杂结构的等价验证能力,覆盖原有工具无法判定的逻辑分支。构建抽象约束框架设计通用约束规则,使满足条件的任
- 代码随想录|图论|04广度优先搜索理论基础
Paper Clouds
图论宽度优先算法数据结构leetcodec++
广搜的使用场景广搜的搜索方式就适合于解决两个点之间的最短路径问题。因为广搜是从起点出发,以起始点为中心一圈一圈进行搜索,一旦遇到终点,记录之前走过的节点就是一条最短路。当然,也有一些问题是广搜和深搜都可以解决的,例如岛屿问题,这类问题的特征就是不涉及具体的遍历方式,只要能把相邻且相同属性的节点标记上就行。(我们会在具体题目讲解中详细来说)比如下面这个图,从start开始慢慢向外扩展,第4次扩展才到
- 51单片机基础与应用实例解析
大数据无毛兽
本文还有配套的精品资源,点击获取简介:本课程设计项目专注于51单片机的基础知识和应用实践,适合初学者。51单片机是微控制器的经典代表,广泛应用于教育和工业等领域。项目通过20个实例,涵盖C语言编程、单片机内部结构、I/O操作、定时器和计数器、中断系统、串行通信、晶振和复位电路、编程和调试、实验板使用以及项目实现等多个关键知识点,帮助学生掌握单片机的编程和应用技能,并将理论知识转化为实际操作能力。1
- 多通道时间间隔测量模块在时频行业的重要性
西安同步高经理
网络
时间间隔测量在科学研究、工程技术、日常生活等多个领域都具有重要的意义和作用,具体如下:科学研究物理学研究:在粒子物理实验中,精确测量粒子的寿命、衰变时间间隔等,有助于了解粒子的性质和相互作用规律。例如,通过测量μ子的衰变时间间隔,验证了相对论的时间膨胀效应。在原子物理中,对原子跃迁过程中时间间隔的测量,可用于研究原子的能级结构和光谱特性,为量子力学理论的发展和验证提供重要依据。天文学观测:测量天体
- 特斯拉及新能源车企笔试面试题型解析上-21期
启芯硬件笔记
经验分享PCBEMI硬件工程面试职场和发展
本专栏预计更新90期左右。当前第21期-特斯拉硬件.特斯拉作为全球领先的电动汽车、能源存储和人工智能公司,其硬件工程师岗位的招聘通常包括笔试和多轮技术面试,考察领域涵盖数字电路设计、模拟电路、嵌入式系统、电动车技术和自动驾驶等。由于特斯拉的创新性和技术领先地位,其面试问题可能更加注重实际应用和问题解决能力。笔试通常旨在考察候选人的基础理论知识、问题分析能力、电路设计与调试经验、以及对相关工具和方法
- 深入浅出Java Annotation(元注解和自定义注解)
Josh_Persistence
Java Annotation元注解自定义注解
一、基本概述
Annontation是Java5开始引入的新特征。中文名称一般叫注解。它提供了一种安全的类似注释的机制,用来将任何的信息或元数据(metadata)与程序元素(类、方法、成员变量等)进行关联。
更通俗的意思是为程序的元素(类、方法、成员变量)加上更直观更明了的说明,这些说明信息是与程序的业务逻辑无关,并且是供指定的工具或
- mysql优化特定类型的查询
annan211
java工作mysql
本节所介绍的查询优化的技巧都是和特定版本相关的,所以对于未来mysql的版本未必适用。
1 优化count查询
对于count这个函数的网上的大部分资料都是错误的或者是理解的都是一知半解的。在做优化之前我们先来看看
真正的count()函数的作用到底是什么。
count()是一个特殊的函数,有两种非常不同的作用,他可以统计某个列值的数量,也可以统计行数。
在统
- MAC下安装多版本JDK和切换几种方式
棋子chessman
jdk
环境:
MAC AIR,OS X 10.10,64位
历史:
过去 Mac 上的 Java 都是由 Apple 自己提供,只支持到 Java 6,并且OS X 10.7 开始系统并不自带(而是可选安装)(原自带的是1.6)。
后来 Apple 加入 OpenJDK 继续支持 Java 6,而 Java 7 将由 Oracle 负责提供。
在终端中输入jav
- javaScript (1)
Array_06
JavaScriptjava浏览器
JavaScript
1、运算符
运算符就是完成操作的一系列符号,它有七类: 赋值运算符(=,+=,-=,*=,/=,%=,<<=,>>=,|=,&=)、算术运算符(+,-,*,/,++,--,%)、比较运算符(>,<,<=,>=,==,===,!=,!==)、逻辑运算符(||,&&,!)、条件运算(?:)、位
- 国内顶级代码分享网站
袁潇含
javajdkoracle.netPHP
现在国内很多开源网站感觉都是为了利益而做的
当然利益是肯定的,否则谁也不会免费的去做网站
&
- Elasticsearch、MongoDB和Hadoop比较
随意而生
mongodbhadoop搜索引擎
IT界在过去几年中出现了一个有趣的现象。很多新的技术出现并立即拥抱了“大数据”。稍微老一点的技术也会将大数据添进自己的特性,避免落大部队太远,我们看到了不同技术之间的边际的模糊化。假如你有诸如Elasticsearch或者Solr这样的搜索引擎,它们存储着JSON文档,MongoDB存着JSON文档,或者一堆JSON文档存放在一个Hadoop集群的HDFS中。你可以使用这三种配
- mac os 系统科研软件总结
张亚雄
mac os
1.1 Microsoft Office for Mac 2011
大客户版,自行搜索。
1.2 Latex (MacTex):
系统环境:https://tug.org/mactex/
&nb
- Maven实战(四)生命周期
AdyZhang
maven
1. 三套生命周期 Maven拥有三套相互独立的生命周期,它们分别为clean,default和site。 每个生命周期包含一些阶段,这些阶段是有顺序的,并且后面的阶段依赖于前面的阶段,用户和Maven最直接的交互方式就是调用这些生命周期阶段。 以clean生命周期为例,它包含的阶段有pre-clean, clean 和 post
- Linux下Jenkins迁移
aijuans
Jenkins
1. 将Jenkins程序目录copy过去 源程序在/export/data/tomcatRoot/ofctest-jenkins.jd.com下面 tar -cvzf jenkins.tar.gz ofctest-jenkins.jd.com &
- request.getInputStream()只能获取一次的问题
ayaoxinchao
requestInputstream
问题:在使用HTTP协议实现应用间接口通信时,服务端读取客户端请求过来的数据,会用到request.getInputStream(),第一次读取的时候可以读取到数据,但是接下来的读取操作都读取不到数据
原因: 1. 一个InputStream对象在被读取完成后,将无法被再次读取,始终返回-1; 2. InputStream并没有实现reset方法(可以重
- 数据库SQL优化大总结之 百万级数据库优化方案
BigBird2012
SQL优化
网上关于SQL优化的教程很多,但是比较杂乱。近日有空整理了一下,写出来跟大家分享一下,其中有错误和不足的地方,还请大家纠正补充。
这篇文章我花费了大量的时间查找资料、修改、排版,希望大家阅读之后,感觉好的话推荐给更多的人,让更多的人看到、纠正以及补充。
1.对查询进行优化,要尽量避免全表扫描,首先应考虑在 where 及 order by 涉及的列上建立索引。
2.应尽量避免在 where
- jsonObject的使用
bijian1013
javajson
在项目中难免会用java处理json格式的数据,因此封装了一个JSONUtil工具类。
JSONUtil.java
package com.bijian.json.study;
import java.util.ArrayList;
import java.util.Date;
import java.util.HashMap;
- [Zookeeper学习笔记之六]Zookeeper源代码分析之Zookeeper.WatchRegistration
bit1129
zookeeper
Zookeeper类是Zookeeper提供给用户访问Zookeeper service的主要API,它包含了如下几个内部类
首先分析它的内部类,从WatchRegistration开始,为指定的znode path注册一个Watcher,
/**
* Register a watcher for a particular p
- 【Scala十三】Scala核心七:部分应用函数
bit1129
scala
何为部分应用函数?
Partially applied function: A function that’s used in an expression and that misses some of its arguments.For instance, if function f has type Int => Int => Int, then f and f(1) are p
- Tomcat Error listenerStart 终极大法
ronin47
tomcat
Tomcat报的错太含糊了,什么错都没报出来,只提示了Error listenerStart。为了调试,我们要获得更详细的日志。可以在WEB-INF/classes目录下新建一个文件叫logging.properties,内容如下
Java代码
handlers = org.apache.juli.FileHandler, java.util.logging.ConsoleHa
- 不用加减符号实现加减法
BrokenDreams
实现
今天有群友发了一个问题,要求不用加减符号(包括负号)来实现加减法。
分析一下,先看最简单的情况,假设1+1,按二进制算的话结果是10,可以看到从右往左的第一位变为0,第二位由于进位变为1。
- 读《研磨设计模式》-代码笔记-状态模式-State
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/*
当一个对象的内在状态改变时允许改变其行为,这个对象看起来像是改变了其类
状态模式主要解决的是当控制一个对象状态的条件表达式过于复杂时的情况
把状态的判断逻辑转移到表示不同状态的一系列类中,可以把复杂的判断逻辑简化
如果在
- CUDA程序block和thread超出硬件允许值时的异常
cherishLC
CUDA
调用CUDA的核函数时指定block 和 thread大小,该大小可以是dim3类型的(三维数组),只用一维时可以是usigned int型的。
以下程序验证了当block或thread大小超出硬件允许值时会产生异常!!!GPU根本不会执行运算!!!
所以验证结果的正确性很重要!!!
在VS中创建CUDA项目会有一个模板,里面有更详细的状态验证。
以下程序在K5000GPU上跑的。
- 诡异的超长时间GC问题定位
chenchao051
jvmcmsGChbaseswap
HBase的GC策略采用PawNew+CMS, 这是大众化的配置,ParNew经常会出现停顿时间特别长的情况,有时候甚至长到令人发指的地步,例如请看如下日志:
2012-10-17T05:54:54.293+0800: 739594.224: [GC 739606.508: [ParNew: 996800K->110720K(996800K), 178.8826900 secs] 3700
- maven环境快速搭建
daizj
安装mavne环境配置
一 下载maven
安装maven之前,要先安装jdk及配置JAVA_HOME环境变量。这个安装和配置java环境不用多说。
maven下载地址:http://maven.apache.org/download.html,目前最新的是这个apache-maven-3.2.5-bin.zip,然后解压在任意位置,最好地址中不要带中文字符,这个做java 的都知道,地址中出现中文会出现很多
- PHP网站安全,避免PHP网站受到攻击的方法
dcj3sjt126com
PHP
对于PHP网站安全主要存在这样几种攻击方式:1、命令注入(Command Injection)2、eval注入(Eval Injection)3、客户端脚本攻击(Script Insertion)4、跨网站脚本攻击(Cross Site Scripting, XSS)5、SQL注入攻击(SQL injection)6、跨网站请求伪造攻击(Cross Site Request Forgerie
- yii中给CGridView设置默认的排序根据时间倒序的方法
dcj3sjt126com
GridView
public function searchWithRelated() {
$criteria = new CDbCriteria;
$criteria->together = true; //without th
- Java集合对象和数组对象的转换
dyy_gusi
java集合
在开发中,我们经常需要将集合对象(List,Set)转换为数组对象,或者将数组对象转换为集合对象。Java提供了相互转换的工具,但是我们使用的时候需要注意,不能乱用滥用。
1、数组对象转换为集合对象
最暴力的方式是new一个集合对象,然后遍历数组,依次将数组中的元素放入到新的集合中,但是这样做显然过
- nginx同一主机部署多个应用
geeksun
nginx
近日有一需求,需要在一台主机上用nginx部署2个php应用,分别是wordpress和wiki,探索了半天,终于部署好了,下面把过程记录下来。
1. 在nginx下创建vhosts目录,用以放置vhost文件。
mkdir vhosts
2. 修改nginx.conf的配置, 在http节点增加下面内容设置,用来包含vhosts里的配置文件
#
- ubuntu添加admin权限的用户账号
hongtoushizi
ubuntuuseradd
ubuntu创建账号的方式通常用到两种:useradd 和adduser . 本人尝试了useradd方法,步骤如下:
1:useradd
使用useradd时,如果后面不加任何参数的话,如:sudo useradd sysadm 创建出来的用户将是默认的三无用户:无home directory ,无密码,无系统shell。
顾应该如下操作:
- 第五章 常用Lua开发库2-JSON库、编码转换、字符串处理
jinnianshilongnian
nginxlua
JSON库
在进行数据传输时JSON格式目前应用广泛,因此从Lua对象与JSON字符串之间相互转换是一个非常常见的功能;目前Lua也有几个JSON库,本人用过cjson、dkjson。其中cjson的语法严格(比如unicode \u0020\u7eaf),要求符合规范否则会解析失败(如\u002),而dkjson相对宽松,当然也可以通过修改cjson的源码来完成
- Spring定时器配置的两种实现方式OpenSymphony Quartz和java Timer详解
yaerfeng1989
timerquartz定时器
原创整理不易,转载请注明出处:Spring定时器配置的两种实现方式OpenSymphony Quartz和java Timer详解
代码下载地址:http://www.zuidaima.com/share/1772648445103104.htm
有两种流行Spring定时器配置:Java的Timer类和OpenSymphony的Quartz。
1.Java Timer定时
首先继承jav
- Linux下df与du两个命令的差别?
pda158
linux
一、df显示文件系统的使用情况,与du比較,就是更全盘化。 最经常使用的就是 df -T,显示文件系统的使用情况并显示文件系统的类型。 举比例如以下: [root@localhost ~]# df -T Filesystem Type &n
- [转]SQLite的工具类 ---- 通过反射把Cursor封装到VO对象
ctfzh
VOandroidsqlite反射Cursor
在写DAO层时,觉得从Cursor里一个一个的取出字段值再装到VO(值对象)里太麻烦了,就写了一个工具类,用到了反射,可以把查询记录的值装到对应的VO里,也可以生成该VO的List。
使用时需要注意:
考虑到Android的性能问题,VO没有使用Setter和Getter,而是直接用public的属性。
表中的字段名需要和VO的属性名一样,要是不一样就得在查询的SQL中
- 该学习笔记用到的Employee表
vipbooks
oraclesql工作
这是我在学习Oracle是用到的Employee表,在该笔记中用到的就是这张表,大家可以用它来学习和练习。
drop table Employee;
-- 员工信息表
create table Employee(
-- 员工编号
EmpNo number(3) primary key,
-- 姓
![]() ,都存在一个确定的数
,都存在一个确定的数![]() 与之对应,那么就称
与之对应,那么就称![]() 为依赖于函数
为依赖于函数![]() 的泛函,记为
的泛函,记为![]()
![]() 称为宗量。
称为宗量。![]() 是某一特定函数的整体,而不是对应于某一自变量
是某一特定函数的整体,而不是对应于某一自变量![]() 的函数值;宗量
的函数值;宗量![]() 属于的函数类称为容许函数类或者容许函数空间。
属于的函数类称为容许函数类或者容许函数空间。![]() 具有连续的导数,则它的增量可以表示如下
具有连续的导数,则它的增量可以表示如下![]()
![]() 是
是![]() 的线性函数;
的线性函数;![]() 是
是![]() 的高阶无穷小量。
的高阶无穷小量。![]() 充分小时,
充分小时,![]() 起主要作用,
起主要作用,![]() 为函数增量的线性主部,也称为函数的微分,记为
为函数增量的线性主部,也称为函数的微分,记为![]() 。
。![]() 。
。![]() 的增量可以表示为
的增量可以表示为![]()
![]() 为
为![]() 的线性连续泛函,
的线性连续泛函,![]() 为
为![]() 的高阶无穷小。记为
的高阶无穷小。记为![]() 。
。![]() 的变分为
的变分为![]() 上达到极小(极大)值,则在
上达到极小(极大)值,则在![]() 上有
上有![]() 。
。![]() 的线性连续泛函,因此,可以通过求泛函对其所有宗量的一阶偏微分得到泛函的变分。
的线性连续泛函,因此,可以通过求泛函对其所有宗量的一阶偏微分得到泛函的变分。![]() 的变分为
的变分为![]() ,使得积分型泛函
,使得积分型泛函![]()
![]() 在区间
在区间![]() 上连续,而且对于只满足某些一般条件的任意选定函数
上连续,而且对于只满足某些一般条件的任意选定函数![]() ,有
,有![]() 。
。![]() 至少是
至少是![]() 的二次可微函数,
的二次可微函数,![]() 是变量
是变量![]() ,
,![]() 和
和![]() 的连续函数,并且有二阶连续偏导数。
的连续函数,并且有二阶连续偏导数。![]() 的端点时间
的端点时间![]() 和
和![]() 是固定的,且满足如下边界条件
是固定的,且满足如下边界条件![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() 为泛函的宗量,
为泛函的宗量,![]() 为积分变量。
为积分变量。![]() ,因此
,因此![]() 。
。![]() 称为极值曲线。
称为极值曲线。 才能达到极小(极大)值。
才能达到极小(极大)值。 和
和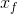 ,将积分常数
,将积分常数 和
和 固定起来。
固定起来。![]() 给定,末端
给定,末端![]() 可变,并假定沿着曲线
可变,并假定沿着曲线![]() 变化,寻找一条连续可微的极值曲线,使性能指标泛函
变化,寻找一条连续可微的极值曲线,使性能指标泛函![]() ,
,![]() ,
,![]() 和
和![]() 为泛函的宗量,
为泛函的宗量,![]() 为积分变量,为求得该泛函极值问题,引入拉格朗日乘子,并重新定义泛函为
为积分变量,为求得该泛函极值问题,引入拉格朗日乘子,并重新定义泛函为![]() 固定,所以有
固定,所以有![]() 和
和![]() ,因此
,因此![]() 和
和![]() 称为横截条件;
称为横截条件;![]() 称为边界条件。
称为边界条件。![]() 和
和![]() 。
。![]() 使得性能泛函
使得性能泛函![]() ,
,![]() 和
和![]() 为
为![]() 维宗量向量函数。
维宗量向量函数。