【hdoj3394】railway
【hdoj3394】railway
题目描述(花里胡哨)
有一个公园有n个景点,这n个景点由m条无向道路连接而成。
公园的管理员准备规划一一些形成回路的参观路线(参观路线不能经过同一个景点,是一个简单环)。如果一条道路被多条参观路线公用,那么这条路是冲突的;如果一条道路没在任何一个回路内,那么这条路是多余的道路。
问分别有多少条有冲突的路和多余的路
输入格式
包括多组数据 每组数据第一行2个整数n,m
接下来m行,每行2个整数x,y,表示从x到y有一条无向边。
输入数据以n=0,m=0结尾
输出格式
一行2个整数,表示你要求的多余的道路和冲突的道路的数量。
样例数据
input
8 10
0 1
1 2
2 3
3 0
3 4
4 5
5 6
6 7
7 4
5 7
0 0output
1 5数据规模与约定
hdoj 3394
0 < n <= 10000, 0 <= m <= 100000
时间限制:1s1s
空间限制:256MB
这题就是:给出一个无向图,求出割边的条数,并求出存在在多个环中的边的条数。
第一问求割边。
第二问求有两个简单环以上的点双的边数之和。(证明在后面)
样例解释:
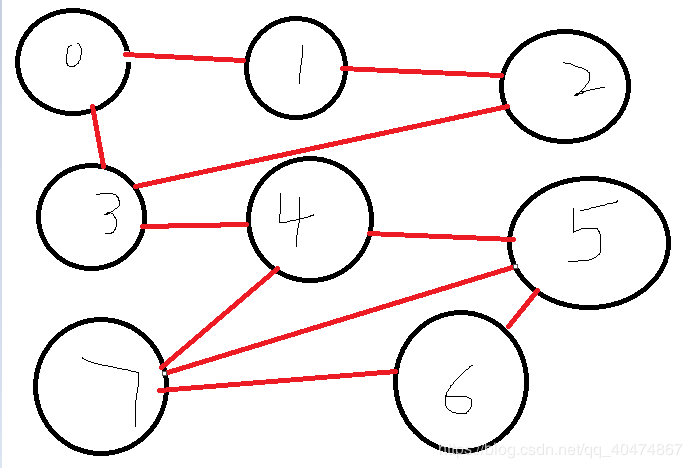
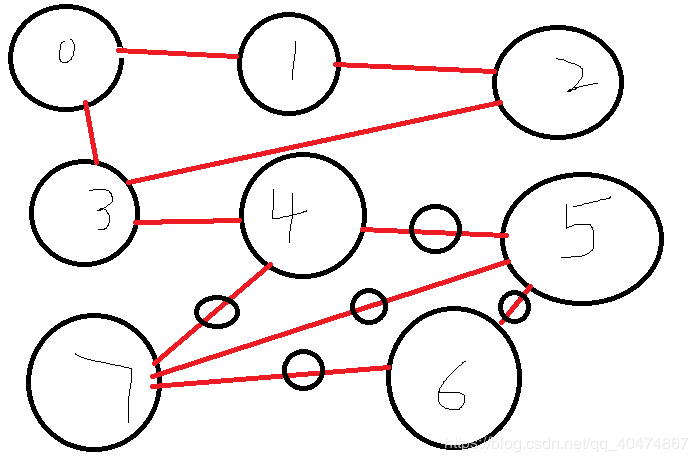
这个是图,可以知道0,1,2,3形成一个简单环,4,5,7形成简单环,5,6,7形成简单环,5,6,7,4形成简单环,那么3到4之间的路就是多余的道路,也就是割边(易证)。冲突的路就是画了圈的
5个。
其实就是有两个简单环以上的点双的边数之和。
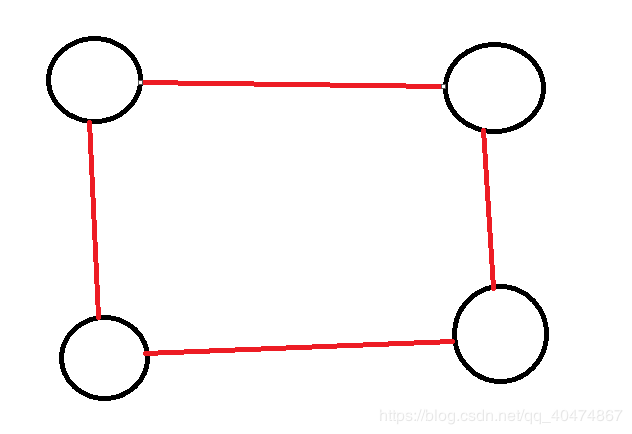
可以看一个简单的例子。
这就是一条路线,但是如果中间加一条线就不一样了。
这就是一个用两条旅游路线及以上的点双(点的数量小于边的数量)。1,4,2 1,4,3 1,2,4,3 三条路线,所以所有的路都是重复的。
所以重复的路就是有两个简单环以上的点双的边数之和了。
然后是**代码。
#include
using namespace std;
struct EE
{
int x,y;
}e[200001];
long long ans1,ans2;
int m;
int E;
int tot=1,n,x,y,num;
int u,v,w;
int top;
int dfn[100001],low[100001],d[100001],head[100001];
int color[100001],X[100001],c[100001];
int Low[100001],s[100001],a[100001];
inline void add(int a,int b)
{
e[++tot].x=head[a];
head[a]=tot;
e[tot].y=b;
}
inline void tarjan(int x,int fa)
{
dfn[x]=low[x]=Low[x]=++num;
s[++top]=x;
for(int i=head[x];i;i=e[i].x)
{
int y=e[i].y;
if(dfn[y]==0)
{
tarjan(y,i);
Low[x]=min(Low[x],Low[y]);
low[x]=min(low[x],low[y]);
if(dfn[x]v) ans2+=w/2; //判断点的数量小于边的数量,然后累加。
}
}
else
{
low[x]=min(low[x],dfn[y]);
if(i!=(fa^1))Low[x]=min(Low[x],dfn[y]);
}
}
}
inline int read()
{
int X=0,w=0; char ch=0;
while(!isdigit(ch)) {w|=ch=='-';ch=getchar();}
while(isdigit(ch)) X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
return w?-X:X;
}
int main()
{
// freopen("way.in","r",stdin);
// freopen("way.out","w",stdout);
for(;;)
{
n=read();
m=read();
if(!n&&!m) break;
memset(head,0,sizeof(head));
tot=1;
num=0;
top=0;
ans1=0;
ans2=0;
for(int i=1;i<=m;i++)
{
x=read();
y=read();
x++;
y++;
if(x!=y)
{
add(x,y);
add(y,x);
}
}
memset(dfn,0,sizeof(dfn));
for(int i=1;i<=n;i++)
{
if(!dfn[i]) tarjan(i,-1);
}
printf("%d %d\n",ans1,ans2);
}
return 0;
}