哈密顿路径
这个“哈密瓜路径”网上查了好久没搞明白,我这个的代码无奈定义了4个节点和5条边,将就混过课程设计课。
放代码和结果从我做起!欢迎大家留言!
1. 问题描述
在图G中找出一条包含所有顶点的简单路径,该路径称为哈密顿路径。
2. 基本要求
(1)图G是非完全有向图,且图G不一定存在哈密顿路径;
(2)设计算法判断图G是否存在哈密顿路径,如果存在,输出一条哈密顿路径即可;
(3)分析算法的时间复杂度。
3. 问题分析
哈密顿路径也称作哈密顿链,指在一个图中沿边访问每个顶点恰好一次的路径。寻找这样的一个路径是一个典型的NP-完全(NP-complete)问题。图中有的边可以不经过,但是不会有边被经过两次。与欧拉图的区别:欧拉图讨论的实际上是图上关于边的可行便利问题,而哈密顿图的要求与点有关。
判定:
一.Dirac定理(充分条件)
设一个无向图中有N个顶点,若所有顶点的度数大于等于N/2,则哈密顿回路一定存在(N/2指的是向上取整)。
二.基本的必要条件
设图G=
三.竞赛图(哈密顿通路)
N(N>=2)阶竞赛图一点存在哈密顿通路。
4. 概要设计
在Dirac定理的前提下构造哈密顿回路的过程:
1)任意找两个相邻的节点S和T,在其基础上扩展出一条尽量长的没有重复结点的路径。即如果S与结点v相邻,而且v不在路径S -> T上,则可以把该路径变成v -> S -> T,然后v成为新的S。从S和T分别向两头扩展,直到无法继续扩展为止,即所有与S或T相邻的节点都在路径S -> T上。
2)若S与T相邻,则路径S -> T形成了一个回路。
3) 若S与T不相邻,可以构造出来一个回路.设路径S -> T上有k+2个节点,依次为S, v1, v2, ..., vk, T.可以证明存在节点vi(i属于[1, k]),满足vi与T相邻,且vi+1与S相邻.找到这个节点vi,把原路径变成S -> vi -> T -> vi+1 ,即形成了一个回路。
4)到此为止,已经构造出来了一个没有重复节点的的回路,如果其长度为N,则哈密顿回路就找到了。如果回路的长度小于N,由于整个图是连通的,所以在该回路上,一定存在一点与回路之外的点相邻。那么从该点处把回路断开,就变回了一条路径,同时还可以将与之相邻的点加入路径。再按照步骤1的方法尽量扩展路径,则一定有新的节点被加进来。接着回到路径2。
证明:
根据鸽巢定理,既然与S和T相邻的点都在路径上,它们分布的范围只有v1,v2,---,vk这k个点,k<=N-2,跟据哈密顿回路的第一个判断条件,d(S)+d(T)>=N,那么v1,v2,---,vk这k个点中一定有至少2个点同时与S和T相连,根据鸽巢定理,肯定存在一个与S相邻的点vi和一个与T相邻的点vj,满足j=i+1。
哈密顿路径的伪代码如下:
算法:哈密顿路径
输入:哈密顿回路的起始点s,哈密顿回路中终点s之前的点t
输出:最终的哈密顿回路ans[ ]
1.初始化,令s = 1,t为s的任意一个邻接点;
2.如果ans[]中元素的个数小于n,则从t开始向外扩展,如果有可扩展点v,放入ans[]的尾部,并且t=v,并继续扩展,如无法扩展进入步骤3;
3.将当前得到的ans[]倒置,s和t互换,从t开始向外扩展,如果有可扩展点v,放入ans[]尾部,并且t=v,并继续扩展。如无法扩展进入步骤4;
3.1如果当前s和t相邻,进入步骤5。否则,遍历ans[],寻找点ans[i],使得ans[i]与t相连并且ans[i +1]与s相连,将从ans[i + 1]到t部分的ans[]倒置,t=ans[i +1],进如步骤5;
3.2如果当前ans[]中元素的个数等于n,算法结束,ans[]中保存了哈密顿回路(可看情况是否加入点s).否则,如果s与t连通,但是ans[]中的元素的个数小于n,则遍历ans[],寻找点ans[i],使得ans[i]与ans[]外的一点(j)相连,则令s=ans[i - 1],t = j,将ans[]中s到ans[i - 1]部分的ans[]倒置,将ans[]中的ans[i]到t的部分倒置,将点j加入到ans[]的尾部,转步骤2;
时间复杂度:
如果说每次到步骤5算一轮的话,那么由于每一轮当中至少有一个节点被加入到路径S -> T中,所以总的轮数肯定不超过n轮,所以时间复杂度为O(n^2).空间上由于边数非常多,所以采用邻接矩阵来存储比较适合。
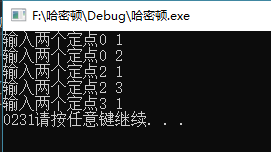
5. 编程结果
#include
#include
#define Maxsize 10
#define MAX_NO_LIMIT 10000000
typedef char Datatype;
int visited[Maxsize] = { 0 };
int s[Maxsize] = { 0 };
int count = 0;
typedef struct
{
Datatype vertex[Maxsize];
int edge[Maxsize][Maxsize];
int vertexnum, edgenum;
}graph;
void creatgraph(graph *G, Datatype a[], int n, int e)
{
int i, j, k;
G->vertexnum = n;
G->edgenum = e;
for (i = 0; ivertexnum; i++)
{
G->vertex[i] = a[i];
}
for (i = 0; ivertexnum; i++)
{
for (j = 0; jvertexnum; j++)
{
G->edge[i][j] = 0;
}
}
for (k = 0; kedgenum; k++)
{
printf("输入两个定点");
scanf_s("%d%d", &i, &j);
G->edge[i][j] = 1;
G->edge[j][i] = MAX_NO_LIMIT;
}
}
void DFS(graph *G, int v) //count是全局变量并已初始化为0
{
int j;
visited[v] = 1; //对访问点进行标记
s[count++] = v;//S表示路径,这里为开头为v
for (j = 0; j vertexnum; j++) {
if (G->edge[v][j] == 1 && visited[j] == 0)
DFS(G, j); //这里对点进行递归
}
if (j == G->vertexnum) { //取消回溯
visited[v] = 0;
count--;
}
}
int main()
{
int i;
char ch[] = { 'a','b','c','d' };
graph MG;
creatgraph(&MG, ch, 4, 5);
DFS(&MG, 0);
for (i = 0; i<4; i++)
{
printf("%d",s[i]);
}
system("pause");
return 0;
}