dfs bfs

http://www.pipioj.online/problem.php?id=1033

题目描述

PiPi喜欢把别人的名字拆开来，比如“螺”就可以拆成“虫田糸”，PiPi的语文学的不是很好，于是她决定使用编程的方式来解决这个问题。

给出一个01矩阵，1占据的部分即为需要拆的字，如果两个1分享一条边，那么它们连通。连通具有传递性，即如果a、b连通，b、c连通，则a、c连通。

连通的一系列1被看做可以拆出的一块，现在PiPi需要输出这些拆出的块（用一个01矩阵表示，并且要求矩阵的大小尽可能的小）。

为了确保输出的顺序尽可能的和书写的顺序一致，PiPi从每个块中选出最左上角的点（最左侧的点中，最靠上的）作为代表点，然后按照代表点从左到右（若相同则按从上到下）的顺序输出所有拆出的块。
输入

多组数据。

输入的第一行为两个正整数N、M，表示01矩阵的大小。

接下来N行，每行M个01字符，描述一个需要拆的字。

对于40%的数据，满足1<=N,M<=10。

对于100%的数据，满足1<=N,M<=500。

额外的样例：

11 17
00000000000000000
00001111111100000
00000000000000000
00111111111111100
00000000100000000
00000010101110000
00000110100011000
00011100100001000
00000010100000000
00000001100000000
00000000000000000

输出

按照代表点从左到右（若相同则按从上到下）的顺序输出所有拆出的块。

对于每个块，先输出其大小，然后用对应的01矩阵表示这个块。

7 13
1111111111111
0000001000000
0000001000000
0000001000000
0000001000000
0000001000000
0000011000000
3 4
0001
0011
1110
1 8
11111111
1 1
1
3 4
1110
0011
0001

样例输入

14 22
0000000000001111111100
0000000000001101101100
0000110000001111111100
0000110000001101101100
0111111110001111111100
0110110110000000000000
0110110110000011000000
0111111110001111111000
0000110000000001100000
0000110110001111111100
0111111111000111111000
0000000010001101101100
0000000000000001100000
0000000000000011100000

样例输出

10 9
000110000
000110000
111111110
110110110
110110110
111111110
000110000
000110110
111111111
000000010
5 8
11111111
11011011
11111111
11011011
11111111
8 8
00110000
11111110
00011000
11111111
01111110
11011011
00011000
00111000

提示
PIPI：大家还记得联通分量这个概念吧~

#include 
#include 
#include 
#include 
using namespace std;
int N,M;
int matrix[505][505];
int visited[505][505];
char c[505];
int dir[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
int minx,maxx,miny,maxy,n;

void dfs(int x,int y){
int i,xx,yy;
for(i=0;i<4;i++){
    xx=x+dir[i][0];
    yy=y+dir[i][1];
    if(xx>=0&&xx<N&&yy>=0&&yy<M&&!visited[xx][yy]&&matrix[xx][yy]){
minx=minx>xx?xx:minx;
maxx=maxx>xx?maxx:xx;
miny=miny>yy?yy:miny;
maxy=maxy>yy?maxy:yy;
        visited[xx][yy]=n;
        dfs(xx,yy);
    }
}
}
int main(){
int i,j,k,l;
while(scanf("%d %d",&N,&M)!=EOF){
        n=1;
    for(i=0;i<N;i++){
        scanf("%s",c);
    for(j=0;j<M;j++){
    if(c[j]=='0') matrix[i][j]=0;
    else if(c[j]=='1') matrix[i][j]=1;
    visited[i][j]=0;}
    }
    for(i=0;i<M;i++)
        for(j=0;j<N;j++)
        if(!visited[j][i]&&matrix[j][i]==1){
            visited[j][i]=n;
            minx=maxx=j;
            maxy=miny=i;
            dfs(j,i);
            printf("%d %d\n",maxx-minx+1,maxy-miny+1);
            for(k=minx;k<=maxx;k++){
                for(l=miny;l<=maxy;l++)
                if(visited[k][l]==n) printf("1");
            else printf("0");
                printf("\n");}
                n++;
        }
}//while
}

poj3894
迷宫

#include
#include 
#include 
using namespace std;
int vis[5][5];
int table[5][5];
int ans[25];
struct Point{
int x;
int y;
};
struct Point dir[4]={
{-1,0},{1,0},{0,1},{0,-1}
};

stack <struct Point> stk;
stack <struct Point>  s;
void print(stack <struct Point> stk){
stack <struct Point> s2;
if(s.empty()||s.size()>stk.size()){
    while(s.size()){s.pop();}
    while(stk.size()){
        s2.push(stk.top());
        s.push(stk.top());
        stk.pop();
    }
    while(s2.size()){
        stk.push(s2.top());
        s2.pop();
    }
}
}
void DFS(struct Point p){
    if(p.x==4&&p.y==4){
        print(stk);
        return ;
    }
    Point point;
    int i;
    for(i=0;i<4;i++){
        point.x=p.x+dir[i].x;
        point.y=p.y+dir[i].y;
    if(point.x<5&&point.x>=0&&point.y<5&&point.y>=0&&!vis[point.x][point.y]&&!table[point.x][point.y]){
        vis[point.x][point.y]=1;
        stk.push(point);
        DFS(point);
        vis[point.x][point.y]=0;
        stk.pop();
    }//if
    }

}
int main(){
    int i,j;
for(i=0;i<5;i++)
for(j=0;j<5;j++)
{
    scanf("%d",&table[i][j]);
    vis[i][j]=0;
}
struct Point p0;p0.x=0;p0.y=0;
vis[0][0]=1;
stk.push(p0);
DFS(p0);
while(s.size()){
    printf("(%d, %d)\n",s.top().x,s.top().y);
    s.pop();
}
return 0;
}

问题 D: PIPI逃亡

题目描述

PIPI被大魔王囚禁了，这一天大魔王开会去了，这正是PIPI逃亡的好机会！
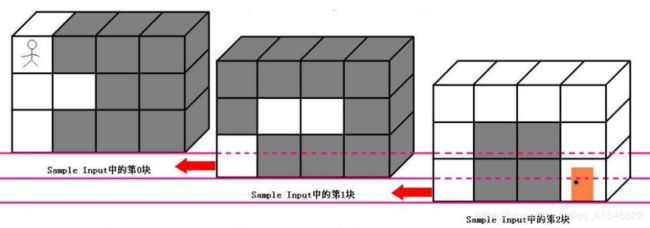
大魔王住在计算机楼,可以看成一个ABC的立方体,被表示成A个B*C的矩阵,刚开始PIPI被关在(0,0,0)的位置,离开计算机楼的门在(A-1,B-1,C-1)的位置,现在知道大魔王将在T分钟后回到计算机楼,PIPI每分钟能从一个坐标走到相邻的六个坐标中的其中一个.现在给你计算机楼的地图,请你计算出PIPI能否在大魔王回来前离开(只要走到出口就算离开,如果走到出口的时候大魔王刚好回来也算逃亡成功),如果可以请输出需要多少分钟才能离开,如果不能则输出-1.

输入

输入数据的第一行是一个正整数K,表明测试数据的数量.
每组测试数据的第一行是四个正整数A,B,C和T(1<=A,B,C<=50,1<=T<=1000),它们分别代表计算机楼的大小和大魔王回来的时间。
然后是A块输入数据(先是第0块,然后是第1块,第2块…),每块输入数据有B行,每行有C个正整数,其中0代表路,1代表墙.(如果对输入描述不清楚,可以参考Sample Input中的迷宫描述,它表示的就是上图中的迷宫)

输出

对于每组测试数据,如果PIPI能够在大魔王回来前离开,那么请输出他最少需要多少分钟,否则输出-1.

样例输入

1
3 3 4 20
0 1 1 1
0 0 1 1
0 1 1 1
1 1 1 1
1 0 0 1
0 1 1 1
0 0 0 0
0 1 1 0
0 1 1 0

样例输出

11

求最短路径用bfs适合

#include 
#include 
#include 
using namespace std;
int A,B,C,T,n;
int maze[55][55][55];
int vis[55][55][55];
int dir[6][3]={{0,0,1},{0,0,-1},{0,1,0},{0,-1,0},{1,0,0},{-1,0,0}};
struct Node {
int x;
int y;
int z;
int t;
};
queue<struct Node> Q;
int bfs(){
    int step=-1,i;
struct Node n,node;
n.x=0,n.y=0,n.z=0,n.t=0;
vis[0][0][0]=1;
Q.push(n);
while(!Q.empty()){
    n=Q.front();Q.pop();
    if(n.x==A-1&&n.y==B-1&&n.z==C-1) {step=n.t;break;}
    for(i=0;i<6;i++){
        int xx=n.x+dir[i][0];
        int yy=n.y+dir[i][1];
        int zz=n.z+dir[i][2];
        if(xx>=0&&yy>=0&&zz>=0&&xx<A&&yy<B&&zz<C&&!vis[xx][yy][zz]&&!maze[xx][yy][zz]){
           node.x=xx;node.y=yy;node.z=zz;node.t=n.t+1;
           Q.push(node);vis[xx][yy][zz]=1;
        }
    }
}
    return step;
}
int main(){
    int i,j,k;
    scanf("%d",&n);
    while(n--){
scanf("%d %d %d %d",&A,&B,&C,&T);
while(!Q.empty()) Q.pop();
for(i=0;i<A;i++)
    for(j=0;j<B;j++)
       for(k=0;k<C;k++){
    scanf("%d",&maze[i][j][k]);vis[i][j][k]=0;
}
int Move=bfs();
if(Move==-1) printf("-1\n");
else if(Move>T) printf("-1\n");
else printf("%d\n",Move);
    }
return 0;
}