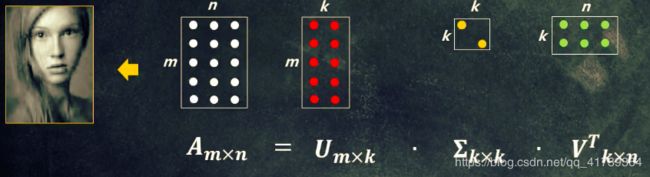奇异值分解实验:图像压缩与推荐系统
奇异值分解实验
- 奇异值分解
- 低秩近似
- 工程应用:图像压缩
- 工程应用:推荐系统
奇异值分解
只有方阵(行数等于列数)才能做特征值分解,非方阵可不可以分解为 3 3 3 个矩阵的乘积呢?
这种方式是【奇异值分解】,这种方法大学里并不学。
因为本科的线性代数主要研究方阵(除了线性系统),所以大学里并没有介绍非方阵的奇异值分解( S V D SVD SVD),奇异值分解在数据降维、语义分析、图像等领域都有十分广泛的应用,比如 P C A PCA PCA 算法里如果用数据矩阵的奇异值分解代替协方差矩阵的特征值分解,速度更快。
举个荔枝,演示一下非方阵的分解步骤。
-
A = [ 0 1 1 1 1 0 ] A=\left[ \begin{matrix} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{matrix} \right] A=⎣⎡011110⎦⎤
-
求出矩阵 A T A A^{T}A ATA 和 A A T AA^{T} AAT:
A T A = [ 0 1 1 1 1 0 ] [ 0 1 1 1 1 0 ] = [ 2 1 1 2 ] A^{T}A=\left[ \begin{matrix} 0 & 1 &1\\ 1 & 1 & 0 \end{matrix} \right]\left[ \begin{matrix} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{matrix} \right]=\left[ \begin{matrix} 2 & 1 \\ 1 & 2 \end{matrix} \right] ATA=[011110]⎣⎡011110⎦⎤=[2112]
A A T = [ 0 1 1 1 1 0 ] [ 0 1 1 1 1 0 ] = [ 1 1 0 1 2 1 0 1 1 ] AA^{T}=\left[ \begin{matrix} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{matrix} \right]\left[ \begin{matrix} 0 & 1 &1\\ 1 & 1 & 0 \end{matrix} \right]=\left[ \begin{matrix} 1 & 1 & 0\\ 1 & 2 & 1\\ 0 & 1 & 1 \end{matrix} \right] AAT=⎣⎡011110⎦⎤[011110]=⎣⎡110121011⎦⎤发现 A T A A^{T}A ATA 和 A A T AA^{T} AAT 都是实对称矩阵,必然可以做特征值分解。
-
因此,分别求出 A T A A^{T}A ATA 和 A A T AA^{T} AAT 的特征值和特征向量:
A T A A^{T}A ATA 有俩组, λ 1 = 3 v 1 = [ 1 / 2 1 / 2 ] λ 2 = 1 v 2 = [ − 1 / 2 1 / 2 ] ~~~\lambda_{1}=3~~~v_{1}=\left[ \begin{matrix} 1/\sqrt{2}\\ 1/\sqrt{2} \end{matrix} \right]~~~~~~~~~~~~~~~~\lambda_{2}=1~~~v_{2}=\left[ \begin{matrix} -1/\sqrt{2}\\ 1/\sqrt{2} \end{matrix} \right] λ1=3 v1=[1/21/2] λ2=1 v2=[−1/21/2]
A A T AA^{T} AAT 有三组, λ 1 = 3 u 1 = [ 1 / 6 2 / 6 1 / 6 ] λ 2 = 1 u 2 = [ 1 / 2 0 − 1 / 2 ] λ 3 = 1 u 3 = [ 1 / 3 − 1 / 3 1 / 3 ] ~~~\lambda_{1}=3~~~u_{1}=\left[ \begin{matrix} 1/\sqrt{6}\\ 2/\sqrt{6}\\ 1/\sqrt{6} \end{matrix} \right]~~~~~~~~~~~~~~~\lambda_{2}=1~~~u_{2}=\left[ \begin{matrix} 1/\sqrt{2}\\ 0\\ -1/\sqrt{2} \end{matrix} \right]~~~~~~~~~~~~~~~~\lambda_{3}=1~~~u_{3}=\left[ \begin{matrix} 1/\sqrt{3}\\ -1/\sqrt{3}\\ 1/\sqrt{3} \end{matrix} \right] λ1=3 u1=⎣⎡1/62/61/6⎦⎤ λ2=1 u2=⎣⎡1/20−1/2⎦⎤ λ3=1 u3=⎣⎡1/3−1/31/3⎦⎤
-
将 A A T AA^{T} AAT 的特征向量横向拼成矩阵 U U U:
U = [ 1 / 6 1 / 2 1 / 3 2 / 6 0 − 1 / 3 1 / 6 − 1 / 2 1 / 3 ] U=\left[ \begin{matrix} 1/\sqrt{6} & 1/\sqrt{2} & 1/\sqrt{3}\\ 2/\sqrt{6} & 0 & -1/\sqrt{3}\\ 1/\sqrt{6} & -1/\sqrt{2} & 1/\sqrt{3} \end{matrix} \right] U=⎣⎡1/62/61/61/20−1/21/3−1/31/3⎦⎤
U U U 是正交矩阵,因为TA的列向量俩俩正交,且都是单位向量。
-
将 A T A A^{T}A ATA 和 A A T AA^{T} AAT 的相同特征值开方,拼成矩阵 ∑ \sum ∑:

拼成矩阵 ∑ \sum ∑: l a m b d a 1 = 3 , l a m b d a 2 = 1 − > σ 1 = 3 , σ 2 = 1 − > ∑ = [ 3 0 0 1 0 0 ] lambda_{1}=3,~lambda_{2}=1~~~->~~~\sigma_{1}=\sqrt{3},~\sigma_{2}=\sqrt{1}~~~->~~~\sum=\left[ \begin{matrix} \sqrt{3} & 0 \\ 0 & \sqrt{1} \\ 0 & 0 \end{matrix} \right] lambda1=3, lambda2=1 −> σ1=3, σ2=1 −> ∑=⎣⎡300010⎦⎤
P.S. σ 1 、 σ 2 \sigma_{1}、\sigma_{2} σ1、σ2 的摆放顺序与特征向量一致。
-
将 A T A A^{T}A ATA 的特征向量横向拼成一个矩阵 V V V:
V = [ 1 / 2 − 1 / 2 1 / 2 1 / 2 ] − > V T = [ 1 / 2 1 / 2 − 1 / 2 1 / 2 ] V=\left[ \begin{matrix} 1/\sqrt{2}& -1/\sqrt{2}\\ 1/\sqrt{2}& 1/\sqrt{2} \end{matrix} \right]~~~->~~~V^{T}=\left[ \begin{matrix} 1/\sqrt{2}& 1/\sqrt{2}\\ -1/\sqrt{2}& 1/\sqrt{2} \end{matrix} \right] V=[1/21/2−1/21/2] −> VT=[1/2−1/21/21/2]
P.S. V T V_{T} VT 也是正交矩阵,因为TA的列向量俩俩正交,且是单位向量。
-
最后,将 U ⋅ ∑ ⋅ V T U·\sum·V^{T} U⋅∑⋅VT 发现结果等于原矩阵 A A A,说明 矩阵 A A A 可以分解为 U ∑ V T U \sum V^{T} U∑VT。
U ⋅ ∑ ⋅ V T = [ 1 / 6 1 / 2 1 / 3 2 / 6 0 − 1 / 3 1 / 6 − 1 / 2 1 / 3 ] [ 3 0 0 1 0 0 ] [ 1 / 2 1 / 2 − 1 / 2 1 / 2 ] = [ 0 1 1 1 1 0 ] = A U·\sum·V^{T}=\left[ \begin{matrix} 1/\sqrt{6} & 1/\sqrt{2} & 1/\sqrt{3}\\ 2/\sqrt{6} & 0 & -1/\sqrt{3}\\ 1/\sqrt{6} & -1/\sqrt{2} & 1/\sqrt{3} \end{matrix} \right]\left[ \begin{matrix} \sqrt{3} & 0 \\ 0 & \sqrt{1} \\ 0 & 0 \end{matrix} \right]\left[ \begin{matrix} 1/\sqrt{2}& 1/\sqrt{2}\\ -1/\sqrt{2}& 1/\sqrt{2} \end{matrix} \right]=\left[ \begin{matrix} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{matrix} \right]=A U⋅∑⋅VT=⎣⎡1/62/61/61/20−1/21/3−1/31/3⎦⎤⎣⎡300010⎦⎤[1/2−1/21/21/2]=⎣⎡011110⎦⎤=A
-
虽然这只是一个 3 ∗ 2 3*2 3∗2 的矩阵的分解过程,但推广到 m ∗ n m*n m∗n 的矩阵,按照这样的步骤同样可以分解为三个矩阵的乘积,这种分解方式就是【奇异值分解】。
-
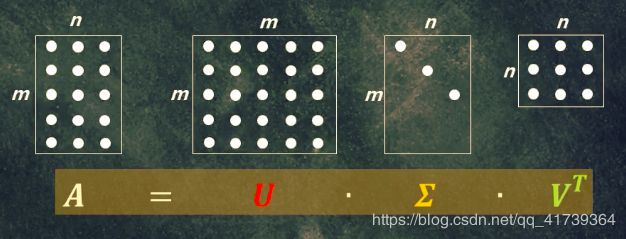
奇异值分解: A = U ∑ V T A=U \sum V^{T} A=U∑VT
A = m ∗ n A=m*n~ A=m∗n , 矩阵 A A A 的尺寸是 m ∗ n m*n m∗n
U = m ∗ m U=m*m~ U=m∗m ,矩阵 U U U 的尺寸是 m ∗ m m*m m∗m,其列向量称为 矩阵 A A A 的左奇异向量;
∑ = m ∗ n \sum=m*n~ ∑=m∗n ,矩阵 ∑ \sum ∑ 的尺寸是 m ∗ n m*n m∗n,其对角线上的值称为 矩阵 A A A 的奇异值;
V T = n ∗ n V^{T}=n*n~ VT=n∗n , 矩阵 V T V^{T} VT 的尺寸是 n ∗ n n*n n∗n,其列向量称为 矩阵 A A A 的右奇异向量。
低秩近似
我们可以把矩阵看成一种变换,把矩阵乘法当成线性变换时,找出变换矩阵的特征值和特征向量,实际上就是找出变换矩阵的主要变换方向。
也可以说是,特征值和特征向量代表了一个方阵的【固有信息】。
特征值分解是奇异值分解的特例,特征值分解只能分解方阵,奇异值分解可以分解任意形状的矩阵。
因此,奇异值及奇异向量可以说是代表了一个 m ∗ n m*n m∗n 矩阵的【固有信息】。
奇异值越大,代表的信息就越多。
另外,如果我们在奇异值矩阵 ∑ \sum ∑ 中,将奇异值从大到小排列,就会发现奇异值下降特别快。
很多情况下,前 K K K 个奇异值的和就占了全部奇异值之和的 90 90 90%。
也就是说,前 K K K 个奇异值就足以代表整个矩阵的【固有信息】!!
所以,可以用 最大的 K K K 个奇异值及对应的左右奇异向量来近似矩阵。
这种理论,就被称为【低秩近似】。
来看一个 7 ∗ 5 7*5 7∗5 的矩阵,使用【低秩近似】的实例!!
-
[ 1 1 1 0 0 3 3 3 0 0 4 4 4 0 0 5 5 5 0 0 0 2 0 4 4 0 0 0 5 5 0 1 0 2 2 ] 奇 异 值 分 解 后 − > [ 0.13 0.02 − 0.01 0.41 0.07 − 0.03 0.55 0.09 − 0.04 0.68 0.11 − 0.05 0.15 − 0.59 0.65 0.07 − 0.73 − 0.67 0.07 − 0.29 0.32 ] [ 12.4 0 0 0 9.5 0 0 0 1.3 ] [ 0.56 0.590 0.56 0.09 0.090 0.12 − 0.02 0.12 − 0.69 − 0.69 0.40 − 0.80 0.40 0.09 0.090 ] \left[ \begin{matrix} 1 & 1 & 1 & 0 & 0 \\ 3 & 3 & 3 & 0 & 0 \\ 4 & 4 & 4 & 0 & 0 \\ 5 & 5 & 5 & 0 & 0 \\ 0 & 2 & 0 & 4 & 4 \\ 0 & 0 & 0 & 5 & 5 \\ 0 & 1 & 0 & 2 & 2 \end{matrix} \right] ~~~奇异值分解后 ~~~->~~~\left[ \begin{matrix} 0.13 & 0.02 & -0.01 \\ 0.41 & 0.07 & -0.03 \\ 0.55 & 0.09 & -0.04 \\ 0.68 & 0.11 & -0.05 \\ 0.15 & -0.59 & 0.65 \\ 0.07 & -0.73 & -0.67 \\ 0.07 & -0.29 & 0.32 \end{matrix} \right]\left[ \begin{matrix} 12.4 & 0 & 0\\ 0 & 9.5 & 0 \\ 0 & 0 & 1.3 \end{matrix} \right]\left[ \begin{matrix} 0.56 & 0.590 & 0.56 & 0.09 & 0.090 \\ 0.12 & -0.02 & 0.12 & -0.69 & -0.69 \\ 0.40 & -0.80 & 0.40 & 0.09 & 0 .090 \end{matrix} \right] ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡13450001345201134500000004520000452⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤ 奇异值分解后 −> ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0.130.410.550.680.150.070.070.020.070.090.11−0.59−0.73−0.29−0.01−0.03−0.04−0.050.65−0.670.32⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎡12.40009.50001.3⎦⎤⎣⎡0.560.120.400.590−0.02−0.800.560.120.400.09−0.690.090.090−0.690.090⎦⎤
奇异值分解: A = U ∑ V T A=U \sum V^{T} A=U∑VT,看中间的 ∑ \sum ∑矩阵: [ 12.4 0 0 0 9.5 0 0 0 1.3 ] \left[ \begin{matrix} 12.4 & 0 & 0\\ 0 & 9.5 & 0 \\ 0 & 0 & 1.3 \end{matrix} \right] ⎣⎡12.40009.50001.3⎦⎤。
发现奇异值有 3 3 3 个,分别是 12.4 、 9.5 、 1.3 12.4、9.5、1.3 12.4、9.5、1.3,我们只用前面俩个奇异值来算一下,占总奇异值的比例:
- 12.4 + 9.5 12.4 + 9.5 + 1.3 ≈ 94.4 \frac{12.4+9.5}{12.4+9.5+1.3}\approx94.4 12.4+9.5+1.312.4+9.5≈94.4%
这个比例很大了,所以我们可以认为前面俩个奇异值,及其对应的左右奇异向量足以代表原来的矩阵。把这些部分截取下来:
- [ 0.13 0.02 0.41 0.07 0.55 0.09 0.68 0.11 0.15 − 0.59 0.07 − 0.73 0.07 − 0.29 ] [ 12.4 0 0 9.5 ] [ 0.56 0.590 0.56 0.09 0.090 0.12 − 0.02 0.12 − 0.69 − 0.69 ] ≈ [ 0.92 0.95 0.92 0.01 0.01 2.91 3.01 2.91 − 0.01 − 0.01 3.90 4.04 3.90 0.01 0.01 4.82 5.00 4.82 0.03 0.03 0.70 0.53 0.70 4.11 4.11 − 0.7 1.34 − 0.7 4.78 4.78 0.32 0.23 0.32 2.01 2.01 ] \left[ \begin{matrix} 0.13 & 0.02 \\ 0.41 & 0.07 \\ 0.55 & 0.09 \\ 0.68 & 0.11 \\ 0.15 & -0.59 \\ 0.07 & -0.73 \\ 0.07 & -0.29 \end{matrix} \right]\left[ \begin{matrix} 12.4 & 0 \\ 0 & 9.5 \\ \end{matrix} \right]\left[ \begin{matrix} 0.56 & 0.590 & 0.56 & 0.09 & 0.090 \\ 0.12 & -0.02 & 0.12 & -0.69 & -0.69 \end{matrix} \right]\approx\left[ \begin{matrix} 0.92 & 0.95 & 0.92 & 0.01 & 0.01 \\ 2.91 & 3.01 & 2.91 & -0.01 & -0.01 \\ 3.90 & 4.04 & 3.90 & 0.01 & 0.01 \\ 4.82 & 5.00 & 4.82 & 0.03 & 0.03 \\ 0.70 & 0.53 & 0.70 & 4.11 & 4.11 \\ -0.7 & 1.34 & -0.7 & 4.78 & 4.78 \\ 0.32 & 0.23 & 0.32 & 2.01 & 2.01 \end{matrix} \right] ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0.130.410.550.680.150.070.070.020.070.090.11−0.59−0.73−0.29⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤[12.4009.5][0.560.120.590−0.020.560.120.09−0.690.090−0.69]≈⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0.922.913.904.820.70−0.70.320.953.014.045.000.531.340.230.922.913.904.820.70−0.70.320.01−0.010.010.034.114.782.010.01−0.010.010.034.114.782.01⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
将截取下来的矩阵相乘,就低秩近似原来的数据矩阵,对比俩个矩阵可以发现,俩者数值非常接近。
- 原始矩阵: [ 1 1 1 0 0 3 3 3 0 0 4 4 4 0 0 5 5 5 0 0 0 2 0 4 4 0 0 0 5 5 0 1 0 2 2 ] \left[ \begin{matrix} 1 & 1 & 1 & 0 & 0 \\ 3 & 3 & 3 & 0 & 0 \\ 4 & 4 & 4 & 0 & 0 \\ 5 & 5 & 5 & 0 & 0 \\ 0 & 2 & 0 & 4 & 4 \\ 0 & 0 & 0 & 5 & 5 \\ 0 & 1 & 0 & 2 & 2 \end{matrix} \right] ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡13450001345201134500000004520000452⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤ 近似矩阵: [ 0.92 0.95 0.92 0.01 0.01 2.91 3.01 2.91 − 0.01 − 0.01 3.90 4.04 3.90 0.01 0.01 4.82 5.00 4.82 0.03 0.03 0.70 0.53 0.70 4.11 4.11 − 0.7 1.34 − 0.7 4.78 4.78 0.32 0.23 0.32 2.01 2.01 ] \left[ \begin{matrix} 0.92 & 0.95 & 0.92 & 0.01 & 0.01 \\ 2.91 & 3.01 & 2.91 & -0.01 & -0.01 \\ 3.90 & 4.04 & 3.90 & 0.01 & 0.01 \\ 4.82 & 5.00 & 4.82 & 0.03 & 0.03 \\ 0.70 & 0.53 & 0.70 & 4.11 & 4.11 \\ -0.7 & 1.34 & -0.7 & 4.78 & 4.78 \\ 0.32 & 0.23 & 0.32 & 2.01 & 2.01 \end{matrix} \right] ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0.922.913.904.820.70−0.70.320.953.014.045.000.531.340.230.922.913.904.820.70−0.70.320.01−0.010.010.034.114.782.010.01−0.010.010.034.114.782.01⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
工程应用:图像压缩
基于奇异值分解的【低秩近似】理论在工程中有广泛的应用,比如图像压缩。
图像本来就是一个矩阵,比如下面的图片:

假设这张图片的尺寸是 500 ∗ 395 500*395 500∗395,就需要 500 ∗ 395 500*395 500∗395 个字节来存储。
就这样一张不大的灰度图,都要将近 2 2 2 万字节( 20 K B 20KB 20KB)存储,要是某个应用是图片为主的,那您可以想象应用会有多大。
图像压缩主要有俩个好处:
- 存储空间会小很多
- 方便网络传输
我们可以用 奇异值分解 来压缩图像,算法就是【低秩近似】理论。
图像压缩有俩部分:
-
压缩图像
对 m ∗ n m*n m∗n 图像矩阵做奇异值分解,得到 U m ∗ m 、 ∑ m ∗ n 、 V n ∗ n T U_{m*m}、\sum_{m*n}、V^{T}_{n*n} Um∗m、∑m∗n、Vn∗nT
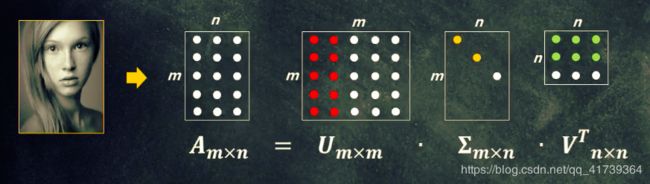
选取前 k k k 大的奇异值( k < = n k<=n k<=n),按照【低秩近似】理论,对 U m ∗ m 、 ∑ m ∗ n 、 V n ∗ n T U_{m*m}、\sum_{m*n}、V^{T}_{n*n} Um∗m、∑m∗n、Vn∗nT 做截取,得到 U m ∗ k 、 ∑ k ∗ k 、 V k ∗ n T U_{m*k}、\sum_{k*k}、V^{T}_{k*n} Um∗k、∑k∗k、Vk∗nT存储或者传输新的 U m ∗ k 、 ∑ k ∗ k 、 V k ∗ n T U_{m*k}、\sum_{k*k}、V^{T}_{k*n} Um∗k、∑k∗k、Vk∗nT,新的矩阵不一定比原来的小,一定要选取一个恰当的 k k k
-
图像重构
将 U m ∗ k 、 ∑ k ∗ k 、 V k ∗ n T U_{m*k}、\sum_{k*k}、V^{T}_{k*n} Um∗k、∑k∗k、Vk∗nT 按顺序乘起来,图像的主要信息就可以表示出来啦。但
完整代码:
import cv2
# cv 库用来读取图片
import numpy as np
import matplotlib.pyplot as plt
# plt 库显示图片
''' @para: c 是保留奇异值(奇异向量)个数占总个数比例 '''
def imgCompress(c, img):
# 1. 图像压缩(SVD), 返回的是分解后的 3 个矩阵
U, sigma, VT = np.linalg.svd(img)
k = int(c * img.shape[1]) # .shape[1] 是列数,也是奇异值的个数
sig = np.eye(k) * sigma[ :k] # sigma矩阵截取,构造新的奇异值矩阵,也是一个对角矩阵
# 2. 图像重构
res_img = (U[:, :k] * sig) * VT[:k, :] # U、VT矩阵截取,并相乘
size = U.shape[0] * k + sig.shape[0] * sig.shape[1] + k * VT.shape[1]
# 压缩后的数据量 = 截取后的(U的大小 + sigma的大小 + VT的大小)
return res_img, size;
if __name__ == '__main__':
# 1.读取待压缩的图像
img_path = input("图片路径:> ")
ori_img = np.mat(cv2.imread(img_path, cv2.IMREAD_GRAYSCALE)) # cv2.IMREAD_GRAYSCALE:以灰度图方式读取
# 2.图像压缩(含重构)
res_img, size = imgCompress(0.1, ori_img) # 0.1 只保留前 10% 的奇异值,比例越小,压缩的越厉害,重构的图片就越模糊
print("压缩前图像大小:> ", str(ori_img.shape[0] * ori_img.shape[1]))
print("压缩后图像大小:> ", str(size))
# 显示图像(对比)
fig, ax = plt.subplots(1, 2)
ax[0].imshow(ori_img, cmap='gray')
ax[0].set_title("before compress")
ax[1].imshow(res_img, cmap='gray')
ax[1].set_title("after compress")
plt.show()
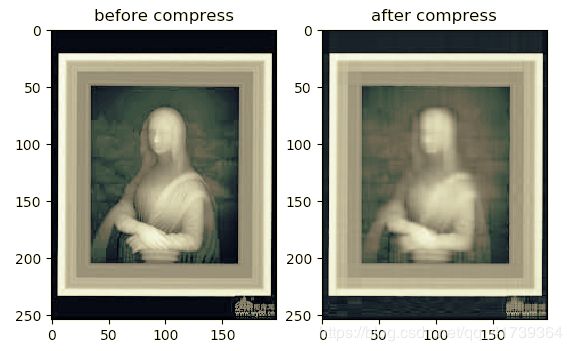
运行结果:
-
压缩前图像大小:> 50292 -
压缩后图像大小:> 8949哈哈,整整压缩了一个量级( 10 倍 10倍 10倍)。
显示图片:
工程应用:推荐系统
您看,我正在看电影,右边会有一个推荐列表。
TA这个是根据什么推荐呢?
可能是我根据的观看记录,这里我们以评分为判断依据吧,简单起见。
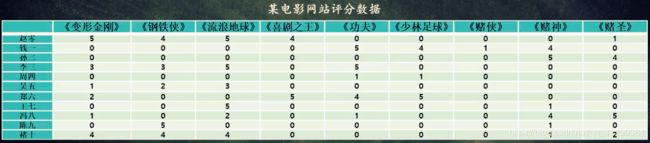
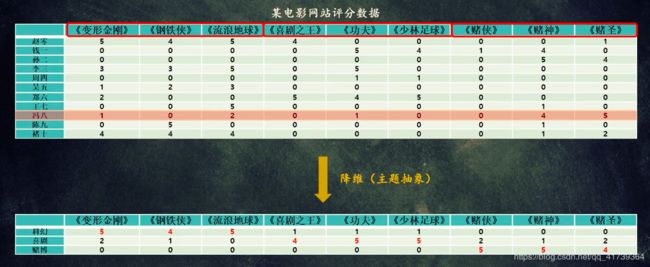
上图一共 11 11 11 位大佬,一共有 9 9 9 部电影,电影评分是 1 − 5 1-5 1−5, 0 0 0 表示未评分或者未看过。
现在【冯八】大佬又来看电影了,我们应该推荐什么给【冯八】呢?
因为每一部电影都有分类的,我们可以在一个类别里面给【冯八】挑:
- 科幻:变形金刚、钢铁侠、流浪地球
- 喜剧:喜剧之王、功夫、少林足球
- 赌博:赌侠、赌神、赌圣
【冯八】给赌博片的打分普遍很高(赌圣5分、赌神4分),所以应该推荐赌博片里没看过的赌侠。
不过计算机理解不了这个影片分类,所以我们可以使用降维,使得数据投影变成 3 3 3 维,就有了科幻、喜剧、赌博的分类。
介绍一下,推荐系统的流程:
- 前置准备,把所有用户的评分数据放入到一个矩阵里。
- 现在为【冯八】推送服务,寻找【冯八】未打分的电影 — 在这个矩阵的第九行里寻找等于 0 0 0 的元素。
-
预测【冯八】会给那些未打分的电影,打多少分。

科幻类(黄色)打 2 2 2 分,喜剧类(蓝色)打 2 2 2 分,赌博片(红色)打 4 4 4 分。这里的分类,其实是降维操作 — 使用 P C A PCA PCA 算法将高维投影低维。 P C A PCA PCA 算法可参考《特征值分解实验:人脸识别与PageRank网页排序》。不过,这里面的 P C A PCA PCA 算法采用的是特征值分解(EVD),这篇文章是奇异值分解(SVD),所以我们还是用奇异值分解包装的 P C A PCA PCA 算法。
奇异向量也可以构造 降维矩阵,因为我们现在是对行降维,协方差矩阵维是 A A T AA^{T} AAT,做奇异值分解时,左奇异矩阵 U U U 就是矩阵 A ∗ A T A*A^{T} A∗AT 的特征向量拼接而来的 — 所以说,奇异值分解的过程中,本身就包含了特征值分解。用特征值来构造降维矩阵,和用奇异向量构造降维矩阵其实是一回事,只是书写方式不同。
所以,我们使用 S V D SVD SVD 来构造降维矩阵,那降维矩阵就是从 左奇异矩阵 U U U 中截取: ( U m ∗ k ) T ⋅ A m ∗ n = B k ∗ n (U_{m*k})^{T}·A_{m*n}=B_{k*n} (Um∗k)T⋅Am∗n=Bk∗n。
因为 左奇异矩阵 U U U 是列向量横向堆叠而成的,所以要转置一下。而后将 数据矩阵 A A A 投影到 U U U 所代表的低维空间里,得到矩阵 B B B。
如果是对行降维,协方差矩阵维是 A A T AA^{T} AAT,降维矩阵从左奇异矩阵 U U U 中截取: ( U m ∗ k ) T ⋅ A m ∗ n = B k ∗ n (U_{m*k})^{T}·A_{m*n}=B_{k*n} (Um∗k)T⋅Am∗n=Bk∗n。
如果是对列降维,协方差矩阵维是 A T A A^{T}A ATA,降维矩阵从右奇异矩阵 V T V^{T} VT 中截取: ( V k ∗ n T ) T ⋅ A m ∗ n = B m ∗ k (V^{T}_{k*n})^{T}·A_{m*n}=B_{m*k} (Vk∗nT)T⋅Am∗n=Bm∗k。
在低维空间中,计算出待预测电影与其他电影的相似度。计算相似度,采用相似度算法接口,可参考《向量实验:相似度算法》。
而后,逐一将已评分电影的分数 ∗ * ∗ 相似度,而后求和 — 把相似度当成权重,得到预测分数
-
根据预测评分的大小排序,就前 N N N 个电影给用户。
import numpy as np
def load_dataSet(): # “用户-电影”矩阵 ,行表示用户的评分 ,列表示电影
return np.mat([ [ 5, 4, 5, 4, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 5, 4, 1, 4, 0],
[0, 0, 0, 0, 0, 0, 0, 5, 4],
[3, 3, 5, 0, 5, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 1, 0, 0, 0],
[1, 2, 3, 0, 0, 0, 0, 0, 0],
[2, 0, 0, 5, 4, 5, 0, 0, 0],
[0, 0, 5, 0, 0, 0, 0, 1, 0],
[1, 0, 2, 0, 1, 0, 0, 4, 5],
[0, 5, 0, 0, 0, 0, 0, 1, 0],
[4, 4, 4, 0, 0, 0, 0, 1, 2]])
def cosSim(inA, inB):
return 0.5 + 0.5 * (float(inA.T * inB) / (np.linalg.norm(inA) * np.linalg.norm(inB))) # 归一化到[0,1],配合分数的归一化
def scorePredict(dataMat, xformedItems, user_id, unrated_idx):
rateTotal = 0.0 # 预测分数
simTotal = 0.0 # 总相似度(权重)
n = dataMat.shape[1] # 获取电影个数
for i in range(n): # 遍历所有电影
userRating = dataMat[user_id, i] # 针对该用户,拿到一个电影得分 [1, 0, 2, 0, 1, 0, 0, 4, 5],
if userRating == 0 : # 跳过未评分项
continue
similarity = cosSim(xformedItems[:, unrated_idx], xformedItems[:, i]) # 求余弦相似度
print( 'the movie_%d and movie_%d similarity is: %f' % (unrated_idx, i, similarity))
rateTotal += similarity * userRating # 预测分数 = 相似度 * 已评分数
simTotal += similarity # 相似度求和
return rateTotal / simTotal # 评分归一化:使得评分值在0-5之间
def recommed(dataMat,user_id,N=3):
# 1. 找出该用户未评分电影
unratedItems = np.nonzero(dataMat[user_id, :]==0)[1] # “==0”操作将0置为1,将非0置为0 [0, 1, 0, 1, 0, 1, 1, 0, 0]
print("-------- The user -------\n",np.around(dataMat[user_id, :], decimals=3))
print("-------- unratedItems -------\n",np.around(unratedItems , decimals=3))
# 2.预测评分
# 2.1. 降维(提取电影主题)
U, Sigma, VT = np.linalg.svd(dataMat)
# U*U.T = E ?若为E证明U为正交矩阵,其列向量已经单位正交化,就不用像EVD降维那样,还要自己单位化
print("----- U*U.T = E ? -----\n",np.around(U*U.T, decimals=0))
# 2.2 自动收缩最适合的k
k = 0
for i in range(len(Sigma)):
if (np.linalg.norm(Sigma[:i + 1]) / np.linalg.norm(Sigma)) > 0.9:
k = i + 1
break #刚好找到满足条件的k,退出循环
# 2.3 截取U,得到降维矩阵
red_U = U[:, :k]
# 2.4 降维
xformedItems = red_U.T * dataMat
print("xformedItems shape:",xformedItems.shape) # (3, 9)
print("----- xformedItems -----\n",np.around(xformedItems, decimals=2))
# 2.5 对未评分电影逐一进行分数预测
movScores = [] # 存储预测到的分数
for unrated_idx in unratedItems: # 遍历所有未评分项的索引,逐项预测
print ("-------- predict movie_%d -------" % (unrated_idx))
score = scorePredict(dataMat, xformedItems, user_id, unrated_idx) # 预测当前未评分项的分数
movScores.append((unrated_idx, score)) # 以元组方式堆叠到movScores
print("-------- movScores -------\n",np.around(movScores, decimals=3))
# 3.按照预测分数从大到小排序,并返回前N大分数对应的电影
return sorted(movScores, key=lambda tmp: tmp[1], reverse=True)[:N]
if __name__ == "__main__":
# 1.加载数据集
dataMat = load_dataSet()
print("dataMat shape:",dataMat.shape)
print("-------- dataMat -------\n",np.around(dataMat, decimals=3))
# 2.输入一个用户编号,给他推荐N部电影
user_id = 8
N = 4
recommed_items = recommed(dataMat,user_id,N)
print("---the recommendation of our system for user_%d are as follows---"%(user_id))
print(np.around(recommed_items, decimals=3))
print("done!!!!")
就我们设计的推荐系统,可能面临的一些问题:
-
可能会有上亿用户,数据矩阵规模很大,矩阵分解会很耗时间;
解决:因为这个矩阵在一段时间之内变换不大,所以一般一天计算一次就好。
-
电影有成千上万部,需要多次计算相似度,也很耗时间;
解决:提前计算各个电影直接的相似度,需要的时候调用即可,不用计算。
-
很多用户都没有给电影打分的习惯,所以矩阵爆 0 0 0,会影响推荐效果。
解决:胡歌,请您来打分~