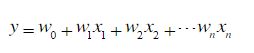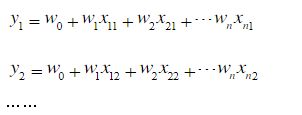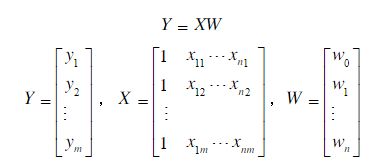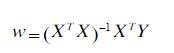陈一月的编程岁月

基于jupyter notebook的python编程-----通过矩阵实现最小二乘法对求多元线性回归方程的的待定系数a和判定系数R2的求解

基于jupyter notebook的python编程-----通过矩阵实现最小二乘法对多元线性回归方程的的待定系数a和判定系数R2的求解目录

一、二元线性回归的推导原理

1、因变量y关于自标量x1、x2、x3、xn的多元回归方程如下：
2、离散化数据（m组离散化数据）代入、可得：
3、转化为矩阵形式如下
4、矩阵形式变形为：
5、所以，通过如上步骤，我们就可以得到系数矩阵W

二、运行jupyter notebook，搭建python环境

1、打开Windows终端命令行，输入jupyter notebook，打开我们的jupyter工具，如下所示：
2、在jupyter的web网页中创建python文件，如下所示：
3、现在就可以在jupyter的代码行里面输入我们的代码啦！

三、多元线性回归例题[店铺营业额-店铺面积-离车站距离]的数据如下

1、用于矩阵推导的数据如下：
2、用于模拟线性回归的曲线图的数据如下：

四、python编程进行推导解析

1、导入本次例题所需要的库
2、通过导入的数据，对我们的自变量X1、X2和因变量Y赋值
3、通过原理，需要将自变量X1、X2，因变量Y的值转换为矩阵模式
4、求解判定系数R2
5、通过上述步骤的求解，整理，求解判定系数R2

五、该例题的python源码
六、整体的运行结果如下：
七、对比我们Excel逐步求解的结果

1、对比Excel的求解的结果如下所示：

上次博客，林君学长介绍了如何通过线性回归的求解原理，利用python一步一步进行推导，求解一元线性回归的的待定系数a和判定系数R2,那么面的多元线性回归的待定系数及断定系数，我们又如何通过原理进行求解呢？这就是本次博客的内容
本次博客，通过例题店铺营业额-店铺面积-离车站距离等”多元线性回归的参数求解，来理解如何通过原理进行推导

一、二元线性回归的推导原理

1、因变量y关于自标量x1、x2、x3、xn的多元回归方程如下：

其中，w0，w1，w2，Wn,为回归系数

2、离散化数据（m组离散化数据）代入、可得：

3、转化为矩阵形式如下

4、矩阵形式变形为：

5、所以，通过如上步骤，我们就可以得到系数矩阵W

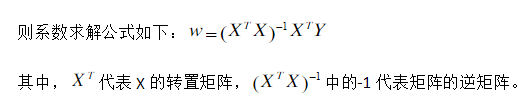
上面的步骤就是对多元线性回归方程的系数求解的实验原理，接下来，就让我们通过python代码进行推导过程的模拟吧！

二、运行jupyter notebook，搭建python环境

1、打开Windows终端命令行，输入jupyter notebook，打开我们的jupyter工具，如下所示：

2、在jupyter的web网页中创建python文件，如下所示：

3、现在就可以在jupyter的代码行里面输入我们的代码啦！

三、多元线性回归例题[店铺营业额-店铺面积-离车站距离]的数据如下

1、用于矩阵推导的数据如下：

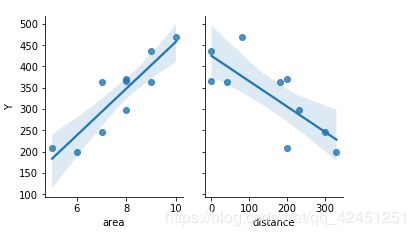
2、用于模拟线性回归的曲线图的数据如下：

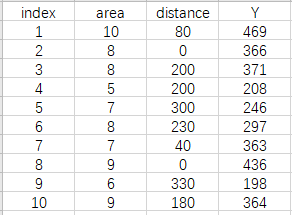
可以看到，上面数据的内容是一样的，只不过保存的数据格式不一样，这是因为我编写代码导入的数据的包用的不一样的，所以自己对同一个数据建立了两个不同的表格，虽然繁琐，但是有用哦！index项不用管，可以不要，只要用来表示序号的！

四、python编程进行推导解析

1、导入本次例题所需要的库

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
%matplotlib inline

numpy库用来做矩阵运算的
pandas库用来导入表格数据文件的
matplotlib库用来画拟合回归曲线图的
seaborn库是matplotlib的子库，本次的置信带的图就是这个库的功劳哦
没有这个库的小伙伴可以在python命令行中输入以下命令进行下载：

pip install seaborn

2、通过导入的数据，对我们的自变量X1、X2和因变量Y赋值

data = np.genfromtxt("D:/面积距离车站数据.csv",delimiter=",")
X1=data[0:10,0]#自变量温度
X2=data[0:10,1]#因变量销售量
Y=data[0:10,2]#自变量温度

3、通过原理，需要将自变量X1、X2，因变量Y的值转换为矩阵模式

1）、原理如下：

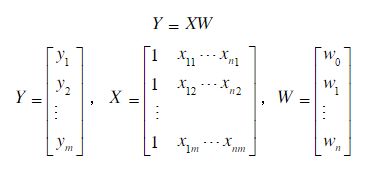
2）、因变量（月销售额）Y进行矩阵化的代码：

#将因变量赋值给矩阵Y1
Y1=np.array([Y]).T

3）、自变量X1（店铺面积0）、X2（距离车站的距离）、进行矩阵化变为原理的X矩阵的代码：

#为自变量系数矩阵X赋值
X11=np.array([X1]).T
X22=np.array([X2]).T
A=np.array([[1],[1],[1],[1],[1],[1],[1],[1],[1],[1]])#创建系数矩阵
B=np.hstack((A,X11))#将矩阵a与矩阵X11合并为矩阵b
X=np.hstack((B,X22))#将矩阵b与矩阵X22合并为矩阵X

4）、求X矩阵的转置矩阵==X_==矩阵

#求矩阵X的转置矩阵
X_=X.T

5）、求矩阵X与他的==转置矩阵的X_==的乘积

X_X=np.dot(X_,X)

6）、求矩阵X与他的转置矩阵的X_的乘积的逆矩阵
及求下面红色圈中的部分：

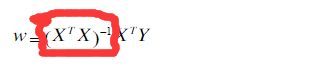
X_X_=np.linalg.inv(X_X)

7）、求解系数矩阵W

#求解系数矩阵W，分别对应截距b、a1、和a2
W=np.dot(np.dot((X_X_),(X_)),Y1)

8）、将系数矩阵W转换为系数a1、a2和截距b，并输入线性回归方程

b=W[0][0]
a1=W[1][0]
a2=W[2][0]
print("系数a1=",a1)
print("系数a2=",a2)
print("截距为=",b)
print("多元线性回归方程为:y=",a1,"X1+",a2,"X2+",b)

运行结果如下：

9）、画出线性回归分析图

data1=pd.read_excel('D:\面积距离车站数据.xlsx')
sns.pairplot(data1, x_vars=['area','distance'], y_vars='Y', height=3, aspect=0.8, kind='reg')  
plt.show()

运行结果如下：

4、求解判定系数R2

判定系数R2如何求？就只有通过他的表达式来进行求解啦，R2的表达式如下所示：

及R2=R*R，也就是说，我们需要求解Syy、Syy1、以及Sy1y1,分别代表什么含义上面的公式已经给出了哦，下面、就让我们一起来进行求解吧！
1）、求解月销售额的总值，以及平均值y1

#求月销售量Y的和以及平均值y1
sumy=0#因变量的和
y1=0#因变量的平均值
for i in range(0,len(Y)):
    sumy=sumy+Y[i]
y1=sumy/len(Y)

2）、求解月销售额y减去它平均值的和y_y1

#求月销售额y-他的平均值的和
y_y1=0#y-y1的值的和
for i in range(0,len(Y)):
    y_y1=y_y1+(Y[i]-y1)
print("销售量-销售量平均值的和为:",y_y1)

运行结果如下：

3）、通过上面系数和截距，求出预测的月销售额sales1

sales1=a1x1+a2x2+b

#求预测值sales1
sales1=[]
for i in range(0,len(Y)):
    sales1.append(a1*X1[i]+a2*X2[i]+b)

4）、求预测月销售额的平均值y2

#求预测值的平均值y2
y2=0
sumy2=0
for i in range(len(sales1)):
    sumy2=sumy2+sales1[i]
y2=sumy2/len(sales1)

5)、求预测月销售额减去其平均值的和y11_y2

#求预测值-平均值的和y11_y2
y11_y2=0
for i in range(0,len(sales1)):
   y11_y2=y11_y2+(sales1[i]-y2)
print("预测销售值-预测销售平均值的和为:",y11_y2)

运行结果如下：

6）、求月销售额y减去他的平均值的平方和Syy

#求月销售额y-他的平均值的平方和
Syy=0#y-y1的值的平方和
for i in range(0,len(Y)):
    Syy=Syy+((Y[i]-y1)*(Y[i]-y1))
print("Syy=",Syy)

运行结果如下：

7）、求预测月销售额减去其平均的平方和Sy1y1

#求y1-y1平均的平方和
Sy1y1=0
for i in range(0,len(sales1)):
    Sy1y1=Sy1y1+((sales1[i]-y2)*(sales1[i]-y2))
print("Sy1y1=",Sy1y1)

运行结果如下：

8）、求（y1-y1平均）*（y-y平均）的和Syy1

#（y1-y1平均）*（y-y平均）
Syy1=0
for i in range(0,len(sales1)):
    Syy1=Syy1+((Y[i]-y1)*(sales1[i]-y2))
print("Syy1=",Syy1)