稳定排序与不稳定排序(插入, 冒泡, 归并, 选择, 快速)排序
内部排序与外部排序
内部排序:只用到了电脑内存而不使用外存的排序方式
外部排序:同时动用了电脑内存和外存的排序方式
稳定排序与不稳定排序
通俗地讲就是能保证排序前两个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。在简单形式化一下,如果Ai = Aj,Ai原来在位置前,排序后Ai还是要在Aj位置前。
在本篇博客中
稳定排序:插入排序, 冒泡排序, 归并排序
不稳定排序:选择排序, 快速排序
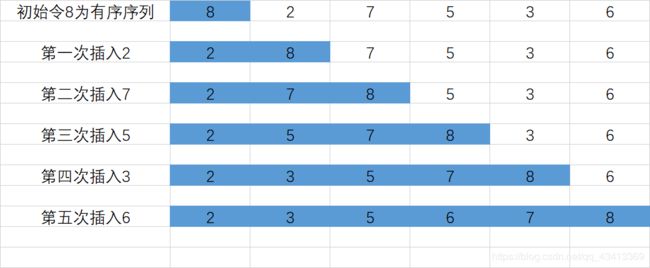
插入排序
(内部排序)
在添加新的记录时,使用顺序查找的方式找到其要插入的位置,然后将新记录插入。
void insert(int* num, int n) {
for (int i = 1; i < n; i++) {
for (int j = i; j > 0 && num[j] < num[j - 1]; j--) {
swap(num[j], num[j - 1]);
}
}
return;
}
时间复杂度为O(n^2)
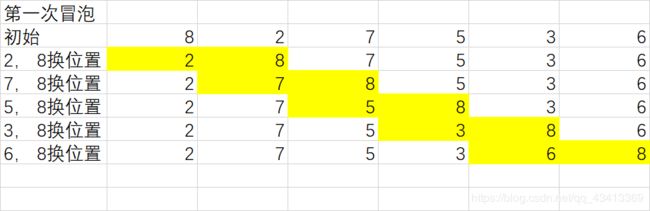
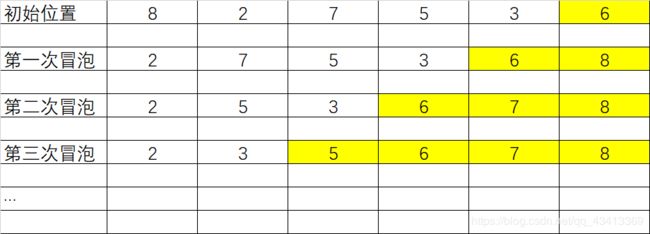
冒泡排序
(内部排序)
每两两交换一次位置, 比如说第一次冒泡
时间复杂度为O(n^2)
void bubble_sort(int* num, int n) {
for (int i = 1; i < n && times; i++) {
for (int j = 0; j < n - i; j++) {
if (num[j] <= num[j + 1]) continue;
swap(num[j], num[j + 1]);
}
}
return;
}
第三轮开始可以优化
void bubble_sort(int* num, int n) {
int times = 1;
for (int i = 1; i < n && times; i++) {
times = 0;
for (int j = 0; j < n - i; j++) {
if (num[j] <= num[j + 1]) continue;
swap(num[j], num[j + 1]);
times++;
}
}
return;
}
归并排序
(外部排序)
将问题分成一些小的问题然后递归求解,将分的阶段得到的各答案合在一起

void merge_sort(int* num, int l, int r) {
if (r - l <= 1) {
if (r - l == 1 && num[l] > num[r]) {
swap(num[l], num[r]);
}
return;
}
int mid = (l + r) >> 1;
merge_sort(num, l, mid);
merge_sort(num, mid + 1, r);
int* temp = (int*)malloc(sizeof(int) * (r - l + 1));
int p1 = l, p2 = mid + 1, k = 0;
while (p1 <= mid || p2 <= r) {
if (p2 > r || (p1 <= mid && num[p1] <= num[p2])) {
temp[k++] = num[p1++];
} else {
temp[k++] = num[p2++];
}
}
memcpy(num + l, temp, sizeof(int) * (r - l + 1));
free(temp);
return;
}
选择排序
(不稳定排序)
选择排序,从头至尾扫描序列,找出最小的一个元素,和第一个元素交换,接着从剩下的元素中继续这种选择和交换方式,最终得到一个有序序列
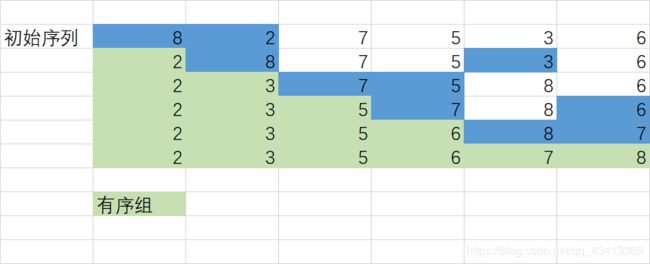
void select_sort(int *num, int n) {
for (int i = 0; i < n - 1; i++) {
int ind = i;
for (int j = i + 1; j < n; j++) {
if (num[ind] > num[j]) ind = j;
}
swap(num[i], num[ind]);
}
return ;
}
时间复杂度O(n^2)
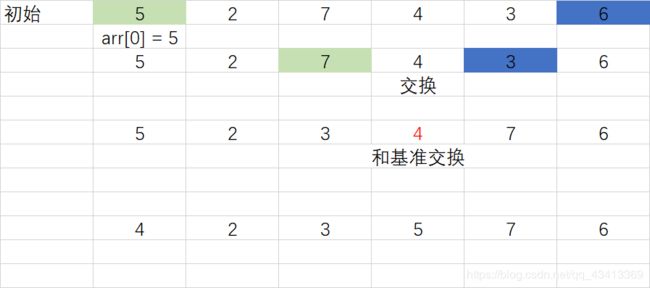
快速排序
其基本思想是随机找出一个数(通常就拿数组第一个数据就行),把它插入一个位置,使得它左边的数都比它小,它右边的数据都比它大,这样就将一个数组分成了两个子数组,然后再按照同样的方法把子数组再分成更小的子数组,直到不能分解为止。
//只适用于无重复数字的数组
void quick_sort(int *num, int l, int r) {
int x = l, y = r, z = num[l];
if (x < y) return ;
while (x < y) {
while (x < y && num[y] >= z) y--;
while (x < y && num[x] <= z) x++;
if (x < y) swap(num[x], num[y]);
}
swap(num[l], num[x]);
quick_sort(num, l, x - 1);
quick_sort(num, x + 1, r);
return ;
}
优化
//都可
void quick_sort(int *num, int l, int r) {
while (l < r) {
int x = l, y = r, z = num[(l + r) >> 1];
do {
while (x <= y && num[x] < z) x++;
while (x <= y && num[y] > z) y--;
if (x <= y) {
swap(num[x], num[y]);
x++, y--;
}
} while (x <= y);
quick_sort(num, x, r);
r = y;
}
return ;
}
时间复杂度O(nlogn)