集成学习之Bagging与随机森林算法原理小结
在集成学习原理小结中,我们讲到了集成学习有两个流派,一个是boosting派系,它的特点是各个弱学习器之间有依赖关系。另一种是bagging流派,它的特点是各个弱学习器之间没有依赖关系,可以并行拟合。本文就对集成学习中Bagging与随机森林算法做一个总结。
随机森林是集成学习中可以和梯度提升树GBDT分庭抗礼的算法,尤其是它可以很方便的并行训练。
一、bagging原理
在集成学习原理小结中,Bagging的原理图如下
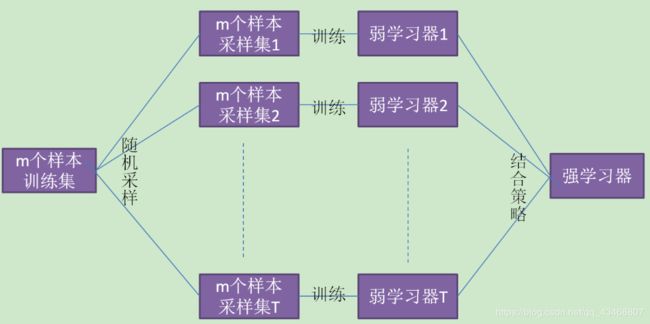
从上图可以看出,Bagging的弱学习器之间的确没有boosting那样的联系,它的特点在“随机采样”。
随机采样(bootsrap)就是从我们的训练集里面采集固定个数的样本,但是每采集一个样本后,都将样本放回。也就是说,之前采集到的样本在放回后有可能继续被采集到。对于我们的Bagging算法,一般会随机采集和训练集样本数m一样个数的样本。这样得到的采样集和训练集样本的个数相同,但是样本内容不同。如果我们对有m个样本训练集做T次的随机采样,,则由于随机性,T个采样集各不相同。
这和GBDT的子采样是不同的。GBDT的子采样是无放回采样,而Bagging的子采样是放回采样。
对于一个样本,它在某一次含m个样本的训练集的随机采样中,每次被采集到的概率是1m。不被采集到的概率为 1 − 1 m 1−\frac{1}{m} 1−m1 。如果 m m m 次采样都没有被采集中的概率是 ( 1 − 1 m ) m (1−\frac{1}{m})m (1−m1)m。当 m → ∞ m→∞ m→∞ 时, ( 1 − 1 m ) m → 1 e ≃ 0.368 (1−\frac{1}{m})m→1e≃0.368 (1−m1)m→1e≃0.368。也就是说,在bagging的每轮随机采样中,训练集中大约有36.8%的数据没有被采样集采集中。
对于这部分大约36.8%的没有被采样到的数据,我们常常称之为袋外数据(Out Of Bag, 简称OOB)。这些数据没有参与训练集模型的拟合,因此可以用来检测模型的泛化能力。
bagging对于弱学习器没有限制,这和Adaboost一样。但是最常用的一般也是决策树和神经网络。
bagging的集合策略也比较简单,对于分类问题,通常使用简单投票法,得到最多票数的类别或者类别之一为最终的模型输出。对于回归问题,通常使用简单平均法,对T个弱学习器得到的回归结果进行算术平均得到最终的模型输出。
由于Bagging算法每次都进行采样来训练模型,因此泛化能力很强,对于降低模型的方差很有作用。当然对于训练集的拟合程度就会差一些,也就是模型的偏倚会大一些。
二、bagging算法流程
上一节我们对bagging算法的原理做了总结,这里就对bagging算法的流程做一个总结。相对于Boosting系列的Adaboost和GBDT,bagging算法要简单的多。
输入为样本集 D = ( x , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) D={(x,y_1),(x_2,y_2),...,(x_m,y_m)} D=(x,y1),(x2,y2),...,(xm,ym),弱学习器算法, 弱分类器迭代次数 T。
输出为最终的强分类器 f ( x ) f(x) f(x)
- 对于 t = 1 , 2... , T : t=1,2...,T: t=1,2...,T:
1.1 对训练集进行第t次随机采样,共采集m次,得到包含m个样本的采样集 D t D_t Dt 。
1.2 用采样集 D t D_t Dt 训练第t个弱学习器 G t ( x ) G_t(x) Gt(x) 。 - 如果是分类算法预测,则T个弱学习器投出最多票数的类别或者类别之一为最终类别。如果是回归算法,T个弱学习器得到的回归结果进行算术平均得到的值为最终的模型输出。
三、随机森林算法
随机森林(Random Forest,以下简称RF)是Bagging算法的进化版,也就是说,它的思想仍然是bagging,但是进行了独有的改进。
首先,RF使用了CART决策树作为弱学习器,这让我们想到了梯度提升树GBDT。第二,在使用决策树的基础上,RF对决策树的建立做了改进,对于普通的决策树,会在节点上所有的n个样本特征中选择一个最优的特征来做决策树的左右子树划分,但是RF通过随机选择节点上的一部分样本特征,这个数字小于n,假设为 n s u b n_{sub} nsub,然后在这些随机选择的 n s u b n_{sub} nsub 个样本特征中,选择一个最优的特征来做决策树的左右子树划分。这样进一步增强了模型的泛化能力。
如果 n s u b = n n_{sub}=n nsub=n,则此时RF的CART决策树和普通的CART决策树没有区别。 n s u b n_{sub} nsub 越小,则模型约健壮,当然此时对于训练集的拟合程度会变差。也就是说 n s u b n_{sub} nsub 越小,模型的方差会减小,但是偏倚会增大。在实际案例中,一般会通过交叉验证调参获取一个合适的 n s u b n_{sub} nsub 的值。
除了上面两点,RF和普通的bagging算法没有什么不同, 下面简单总结下RF的算法。
输入为样本集 D = ( x , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) D={(x,y_1),(x_2,y_2),...,(x_m,y_m)} D=(x,y1),(x2,y2),...,(xm,ym), 弱分类器迭代次数 T。
输出为最终的强分类器 f ( x ) f(x) f(x)
- 对于 t = 1 , 2... , T : t=1,2...,T: t=1,2...,T:
1.1 对训练集进行第t次随机采样,共采集m次,得到包含m个样本的采样集 D t D_t Dt 。
1.2 用采样集 D t D_t Dt 训练第t个决策树模型 G t ( x ) G_t(x) Gt(x),在训练决策树模型的节点的时候, 在节点上所有的样本特征中选择一部分样本特征, 在这些随机选择的部分样本特征中选择一个最优的特征来做决策树的左右子树划分 。 - 如果是分类算法预测,则T个弱学习器投出最多票数的类别或者类别之一为最终类别。如果是回归算法,T个弱学习器得到的回归结果进行算术平均得到的值为最终的模型输出。
四、随机森林小结
RF的主要优点有:
- 训练可以高度并行化,对于大数据时代的大样本训练速度有优势。个人觉得这是的最主要的优点。
- 由于可以随机选择决策树节点划分特征,这样在样本特征维度很高的时候,仍然能高效的训练模型。
- 在训练后,可以给出各个特征对于输出的重要性。
- 由于采用了随机采样,训练出的模型的方差小,泛化能力强。
- 相对于Boosting系列的Adaboost和GBDT, RF实现比较简单。
- 对部分特征缺失不敏感。
RF的主要缺点有:
- 在某些噪音比较大的样本集上,RF模型容易陷入过拟合。
- 取值划分比较多的特征容易对RF的决策产生更大的影响,从而影响拟合的模型的效果。