《机器学习》周志华(西瓜书)学习笔记 第九章 聚类

机器学习笔记

总目录

第九章 聚类

聚类是一种经典的无监督学习方法，无监督学习的目标是通过对无标记训练样本的学习，发掘和揭示数据集本身潜在的结构与规律，即不依赖于训练数据集的类标记信息。聚类则是试图将数据集的样本划分为若干个互不相交的类簇，从而每个簇对应一个潜在的类别。

9.1 距离度量

聚类性能度量亦称聚类"有效性指标" (validity index).

目标: 聚类结果的"簇内相似 度" (intra-cluster similarity)高且"簇间相似度" (inter-cluster similarity)低.

聚类性能度量大致有两类.

1. 一类是将聚类结果与某个"参考模 型" (reference model)进行比较，称为"外部指标" (external i丑dex)。
2. 另一 类是直接考察聚类结果而不利用任何参考模型，称为"内部指标" (internal index).

基于上图中得公式可以导出下面这些常用的聚类性能度量外部指标：


基于上图中的公式可以到处下面这些常用的聚类度量内部指标：

9.2 距离计算

最常用的距离度量方法是“闵可夫斯基距离”（Minkowski distance)：

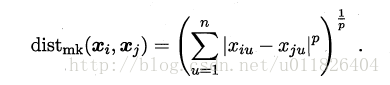
当p=1时，闵可夫斯基距离即曼哈顿距离（Manhattan distance）：

当p=2时，闵可夫斯基距离即欧氏距离（Euclidean distance）：

我们常将属性划分为"连续属性" (continuous attribute)和"离散属 性" (categorical attribute)，前者在定义域上有无穷多个可能的取值，后者在定 义域上是有限个取值.

• 若属性值之间存在序关系，则可以将其转化为连续值，例如：身高属性“高”“中等”“矮”，可转化为{1, 0.5, 0}。
• 若属性值之间不存在序关系，则通常将其转化为向量的形式，例如：性别属性“男”“女”，可转化为{（1,0），（0,1）}。

对于无序属性，我们一般采用VDM进行距离的计算.

令 $m_{u,a}$表示在属性 u 上取值为 α 的样本数， $m_{u,a,i}$ 表示在第 4 个样本簇 中在属性 u 上取值为 α 的样本数， k 为样本簇数，则属性 u 上两个离散值 α 与 b 之间的 VDM 距离为:

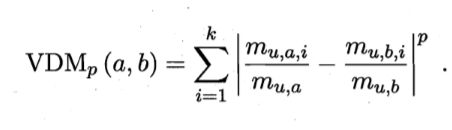
于是，将闵可夫斯基距离和 VDM 结合即可处理混合属性.假定有 $n_c$ 个有 序属性、 $n-n_c$ 个无序属性,不失一般性，令有序属性排列在无序属性之前，则:

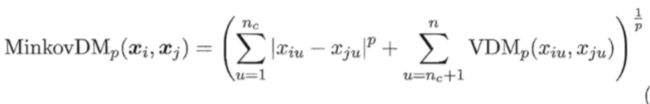
当样本空间中不 同属性的重要性不同时，可使用"加权距离" (weighted distance). 以加权闵可夫斯基距离为例:

9.3 原型聚类

原型聚类亦称"基于原型的聚类" (prototype~ based clustering)) 此类算法 假设聚类结构能通过一组原型刻画，在现实聚类任务中极为常用.通常情形下， 算法先对原型进行初始化，然后对原型进行迭代更新求解.采用不同的原型表 示、不同的求解方式?将产生不同的算法.T面介绍几种著名的原型聚类算法

9.3.1 K均值算法

K-Means的思想十分简单，首先随机指定类中心，根据样本与类中心的远近划分类簇，接着重新计算类中心，迭代直至收敛。但是其中迭代的过程并不是主观地想象得出，事实上，若将样本的类别看做为“隐变量”（latent variable），类中心看作样本的分布参数，这一过程正是通过EM算法的两步走策略而计算出，其根本的目的是为了最小化平方误差函数E：
$$E=\sum _{i=1}^k\sum _{xϵC_i}||x-u_i|{|}_2^2$$

其中 $u_i=\frac{1}{|C_i|}{\sum }_{xϵC_i}x$是簇$C_i$的均值向量

直观来看，上式在一定程度上 刻画了簇内样本围绕簇均值向量的紧密程度， E 值越小则簇内样本相似度越高.

K-Means的算法流程如下所示：

9.3.2 学习向量量化

LVQ也是基于原型的聚类算法，与K-Means不同的是，LVQ使用样本真实类标记辅助聚类，首先LVQ根据样本的类标记，从各类中分别随机选出一个样本作为该类簇的原型，从而组成了一个原型特征向量组，接着从样本集中随机挑选一个样本，计算其与原型向量组中每个向量的距离，并选取距离最小的原型向量所在的类簇作为它的划分结果，再与真实类标比较。

算法流程如下：

算法停止条件：
己达到最大迭代轮数，或原型向量更新很小甚至不再更新

9.3.3 高斯混合聚类

与 k 均值、 LVQ 用原型向量来刻画聚类结构不同，高斯混合(Mixture-oι Gaussian)聚类采用概率模型来表达聚类原型.

多维高斯分布该路密度函数：

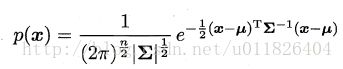
其中u表示均值向量，∑表示协方差矩阵，可以看出一个多维高斯分布完全由这两个参数所确定。接着定义高斯混合分布为：

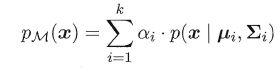
该分布共由 k 个混合成分组成，每个混合成分对应一个高斯分布. 其中$u_i$与${\sum }_i$是第 $i$个高斯混合成分的参数， 而 ${\alpha }_i>0$ 为相应的"混合系数"(mixture coefficient) ，${\sum }_{i=1}^k{\alpha }_i=1$

算法流程

9.3.4 密度聚类

密度聚类亦称"基于密度的聚类" (density-based clustering)，此类算法假 设聚类结构能通过样本分布的紧密程度确定.通常情形下，密度聚类算法从样 本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇 以获得最终的聚类结果.

DBSCAN 是一种著君的密度粟类算法?它基于一组"邻域" (neighborhood) 参数 $(ϵ，MinPts)$ 来刻画样本分布的紧密程度.给定数据集 $D=\{x_1，x_2，...，x_m\}$， 定义下面这几个概念:

算法流程：

9.3.5 层次聚类

层次聚类(hierarchical clustering)试图在不同层次对数据集进行划分，从而 形成树形的聚类结构. 数据集的划分可采用"自底向上"的聚合策略，也可采 用 “自顶向下” 的分拆策略.
AGNES 是一种采用自底向上聚合策略的层次聚类算法.它先将数据集中 的每个样本看作一个初始聚类簇，然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并，该过程不断重复，直至达到预设的聚类簇个数.这里的关 键是如何计算聚类簇之间的距离.实际上7 每个簇是一个样本集合，因此，只需 采用关于集合的某种距离即可.例如，给定聚类簇 $c_i与c_j$，可通过下面的式子 来计算距离:

显然,最小距离由两个簇的最近样本决定，最大距离由两个簇的最远样本决定7,而平均距离则由两个簇的所有样本共同决定.当聚类簇距离由 $d_{min},d_{max}或d_{avg}$ 计算时， AGNES 算法被相应地称为"单链接" (single-linkage)、 “全链 接” (complete-linkage) 或"均链接" (average-linkage)算法.