哈夫曼树应用——文件压缩
1.哈夫曼树的简介:
哈夫曼树(Huffman tree),又名最优树,指给定n个权值作为n的叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。
2.哈夫曼树的构造方式如下:
比如说有一组数,1,4,3,5,2,6,7,根据哈夫曼树的定义,首先我们找到这些树中最小的2个数据,当做叶子节点,用他们两个来构造其父亲节点,父亲节点的值即为2个叶子节点的权值之和,再将父亲放回原来的数据中,挑选出2个最小的来继续构建,依次类推,直到所有的数据都被拿出来我们构造他如下图所示:

每次都从数据中拿出2个最小的数据出来,但是要怎样才能拿出来最小的2个数据呢?这就要用到我之前介绍的堆,堆有最小堆 和最大堆,这里的哈夫曼树要运用最小堆的形式,把这些数据建立小堆,每次从中拿一个最小的,拿2次,构建哈夫曼树。
堆的实现代码前边我已经解释过,这里再看一遍实现的代码:
#pragma once
#include >
class Heap
{
public:
Heap()
{}
Heap(T* a, size_t sz)
{
for (int i = 0; i < sz; i++)
{
_a.push_back(a[i]);
}
//从最后一个叶节点的父节点建堆
for (int i = (sz - 2) / 2; i >= 0; --i)
{
_AdjustDown(i);
}
}
void Push(const T& x)
{
_a.push_back(x);
_AdjustUp(_a.size()-1);
}
void Pop()
{
assert(_a.size());
swap(_a[0], _a[_a.size() - 1]);
_a.pop_back();
_AdjustDown(0);
}
const T& Top()
{
return _a[0];
}
size_t Size()
{
return _a.size();
}
bool Empty()
{
return _a.empty();
}
protected:
void _AdjustDown(int parent)
{
int child = parent * 2 + 1;
int size = _a.size();
Compare com;
while (child < size)
{
if (child + 1 < size&&com(_a[child + 1], _a[child]))
{
++child;
}
if (com(_a[child], _a[parent]))
{
swap(_a[child], _a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void _AdjustUp(int child)
{
int parent = (child - 1) / 2;
Compare com;
while (child >= 0)
{//只考虑父亲与孩子的大小,不考虑兄弟之间大小
if (com(_a[child], _a[parent]))
{
std::swap(_a[child],_a[parent]);
child = parent;
parent =(child - 1) / 2;
}
else
{
break;
}
}
}
protected:
vector 接下来是生成哈夫曼树的代码,运用到了堆的问题
#pragma once
#include T>
struct HuffmanTreeNode
{
T _weight;
HuffmanTreeNode* _parent;
HuffmanTreeNode* _left;
HuffmanTreeNode* _right;
HuffmanTreeNode(const T& weight)
:_weight(weight)
, _parent(NULL)
, _left(NULL)
, _right(NULL)
{}
};
templateT>
class HuffmanTree
{
typedef HuffmanTreeNode<T> Node;
public:
HuffmanTree()
:_root(NULL)
{}
HuffmanTree(T* a, size_t size, T& invalid)
{
//仿函数
struct Min
{
bool operator()( Node* t1, Node* t2)
{
return (t1->_weight)< (t2->_weight);
}
};
//建小堆
Heap<Node*, Min> min_heap;
for (size_t i = 0; i < size; i++)
{
if (a[i] != invalid)
{
Node* newNode = new Node(a[i]);
min_heap.Push(newNode);
}
}
if (min_heap.Size() == 1)
{
_root = min_heap.Top();
}
while (min_heap.Size()>1)
{
Node* left = min_heap.Top();
min_heap.Pop();
Node* right = min_heap.Top();
min_heap.Pop();
Node* parent = new Node(left->_weight + right->_weight);
parent->_left = left;
parent->_right = right;
left->_parent = parent;
right->_parent = parent;
min_heap.Push(parent);
_root = parent;
}
}
Node* GetRoot()
{
return _root;
}
~HuffmanTree()
{
assert(_root);
_HuffmanTreeDestory(_root);
_root = NULL;
}
protected:
void _HuffmanTreeDestory(Node* root)
{
if (root != NULL)
{
_HuffmanTreeDestory(root->_left);
_HuffmanTreeDestory(root->_right);
delete root;
root = NULL;
}
}
Node* _root;
}; 3.接下来我要开始给大家解析一下文件压缩是怎么回事。
文件压缩就是想要让文件变得小一点,节省存储空间,用哈夫曼树实现文件压缩的原理就是让其所占得内存变小,但怎样让它的存储空间变小呢?举例说明,比如存一个文件aaaabbbccd
1>首先统计每个字符出现的个数,然后用这些字符出现的个数来构造哈夫曼树,构造出来的哈夫曼树我们可以看到,每个叶子节点都是字符出现的次数,看图更好的说明一下:
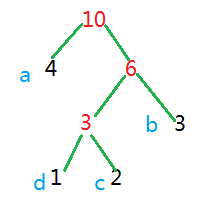
2>一个字符占一个字节的存储空间,要想办法来减少它所占用的内存,我们可以用哈夫曼编码来实现,就是说从根结点开始,向左走我们规定为0,向右走规定为1,每条路径都是不是1就是0,直到走到根节点,形成字符对应的哈夫曼编码,如图:

3>实现对文件的压缩设置,我们将每个字符都生成哈夫曼编码之后,每一个码都只是占用内存的1位,我们将每8位为一组,写入到压缩文件中,最后不够8位的要进行移位操作,这样才能保证所有的编码是连续的。
例子中的编码为:

最后编码生了6位,需要左移2位才能保证解压缩的时候不会出现问题。
4>需要生成配置文件,来保存每个字符,以及每个字符出现的次数
5>要知道文件中的字符最多只有256种,所以我们可以定义一个数组来存储这些字符,同样这个数组不能使普通数组,应该是一个结构体数组,每个数组元素应该包含字符,字符出现的个数,以及字符对应的编码,定义如下:
//字符信息
typedef long long LongType;
struct CharInfo
{
unsigned char _ch;//字符
LongType _count;//字符在文件中出现的个数
string _code;//哈夫曼编码
CharInfo(LongType count=0)
:_ch(0)
,_count(count)
{}
CharInfo operator + (const CharInfo& info)
{
return CharInfo(_count + info._count);
}
bool operator < (const CharInfo& info)
{
return _count < info._count;
}
bool operator >(const CharInfo& info)
{
return _count>info._count;
}
bool operator !=(const CharInfo& info)
{
return _count != info._count;
}
bool operator ==(const CharInfo& info)
{
return _count == info._count;
}
};6>实现解压缩就是压缩的逆过程,从配置文件中获取字符出现的次数,重建哈夫曼树,从压缩文件的第一个字符开始,比较其二进制的每一位,是0的话,从根结点开始,向左走一步,是1的话,从根结点向右走一步,比较8次还没有找到叶子节点,就接着从压缩文件中获取字符,直到找到叶子节点为止,将叶子节点的字符信息写到解压缩文件中
接下来就是完整的代码了
class FileCompress
{
typedef HuffmanTreeNode Node;
public:
FileCompress()
{
for (int i = 0; i < 256; i++)
{
_Info[i]._ch = i;
}
}
string Compress(const char* filename)
{
//1.统计字符出现的次数
assert(filename);
//二进制方式读
FILE* fout = fopen(filename,"rb");
assert(fout);
//读取文件中的字符
int ch = fgetc(fout);
while (ch != EOF)
{
_Info[ch]._count++;
ch = fgetc(fout);
}
//2.生成Huffman树
CharInfo invalid;
HuffmanTree Tree(_Info, 256,invalid);
//3.生成Huffman编码
string code;
MakeHuffmancode(Tree.GetRoot(),code);
Node* ROOT = Tree.GetRoot();
cout << "压缩" << ROOT->_weight._count<< "个字符" << endl;
//4.压缩
string CompressFilename = filename;
CompressFilename.append(".Compress");
FILE* fin = fopen(CompressFilename.c_str(), "wb");//二进制方式写入
fseek(fout,0,SEEK_SET);
ch = fgetc(fout);
unsigned char value = 0;
int pos = 0;
while (ch != EOF)
{
//code中只有0和1
code = _Info[ch]._code;
for (size_t i = 0; i < code.size(); i++)
{
if (code[i] == '1')
{
value <<= 1;
value |= 1;
}
else
{
value <<= 1;
value |= 0;
}
pos++;
if (pos == 8)
{
fputc(value,fin);
pos = 0;
value = 0;
}
}
ch = fgetc(fout);
}
if (pos != 8)
{
value <<= (8 - pos);
fputc(value, fin);
}
cout << "压缩文件的名字:" << filename << endl;
fclose(fout);
fclose(fin);
//5.创建配置文件,其中存放的树字符以及字符出现的个数
string ConfigFilename = filename;
ConfigFilename.append(".config");
FILE* finConfig = fopen(ConfigFilename.c_str(), "wb");
string Line;
char Buff[128];
for (int i = 0; i < 256; i++)
{
if (_Info[i]._count != 0)
{
fputc(_Info[i]._ch, finConfig);
Line += ',';
_itoa((int)_Info[i]._count, Buff, 10);
Line += Buff;
Line += '\n';
fputs(Line.c_str(), finConfig);
Line.clear();
}
}
fclose(finConfig);
return CompressFilename;
}
//6.解压缩
string UnCompress(const char* filename)
{
assert(filename);
//打开配置文件
string name = filename;
size_t _index = name.rfind('.');
string Configfilename = name.substr(0, _index);
Configfilename += ".config";
FILE* foConfigname = fopen(Configfilename.c_str(), "rb");
cout << "解压缩文件的名字:" << name << endl;
//重建_Info的哈希表
string Line;
while (ReadLine(foConfigname, Line))
{
unsigned char ch = Line[0];
_Info[ch]._ch = Line[0];
LongType count = atoi(Line.substr(2).c_str());
_Info[ch]._count = count;
Line.clear();
}
//解压缩文件名
string Compressfilename = filename;
size_t index = Compressfilename.rfind('.');
string UnCompressFilename = Compressfilename.substr(0,index);
UnCompressFilename.append(".UnCompress");
//生成Huffman树
CharInfo invalid;
HuffmanTree Tree(_Info, 256, invalid);
//打开要被解压缩的文件
FILE* fout = fopen(filename,"rb");
//创建解压缩文件并写入
FILE* fin = fopen(UnCompressFilename.c_str(),"wb");
Node* root = Tree.GetRoot();
Node* cur = root;
LongType count = root->_weight._count;
cout << "解压缩" << count << "个字符" << endl;
//文件中只有一种字符时,没有哈夫曼编码,要特殊处理
/*if (cur->_left == NULL&&cur->_right == NULL)
{
while (count--)
{
fputc(root->_weight._ch,fin);
}
return UnCompressFilename;
}*/
//文件中只有一种字符的情况
unsigned Readch = fgetc(fout);
if (Readch == 0)
{
while (count--)
{
fputc(root->_weight._ch, fin);
}
return UnCompressFilename;
}
int pos = 7;
while (Readch != EOF)
{
if (pos >= 0)
{
if (((Readch >> pos) & 1) == 1)
{
cur = cur->_right;
}
else
{
cur = cur->_left;
}
--pos;
if (cur->_left == NULL&&cur->_right == NULL)
{
fputc(cur->_weight._ch, fin);
cur = root;
//找到一个叶子节点,解压缩的字符个数减少一个
--count;
}
if (count == 0)
{
break;
}
}
else
{
pos = 7;
Readch = fgetc(fout);
}
}
return UnCompressFilename;
}
protected:
void MakeHuffmancode(Node* root, string code)
{
if (root == NULL)
return;
else if (root->_left == NULL&&root->_right == NULL)
{
_Info[(root->_weight)._ch]._code = code;
}
else
{
MakeHuffmancode(root->_left, code + '0');//向左走编码加0
MakeHuffmancode(root->_right, code + '1');//向右走编码加1
}
}
//读取一行字符
bool ReadLine(FILE* filename, string& Line)
{
int ch = 0;
while ((ch=fgetc(filename))!= EOF)
{
if (ch == '\n'&&Line.size() != 0)
{
return true;
}
Line += ch;
}
return false;
}
protected:
CharInfo _Info[256];
};
void Test()
{
//压缩
FileCompress f1;
int begin = GetTickCount();
string Cf1 = f1.Compress("haha.txt");
//string Cf1 = f1.Compress("photo.jpg");
//string Cf1 = f1.Compress("Music.m4a");
int end = GetTickCount();
cout << "压缩时间为:" << end - begin << endl;
//解压缩
FileCompress f2;
int begin1 = GetTickCount();
string UnCf1 = f2.UnCompress("haha.txt.Compress");
//string UnCf1 = f2.UnCompress("photo.jpg.Compress");
//string UnCf1 = f2.UnCompress("Music.m4a.Compress");
int end1 = GetTickCount();
cout << "解压缩时间为:" << end1 - begin1 << endl;
} 结果为:
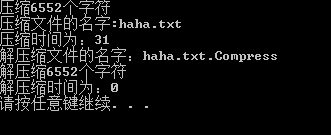
在文件中生成了对应的压缩文件,配置文件,以及解压缩文件,

解压缩文件与源文件大小相同,压缩文件较源文件小,同样可以进行图片,视频,音频的测试,在这里我就不一一做测试了。
其中用到了许多关于文件的知识还有string的知识,substr()是字符串复制函数,可以指定复制字符的个数,c_str()返回指向字符串的指针,还用了其他一些函数,文件压缩综合了许多知识,要好好理解哈夫曼树以及文件压缩的实现思路,体改自己的融会贯通能力。