cs231n作业:assignment1 - two_layer_net
github地址:https://github.com/ZJUFangzh/cs231n
个人博客:fangzh.top
搭建一个两层的神经网络。
Forward pass
先计算前向传播过程,编辑cs231n/classifiers/neural_net.py的TwoLayerNet.loss函数
这个就和之前的svm和softmax一样了:
def loss(self, X, y=None, reg=0.0):
"""
Compute the loss and gradients for a two layer fully connected neural
network.
Inputs:
- X: Input data of shape (N, D). Each X[i] is a training sample.
- y: Vector of training labels. y[i] is the label for X[i], and each y[i] is
an integer in the range 0 <= y[i] < C. This parameter is optional; if it
is not passed then we only return scores, and if it is passed then we
instead return the loss and gradients.
- reg: Regularization strength.
Returns:
If y is None, return a matrix scores of shape (N, C) where scores[i, c] is
the score for class c on input X[i].
If y is not None, instead return a tuple of:
- loss: Loss (data loss and regularization loss) for this batch of training
samples.
- grads: Dictionary mapping parameter names to gradients of those parameters
with respect to the loss function; has the same keys as self.params.
"""
# Unpack variables from the params dictionary
W1, b1 = self.params['W1'], self.params['b1']
W2, b2 = self.params['W2'], self.params['b2']
N, D = X.shape
# Compute the forward pass
scores = None
#############################################################################
# TODO: Perform the forward pass, computing the class scores for the input. #
# Store the result in the scores variable, which should be an array of #
# shape (N, C). #
#############################################################################
Z1 = X.dot(W1) + b1
A1 = np.maximum(0, Z1)
scores = A1.dot(W2) + b2
#############################################################################
# END OF YOUR CODE #
#############################################################################
# If the targets are not given then jump out, we're done
if y is None:
return scores
# Compute the loss
loss = None
#############################################################################
# TODO: Finish the forward pass, and compute the loss. This should include #
# both the data loss and L2 regularization for W1 and W2. Store the result #
# in the variable loss, which should be a scalar. Use the Softmax #
# classifier loss. #
#############################################################################
scores -= np.max(scores, axis=1,keepdims=True)
exp_scores = np.exp(scores)
probs = exp_scores / np.sum(exp_scores,axis=1,keepdims=True)
y_label = np.zeros((N,probs.shape[1]))
y_label[np.arange(N),y] = 1
loss = (-1) * np.sum(np.multiply(np.log(probs),y_label)) / N
loss += reg * (np.sum(W1 * W1) + np.sum(W2 * W2))
#############################################################################
# END OF YOUR CODE #
#############################################################################
检验一下:
loss, _ = net.loss(X, y, reg=0.05)
correct_loss = 1.30378789133
# should be very small, we get < 1e-12
print('Difference between your loss and correct loss:')
print(np.sum(np.abs(loss - correct_loss)))
Difference between your loss and correct loss:
1.7985612998927536e-13
Backword pass
依旧是这个loss函数里面,根据W1,b1,W2,b2,求出grads,求导的公式课程里没给,不过NG老师给了,shallow neural networks,但是表示的维度不太一样,需要做稍微的修改:
# Backward pass: compute gradients
grads = {}
#############################################################################
# TODO: Compute the backward pass, computing the derivatives of the weights #
# and biases. Store the results in the grads dictionary. For example, #
# grads['W1'] should store the gradient on W1, and be a matrix of same size #
#############################################################################
dZ2 = probs-y_label
dW2 = A1.T.dot(dZ2)
dW2 /= N
dW2 += 2 * reg*W2
db2 = np.sum(dZ2,axis=0) / N
dZ1 = (dZ2).dot(W2.T) * (A1 > 0)
dW1 = X.T.dot(dZ1) / N + 2 * reg * W1
db1 = np.sum(dZ1,axis=0) / N
grads['W2'] = dW2
grads['b2'] = db2
grads['W1'] = dW1
grads['b1'] = db1
#############################################################################
# END OF YOUR CODE #
#############################################################################
检验一下:
W2 max relative error: 3.440708e-09
b2 max relative error: 3.865091e-11
W1 max relative error: 3.561318e-09
b1 max relative error: 1.555471e-09
train network
补全train()函数,其实是一样的,先创建一个minibatch,然后计算得到loss和grads,更新params:
#########################################################################
# TODO: Create a random minibatch of training data and labels, storing #
# them in X_batch and y_batch respectively. #
#########################################################################
batch_inx = np.random.choice(num_train,batch_size)
X_batch = X[batch_inx,:]
y_batch = y[batch_inx]
#########################################################################
# END OF YOUR CODE #
#########################################################################
# Compute loss and gradients using the current minibatch
loss, grads = self.loss(X_batch, y=y_batch, reg=reg)
loss_history.append(loss)
#########################################################################
# TODO: Use the gradients in the grads dictionary to update the #
# parameters of the network (stored in the dictionary self.params) #
# using stochastic gradient descent. You'll need to use the gradients #
# stored in the grads dictionary defined above. #
#########################################################################
self.params['W1'] -= learning_rate * grads['W1']
self.params['b1'] -= learning_rate * grads['b1']
self.params['W2'] -= learning_rate * grads['W2']
self.params['b2'] -= learning_rate * grads['b2']
#########################################################################
# END OF YOUR CODE #
#########################################################################
再补全predict()函数
###########################################################################
# TODO: Implement this function; it should be VERY simple! #
###########################################################################
score = self.loss(X)
y_pred = np.argmax(score,axis=1)
###########################################################################
# END OF YOUR CODE #
###########################################################################
然后可以计算画图了:
net = init_toy_model()
stats = net.train(X, y, X, y,
learning_rate=1e-1, reg=5e-6,
num_iters=100, verbose=False)
print('Final training loss: ', stats['loss_history'][-1])
# plot the loss history
plt.plot(stats['loss_history'])
plt.xlabel('iteration')
plt.ylabel('training loss')
plt.title('Training Loss history')
plt.show()
载入数据集
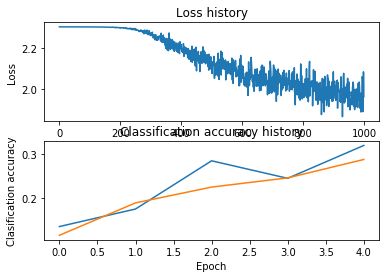
接下来就可以载入大的数据集,进行训练了,代码都写好了,
得到的准确度是:0.287
画个图:
调超参数
best_net = None # store the best model into this
results = {}
best_val = -1
learning_rates = [1.2e-3, 1.5e-3, 1.75e-3]
regularization_strengths = [1, 1.25, 1.5 , 2]
#################################################################################
# TODO: Tune hyperparameters using the validation set. Store your best trained #
# model in best_net. #
# #
# To help debug your network, it may help to use visualizations similar to the #
# ones we used above; these visualizations will have significant qualitative #
# differences from the ones we saw above for the poorly tuned network. #
# #
# Tweaking hyperparameters by hand can be fun, but you might find it useful to #
# write code to sweep through possible combinations of hyperparameters #
# automatically like we did on the previous exercises. #
#################################################################################
for lr in learning_rates:
for reg in regularization_strengths:
net = TwoLayerNet(input_size, hidden_size, num_classes)
loss_hist = net.train(X_train, y_train, X_val, y_val,
num_iters=1000, batch_size=200,
learning_rate=lr, learning_rate_decay=0.95,
reg=reg, verbose=False)
y_train_pred = net.predict(X_train)
y_val_pred = net.predict(X_val)
y_train_acc = np.mean(y_train_pred==y_train)
y_val_acc = np.mean(y_val_pred==y_val)
results[(lr,reg)] = [y_train_acc, y_val_acc]
if y_val_acc > best_val:
best_val = y_val_acc
best_net = net
for lr, reg in sorted(results):
train_accuracy, val_accuracy = results[(lr, reg)]
print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
lr, reg, train_accuracy, val_accuracy))
print('best validation accuracy achieved during cross-validation: %f' % best_val)
#################################################################################
# END OF YOUR CODE #
#################################################################################