算法-时间复杂度和空间复杂度
2.9 算法时间复杂度
2.9.1 算法时间复杂度定义
在进行算法分析时 , 语句总的执行次数 T ( n )是关子问题规模n的函数,进而分析 T ( n )随 n 的变化情况并确定T(n)的数量级。 算法的时间复杂度,也就是算法的时间量度,记作: T(n)=O(f(n))。 它表示随问题规模 n 的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称为时间复杂度。其中f(n) 是问题规模 n 的某个函数。
这样用大写 O()来体现算法时间复杂度的记法,我们称之为大 O 记法。
一般情况下,随着 n 的增大, T(n)增长最慢的算法为最优算法。
显然,由此算法时间复杂度的定义可知,我们的三个求和算法的时间复杂度分别为 O(n) , O(1) , O(n^2)。我们分别给它们取了非官方的名称, O(1) 叫常数阶、 O(n)叫线性阶、 O(n^2) 叫平方阶,当然,还有其他的一些阶,我们之后会介绍。
2.9.2 推导大 O 阶方法
那么如何分析一个算法的时间复杂度呢?即如何推导大 O 阶呢?我们给出了下面的推导方法,基本上,这也就是总结前面我们举的例子。
推导大 O 阶 :
1.用常数 1 取代运行时间中的所有加法常数 。
2.在修改后的运行次数函数中,只保留最高阶项 。
3.如果最高阶项存在且不是 1 ,则去除与这个项相乘的常数。
得到的结果就是大 O 阶。
哈,仿佛是得到了游戏攻略一样,我们好像已经得到了一个推导算法时间复杂度的万能公式。可事实上,分析一个算法的时间复杂度,没有这么简单,我们还需要多看几个例子。
2.9.3 常数阶
首先顺序结构的时间复杂度。下面这个算法,也就是刚才的第二种算法(高斯算法) .为什么时间复杂度不是 O(3) .而是 O(1) 。
int 1, sum = 0,n = 100; /* 执行1次 */
sum = (1 + n) * n /2; /* 执行1次 */
System.out.println(sum); /* 执行1次 */
这个算法的运行次数函数是 f (n) =3。 根据我们推导大 O 阶的方法,第一步就是把常数项 3 改为 1。在保留最高阶项时发现,它根本没有最高阶项,所以这个算法的时间复杂度为 0(1)。
另外,我们试想一下,如果这个算法当中的语句 sum= ( 1+n ) *n/2 有 10 句,即:
int 1, sum = 0,n = 100; /* 执行1次 */
sum = (1 + n) * n /2; /* 执行1次 */
sum = (1 + n) * n /2; /* 执行2次 */
sum = (1 + n) * n /2; /* 执行3次 */
sum = (1 + n) * n /2; /* 执行4次 */
sum = (1 + n) * n /2; /* 执行5次 */
sum = (1 + n) * n /2; /* 执行6次 */
sum = (1 + n) * n /2; /* 执行7次 */
sum = (1 + n) * n /2; /* 执行8次 */
sum = (1 + n) * n /2; /* 执行9次 */
sum = (1 + n) * n /2; /* 执行10次 */
System.out.println(sum); /* 执行1次 */
事实上无论 n 为多少,上面的两段代码就是 3 次和 12 次执行的差异。这种与问题的大小无关 (n的多少) ,执行时间恒定的算法,我们称之为具有 O(1)的时间复杂度,又叫常数阶。
注意 : 不管这个常数是多少,我们都记作 O(1) ,而不能是 O(3) 、 O(12)等其他任何数字,这是初学者常常犯的错误。
对于分支结构而言,无论是真,还是假,执行的次数都是恒定的,不会随着n的变大而发生变化,所以单纯的分支结构(不包含在循环结构中),其时间复杂度也是O(1)。
2.9.4 线性阶
线性阶的循环结构会复杂很多。要确定某个算法的阶次,我们常常需要确定某个特定语句或某个语句集运行的次数。因此,我们要分析算法的复杂度,关键就是要分析循环结构的运行情况。
下面这段代码,它的循环的时间复杂度为 O(n) , 因为循环体中的代码须要执行n次。
int i;
for (i = 0; i < n; i++){
/ *时间复杂度为O(1)的程序步骤序列 * /
}2.9.5 对数阶
下面的这段代码,时间复杂度又是多少呢?
int count = 1;
while (count < n){
count = count * 2;
/* 时间复杂度为 O(1)的程序步骤序列 */
}
由于每次 count 乘以 2 之后,就距离 n 更近了一分。 也就是说,有多少个 2 相乘后大于 n ,则会退出循环。由 2^x=n 得到x=log2(n) 。 所以这个循环的时间复杂度为O(log(n)) 。
2.9.6 平方阶
下面例子是一个循环嵌套,它的内循环刚才我们已经分析过,时间复杂度为O(n) 。
int i , j ;
for (i = 0; i < n; i++){
for ( j = 0 ; j < n ; j++ ){
/* 时间复杂度为 O(1)的程序步骤序列 */
}
}
而对于外层的循环,不过是内部这个时间复杂度为 O(n)的语句,再循环 n 次 。 所以这段代码的时间复杂度为 O(n^2)。
如果外循环的循环次数改为了m, 时间复杂度就变为 O(m×n)。
int i , j ;
for (i = 0; i < m; i++){
for ( j = 0 ; j < n ; j++ ){
/* 时间复杂度为 O(1)的程序步骤序列 */
}
}
所以我们可以总结得出,循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。
那么下面这个循环嵌套,它的时间复杂度是多少呢?
int i,j, n = 100;
for(i = 0; i < n; i++){
for(j = i; j < n; j++){/*注意 j = i 而不是0*/
/*时间复杂度为 O(1)的程序步骤序列*/
}
}
由于当 i= 0时,内循环执行了n次,当 i =1时,执行了n-1次,……当i=n一1时,执行了1次。所以总的执行次数为:
n+(n-1)+(n-2)+…+ 1=n(n+1)/2=n^2/2+n/2
用我们推导大 O 阶的方法,第一条,没有加法常数不予考虑; 第二条,只保留最高阶项,因此保留n^2/2; 第三条,去除这个项相乘的常数,也就是去除 1/2 ,最终这段代码的时间复杂度为 O(n^2) 。
从这个例子,我们也可以得到一个经验,其实理解大O 推导不算难,难的是对数列的一些相关运算,这更多的是考察你的数学知识和能力,所以想考研的朋友,要想在求算法时间复杂度这里不失分,可能需要强化你的数学,特别是数列方面的知识和解题能力 。
我们继续看例子,对于方法调用的时间复杂度又如何分析。
int i,n=100;
for(i = 0; i < n; i++){
function(i);
}
//上面这段代码调用一个函数 function。
static void function(int count){
System.out.println(count);
}
函数体是打印这个参数。 其实这很好理解, function 函数的时间复杂度是 O(1) 。所以整体的时间复杂度为 O(n) .
假如 function 是下面这样的:
static void function(int count){
int j,n=100;
for(j = count; j < n; j++){
/*时间复杂度为 O(1)的程序步骤序列*/
}
}
事实上 ,这和刚才举的例子是一样的,只不过把嵌套内循环放到了函数中,所以最终的时间复杂度为 0(n^2) 。
下面这段相对复杂的语句 :
n++; / * 执行1次 */
function(n); / * 执行n次 */
int i,j; / * 执行1次 */
for(i = 0; i < n; i++){ / * 执行n(n+1)/2次 */
for(j = i; j < n; i++){
/*时间复杂度为 O(1)的程序步骤序列*/ / * 执行1次 */
}
}
for(i = 0; i < n; i++){ / * 执行n^2次 */
function(i);
}
它的执行次数 f(n)=1+n+n^2+n(n+1)/2 =(3/2)n^2+(3/2)n +1 ,根据推导大 O 阶的方法,最终这段代码的时间复杂度也是 O(n^2) 。
2.10 常见的时间复杂度
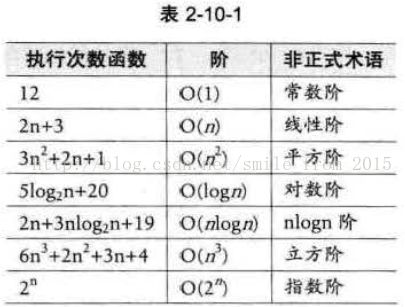
常见的时问复杂度如表 2-10-1 所示。
常用的时间复杂度所耗费的时间从小到大依次是 :
我们前面已经谈到了O(1)常数阶、O(nlogn)对数阶、O(n)线性阶、O(n^2)平方阶等,至于O(nlogn)我们将会在今后的课程中介绍,而像 O(n^3),过大的 n 都会使得结果变得不现实。同样指数阶 0(2^n)和阶乘阶O(n!)等除非是很小的n值,否则哪怕n只是100,都是噩梦般的运行时间。所以这种不切实际的算法时间复杂度,一般我们都不去讨论它。
2.11 最坏情况与平均情况
你早晨上班出门后突然想起来,手机忘记带了,这年头,钥匙、钱包(现在支付宝、微信)、 手机三大件,出门哪样也不能少呀。于是回家找。打开门一看,手机就在门口的台子上,原来是出门穿鞋时忘记拿了。这当然是比较好,基本没花什么时间寻找。可如果不是放在那里,你就得进去到处找,找完客厅找卧室 、找完卧室找厨房 、找完厨房找卫生间,就是找不到,时间一分一秒的过去,你突然想起来,可以用家里座机打一下手机,听着手机铃声来找呀,真是笨。终于找到了,在床上枕头下面。你再去上班,迟
到。见鬼,这一年的全勤奖,就因为找手机给黄了。
找东西有运气好的时候,也有怎么也找不到的情况。但在现实中,通常我们碰到的绝大多数既不是最好的也不是最坏的,所以算下来是平均情况居多。
算法的分析也是类似 ,我们查找一个有 n 个随机数字数组中的某个数字, 最好的情况是第一个数字就是,那么算法的时间复杂度为 O(1) ,但也有可能这个数字就在最后一个位置上待着,那么算法的时间复杂度就是 O(n),这是最坏的一种情况了。
最坏情况运行时间是一种保证,那就是运行时间将不会再差了。在应用中,这是一种最重要的需求,通常,除非特别指定,我们提到的运行时间都是最坏情况的运行时间 。
而平均运行时间也就是从概率的角度看 ,这个数字在每一个位置的可能性是相同的,所以平均的查找时间为 n/2 次后发现这个目标元素。
平均运行时间是所有情况中最有意义的,因为它是期望的运行时间。也就是说,我们运行一段程序代码时,是希望看到平均运行时间的。可现实中 ,平均运行时间很难通过分析得到,一般都是通过运行一定数量的实验数据后估算出来的。
对算法的分析,一种方法是计算所有情况的平均值,这种时间复杂度的计算方法称为平均时间复杂度 。另一种方法是计算最坏情况下的时间复杂度,这种方法称为最坏时间复杂度。一般在没有特殊说明的情况下,都是指最坏时间复杂度。
2.12 算法空间复杂度
我们在写代码时,完全可以用空间来换取时间, 比如说,要判断某某年是不是闰年,你可能会花一点心思写了一个算法,而且由于是一个算法,也就意味着,每次给一个年份,都是要通过计算得到是否是闰年的结果。 还有另一个办法就是,事先建立一个有2050个元素的数组(年数略比现实多一点) ,然后把所有的年份按下标的数字对应,如果是闰年,此数组项的值就是 1 ,如果不是值为 0。这样,所谓的判断某一年是否是闰年,就变成了查找这个数组的某一项的值是多少的问题。 此时,我们的运算是最小化了,但是硬盘上或者内存中需要存储这 2050 个 0 和 1 。
这是通过一笔空间上的开销来换取计算时间的小技巧。到底哪一个好,其实要看你用在什么地方。
算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算公式记作: S(n)= O(f(n)),其中,n为问题的规模, f(n)为语句关于 n 所占存储空间的函数。
一般情况下, 一个程序在机器上执行时,除了需要存储程序本身的指令、常数、变量和输入数据外,还需要存储对数据操作的存储单元,若输入数据所占空间只取决于问题本身,和算法无关,这样只需要分析该算法在实现时所需的辅助单元即可。若算法执行时所需的辅助空间相对于输入数据量而言是个常数,则称此算法为原地工作,空间复杂度为 O(1) 。
通常,我们都使用"时间复杂度"来指运行时间的需求,使用"空间复杂度"指空间需求。当不用限定词地使用"复杂度'时,通常都是指时间复杂度。显然我们这本书重点要讲的还是算法的时间复杂度的问题。
2.13 总结回顾
不容易,终于又到了总结的时间。
我们这一章主要谈了算法的一些基本概念。谈到了数据结构与算法的关系是相互依赖不可分割的 。
算法的定义:算法是解决特定问题求解步骤的描述,在计算机中为指令的有限序列,并且每条指令表示一个或多个操作。
算法的特性 : 有穷性、确定性、可行性、输入、输出 。
算法的设计的要求 : 正确性、可读性、健壮性、高效率和低存储量需求。
算法特性与算法设计容易混,需要对比记忆。
算法的度量方法 : 事后统计方法(不科学、不准确) 、事前分析估算方法。
在讲解如何用事前分析估算方法之前,我们先给出了函数渐近增长的定义。
函数的渐近增长:给定两个函数 f(n)和 g(n),如果存在一个整数 N使得对于所有的 n > N, f(n)总是比 g(n)大,那么,我们说 f(n)的增长渐近快于 g(n) 。 于是我们可以得出一个结论,判断一个算法好不好,我们只通过少量的数据是不能做出准确判断的,如果我们可以对比算法的关键执行次数函数的渐近增长性,基本就可以分析出 :某个算法,随着 n 的变大,它会越来越优于另一算法,或者越来越差于另一算法。
然后给出了算法时间复杂度的定义和推导大 O 阶的步骤。
推导大O阶:
• 用常数 1 取代运行时间中的所有加法常数。
• 在修改后的运行次数函数中,只保留最高阶项。
• 如果最高阶项存在且不是 1 ,则去除与这个项相乘的常数。
得到的结果就是大 O 阶。
通过这个步骤,我们可以在得到算法的运行次数表达式后,很快得到它的时间复杂度,即大O阶。同时我也提醒了大家,其实推导大O阶很容易,但如何得到运行次数的表达式却是需要数学功底的。
接着我们给出了常见的时间复杂度所耗时间的大小排列:
最后,我们给出了关于算法最坏情况和平均情况的概念,以及空间复杂度的概念。
2.14 结尾语
很多学生,学了四年计算机专业,很多程序员,做了很长时间的编程工作,却始终都弄不明白算法的时间复杂度的估算,这是很可悲的一件事。因为弄不清楚,所以也就从不深究自己写的代码是否效率低下,是不是可以通过优化让计算机更加快速高效。
他们通常的借口是,现在CPU越来越快,根本不用考虑算法的优劣,实现功能即可,用户感觉不到算法好坏造成的快慢。可事实真是这样吗?还是让我们用数据来说话吧。
假设 CPU 在短短几年间,速度提高了 100 倍,这其实已经很夸张了 。而我们的某个算法本可以写出时间复杂度是 O(n)的程序,却写出了O(n²)的程序,仅仅因为容易想到,也容易写。即在 O(n²) 的时间复杂度算法程序下,速度其实只提高了10倍(√100 =10 ) ,而对于O(n)时间复杂度的算法来说,那才是真的 100倍。
也就是说,一台老式 CPU 的计算机运行O(n)的程序和一台速度提高 100 倍新式CPU 运行0(n²)的程序。最终效率高的胜利方却是老式 CPU的计算机,原因就在于算法的优劣直接决定了程序运行的效率。
也许你就可以深刻的感受到,愚公移山固然可敬,但发明炸药和推土机,可能更加实在和聪明(如图 2-14-1 所示)。
希望大家在今后的学习中,好好利用算法分析的工具 ,改进自己的代码 ,让计算机轻松一点,这样你就更加胜人一筹。
引用《大话数据结构》作者:程杰