求两个正整数的最小公倍数
Java语言程序设计(基础篇)
编程综合题 6.29
求最小公倍数
编写程序,提示用户输入两个整数并求它们的最小公倍数(LCM)。
两个数的最小公倍数是指这两书的倍数中最小的数。
例如,
8和12的最小公倍数是24,
15和25的最小公倍数是75,
120和150的最小公倍数是600。
求最小公倍数的方法很多,在本练习中采用以下方法:
为求两个正整数的最小公倍数,首先为每个数创建一个素数因子表,的第一列包含所有素数因子,第二列为该数中对应素数因子出现的次数。
例如,120的素数因子为2,2,2,3,5,所以120的素数因子表如下所示:
120的素数因子 出现次数
2 3
3 1
5 1
150的素数因子 出现次数
2 1
3 1
5 2
两个数的最小公倍数由这两个数种出现频率最高的因子构成,所以,120和150的最小公倍数为2*2*2*3*5*5=600。其中2在120中出现了3次,3在120中出现了1次,5在150中出现了2次。
提示: 可以用二维数组表示素数因子表,编写 getPrimeFactors(int numer)方法,使其为素数因子表返回一个二维数组。
以下是我编程中的思路变化过程:
**LeastCommonMultiple1.java**
import javax.swing.JOptionPane;
public class LeastCommonMultiple1 {
static int MAX=10;
public static void main(String[] args) {
//get the integers from a dialog
String num1=JOptionPane.showInputDialog(null,"Input","Input Dialog",JOptionPane.QUESTION_MESSAGE);
//creat a array then initialize it ;
int[][] primeFactorList1=new int[2][MAX];
for(int j=0;j0].length;j++){
primeFactorList1[0][j]=1;
primeFactorList1[1][j]=0;
}
leastCommonMultiple(Integer.parseInt(num1),primeFactorList1);
//output the list to check ;
System.out.println(Integer.parseInt(num1)+" 's table of factors are");
for(int i=0;ifor(int j=0;j0].length;j++){
System.out.print(primeFactorList1[i][j]+" ");
}
System.out.println("");
}
String num2=JOptionPane.showInputDialog(null,"Input","Input Dialog",JOptionPane.QUESTION_MESSAGE);
//creat a array then initialize it ;
int[][] primeFactorList2=new int[2][MAX];
for(int j=0;j0].length;j++){
primeFactorList2[0][j]=1;
primeFactorList2[1][j]=0;
}
leastCommonMultiple(Integer.parseInt(num2),primeFactorList2);
System.out.println("\n"+Integer.parseInt(num2)+" 's table of factors are");
for(int i=0;ifor(int j=0;j0].length;j++){
System.out.print(primeFactorList2[i][j]+" ");
}
System.out.println("");
}
//calculate the least common multiple by the two list; that is a bug which need to fix!
int leastCommonMultiple=1;
for(int j=0;j0].length;j++){
if(primeFactorList1[0][j]==primeFactorList2[0][j]){
if(primeFactorList1[1][j]1][j])
leastCommonMultiple*=Math.pow((double)primeFactorList1[0][j], (double)primeFactorList2[1][j]);
else
leastCommonMultiple*=Math.pow((double)primeFactorList1[0][j], (double)primeFactorList1[1][j]);
}
else{
leastCommonMultiple*=Math.pow((double)primeFactorList1[0][j], (double)primeFactorList1[1][j]);
leastCommonMultiple*=Math.pow((double)primeFactorList2[0][j], (double)primeFactorList2[1][j]);
}
}
//output the LCM on both of console and dialog ;
String result=String.format("\n"+leastCommonMultiple+" is the least common multiple of "+Integer.parseInt(num1)+" and "+Integer.parseInt(num2));
System.out.println(result);
JOptionPane.showMessageDialog(null, result);
}
//it is able just to handle the integer whose number of factors is less than 10, and that's why i set a const argument "MAX" which is 10 default ;
public static void leastCommonMultiple(int number,int[][] primeFactorList){
int integer=number;
if(integer>=2){
for(int factor=2;factor<=integer;factor++){
if(integer%factor==0){
//load into the factor list;
updatePrimeFactorList(factor,primeFactorList);
integer=integer/factor;
//System.out.print(factor+" ");
leastCommonMultiple(integer,primeFactorList);
break;
}
//the following "else" is not essential,it may not miss somewhere
else
continue;
}
}
// else
// JOptionPane.showMessageDialog(null, "the number you put is not valid!","Error",JOptionPane.INFORMATION_MESSAGE);
}
//update the prime factors list ;
public static void updatePrimeFactorList(int num,int[][] primeFactorList){
for(int j=0;j0].length;j++){
if(primeFactorList[0][j]==num){
primeFactorList[1][j]++;
break;
}
else if(primeFactorList[0][j]==1){
primeFactorList[0][j]=num;
primeFactorList[1][j]=1;
break;
}
else
continue;
}
}
}
Result of test :

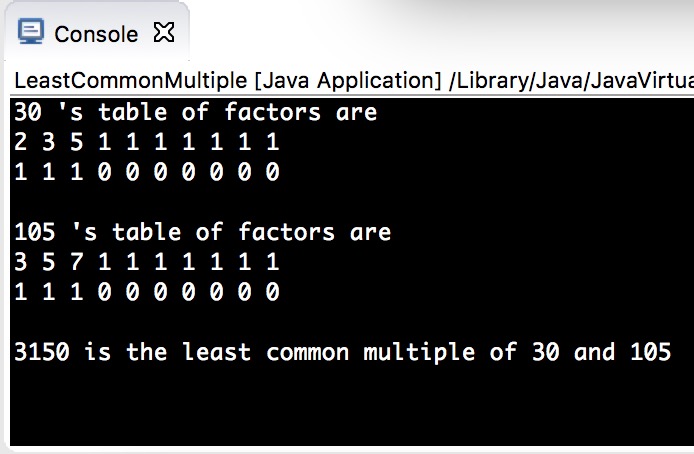
从输出这里你可以看到我采用的是二维数组primeFactorList:int[2][MAX]的形式存储整数的素数因子表,primeFactorList[i][0]存放素数因子,相应的 primeFactorList[i][1]存储相应素数因子出现的次数,并且开始用1初始化 primeFactorList[i][0],用0初始化 primeFactorList[i][1]。
**Bugs** - **很显然,如上图输出结果所示,在素数因子表里面存在着我们编程方式留下 痕迹,这对用户来说是不必要并且多余的。因此可以考虑只显示程序里的使用的“素数因子表”里有数学意义的内容,即去掉素数因子为1和出现次数为0的冗余数据。从这个角度思考,有了后来优化后的下面的程序。详情请见程序 LeastCommonMultiple2.java。**
**此外,leastCommonMultiple1.java程序中还存在一些(逻辑)错误(bug):** - **如下图所示,具体原因在于在通过两个数的苏素因子表计算 LCM(最小公倍数)时,是逐行逐行的对等比较,也就是说 primeFactorList1[i]和 primeFactorList2[i]比较,如果primeFactorList1[i][0]=primeFactorList2[i][0],则没有问题。这就要求两个整数的素因子数不仅个数相等,并且从小到大排列起来每一个都必须相同才能得出正确答案(如上面输出结果为120和150的输入):这显然是不对的。不仅个数不相等的不能处理,即使使那些有部分相同的素因子但是因为排列起来素因子不对应相等的两个数也是不能够处理的(如下面两张图所示)。** 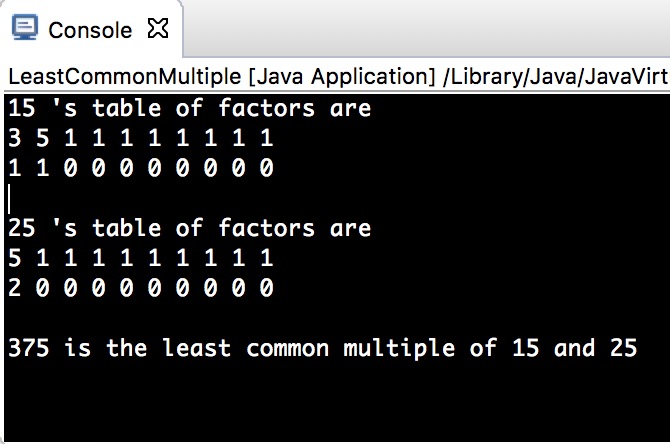
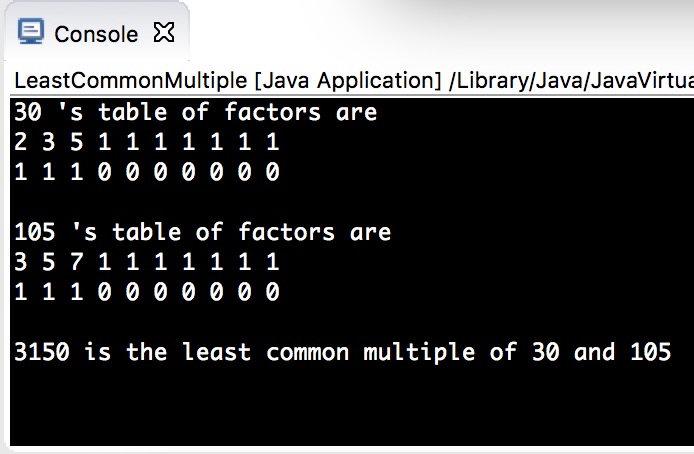
- …… ———-
LeastCommonMultiple2.java
package prime;
import javax.swing.JOptionPane;
import sortAlgorithms.*;
public class LeastCommonMultiple2 {
static int MAX=10;
//it is able just to handle the integer whose factor is less than 10;
public static void setPrimeFactorList(int number,int[][] pfl){
int integer=number;
if(integer>=2){
for(int factor=2;integer!=1&&factor2.0;factor++){
if(integer%factor==0){
//load into the factor list;
updatePrimeFactorList(factor,pfl);
integer=integer/factor;
factor=1;
}
}
}
}
//update the prime factors list ;
public static void updatePrimeFactorList(int num,int[][] primeFactorList){
for(int j=0;j0].length;j++){
if(primeFactorList[0][j]==num){
primeFactorList[1][j]++;
break;
}
else if(primeFactorList[0][j]==1){
primeFactorList[0][j]=num;
primeFactorList[1][j]=1;
break;
}
else
continue;
}
}
//calculate the least common multiple by the two list;
public static int calculateLCM(int[][] primeFactorList1,int[][] primeFactorList2,int[][] list){
int leastCommonMultiple=1;
int l=0;
//scan the former prime factor list;
for(int i=0;i0].length;i++){
list[0][l]=primeFactorList1[0][i];
list[1][l]=primeFactorList1[1][l];
int j=0;
for(;j0].length;j++){
if(primeFactorList1[0][i]==primeFactorList2[0][j]){
if(primeFactorList1[1][i]1][j])
list[1][l]=primeFactorList2[1][j];
break;
}
}
l++;
}
//scan the latter prime factor list;
for(int j=0;j0].length;j++){
int i=0;
for(;i0].length;i++){
if(primeFactorList2[0][j]==primeFactorList1[0][i])
break;
}
if(i==primeFactorList1[0].length){
list[0][l]=primeFactorList2[0][j];
list[1][l]=primeFactorList2[1][j];
l++;
}
}
for(int i=0;i0][i], list[1][i]);
}
return leastCommonMultiple;
}
public static void outputPrimeFactorList(int[][] l){
System.out.print("factor : ");
for(int j=0;j0].length;j++){
if(l[0][j]!=1)
System.out.print(l[0][j]+" ");
}
System.out.print("\npower : ");
for(int i=0;i0].length;i++){
if(l[1][i]!=0)
System.out.print(l[1][i]+" ");
}
System.out.println(" ");
}
public static void main(String[] args) {
int number1=1,number2=1;
int leastCommonMultiple=1;
int[][] primeFactorList1=new int[2][MAX];
int[][] primeFactorList2=new int[2][MAX];
int[][] list=new int[2][MAX*2];
//initializing
for(int i=0;i0].length;i++){
primeFactorList1[0][i]=1;
primeFactorList1[1][i]=0;
primeFactorList2[0][i]=1;
primeFactorList2[1][i]=0;
}
for(int i=0;i0].length;i++){
list[0][i]=1;
list[1][i]=0;
}
String num1=JOptionPane.showInputDialog(null,"Input","Input Dialog",JOptionPane.QUESTION_MESSAGE);
number1=Integer.parseInt(num1);
setPrimeFactorList(number1,primeFactorList1);
String num2=JOptionPane.showInputDialog(null,"Input","Input Dialog",JOptionPane.QUESTION_MESSAGE);
number2=Integer.parseInt(num2);
setPrimeFactorList(number2,primeFactorList2);
System.out.println(number1+" 's table of factors are");
outputPrimeFactorList(primeFactorList1);
System.out.println("\n"+number2+" 's table of factors are");
outputPrimeFactorList(primeFactorList2);
//output the LCM;
leastCommonMultiple=calculateLCM(primeFactorList1,primeFactorList2,list);
String result=String.format("\n"+leastCommonMultiple+" is the least common multiple of "+number1+" and "+number2);
System.out.println(result);
//invoke a sort function to make the LCM's table of factor more precise
/**there is a bug that the factor and their powers are not relevant,because the sort function cannot completely exchange two factor and its power in the form of list[2][MAX],it should be list[MAX][2] */
SortAlgorithmInIncreasingOrder.selectionSort(list[0]);
outputPrimeFactorList(list);
// JOptionPane.showMessageDialog(null, result);
}
}
**SortAlgorithmInIncreasingOrder.java**
package sortAlgorithms;
public class SortAlgorithmInIncreasingOrder {
public static void selectionSort(int[] array){
int temp=array[0];
for(int i=0;i<array.length-1;i++){
int k=i;
temp=array[i];
for(int j=i;j<array.length;j++){
if(temp>array[j]){
temp=array[j];
k=j;
}
}
array[k]=array[i];
array[i]=temp;
}
}
}
Result of test:
Optimization & Bugs:
LCM_LCM2对 LCM1的改进增加 calculateLCM()更加体现封装性,减少测试主函数的负担,同时增加了代码的可移植性
LCM_LCM2对 LCM1的改进_输出 LCM的素数因子表并且 提供正确的LCM 的素数因子表以供使用+LCM2的bug
3. LCM_LCM2_bug1_setPrimeFactorList 有问题——不能正确处理输入的素数——是因为LCM_LCM2对 LCM1的失误优化。
下图是 LeastCommonMultiple1.java 的输出结果。它确实是正确的。
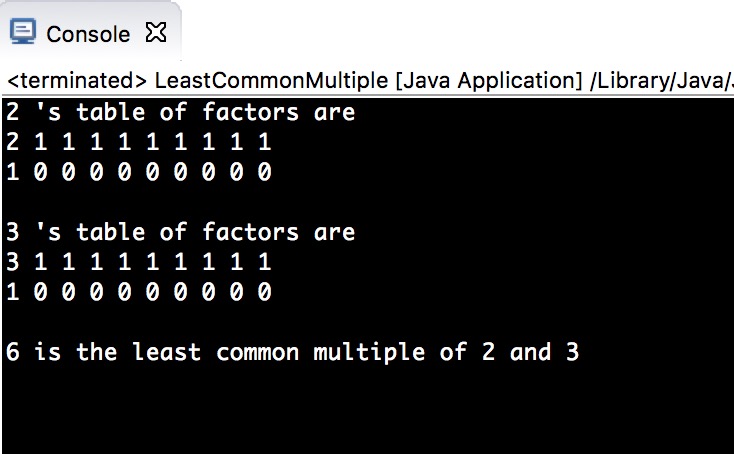
下面是 LeastCommonMultiple2.java 的输出结果——他显然不正确。
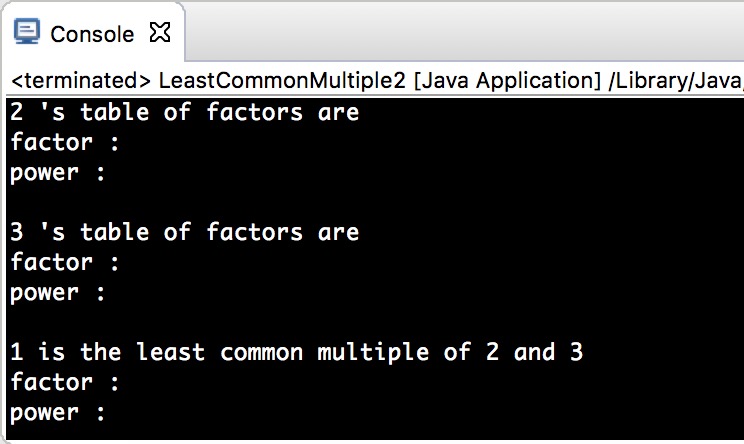
发生错误的地方在这里
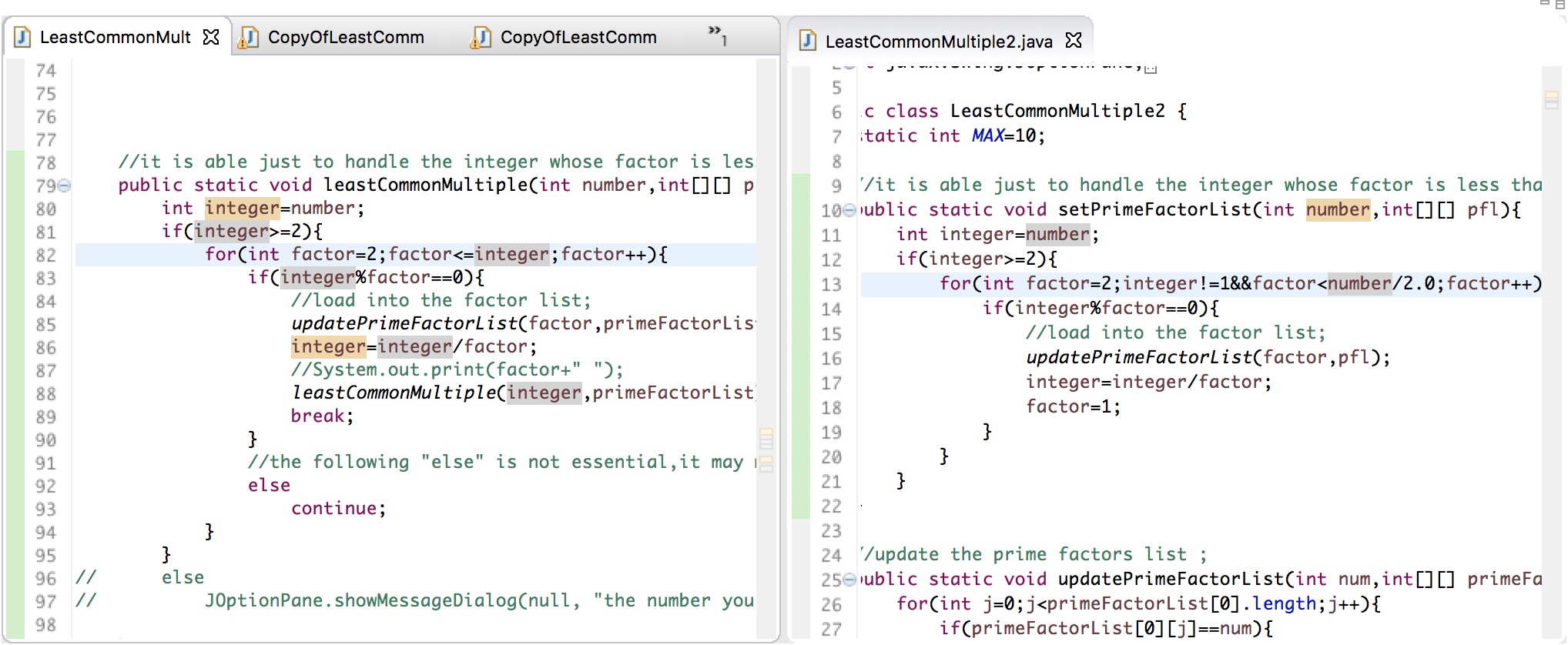
4. 同时,也不能输入1(1既不是素数也不是合数)——虽然输入的数据有硬性规定,但是对于用户来讲输入任何数据都是有可能的,算法的健壮性(软件测试)要求我们尽可能考虑一切可能的情况——从这个角度想,你还可以拓展到输入的数为负数的情形…… 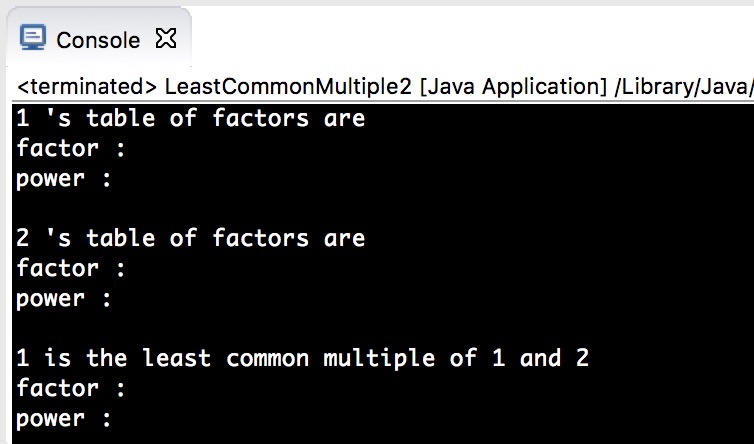
> 质数(素数)定义在大于1的自然数集合之上。 > 
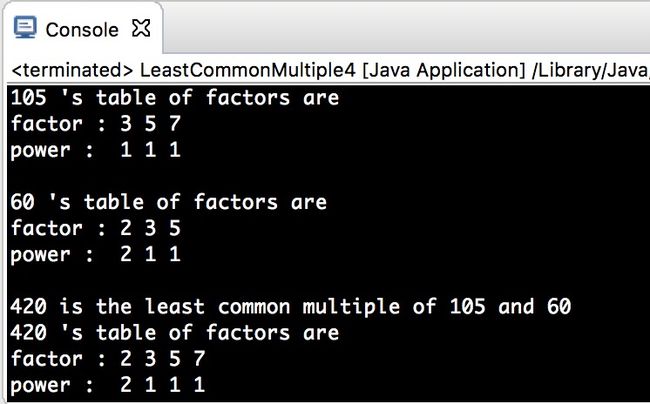
5. LCM_LCM2的bug3_对 LCM 的素数因子表的选择排序交换是不彻底的。在这里我们交换的是数组 list[0] 里的元素(质因子),相应的 list[1]里的元素(出现的次数/质因子的阶)并没有得到交换,如下图所示。显然,105和60的最小公倍数420的质因子表里的7的阶应该为2。而2的阶应该为1,正好是相反的。偶然里的必然就是算法的 bug。 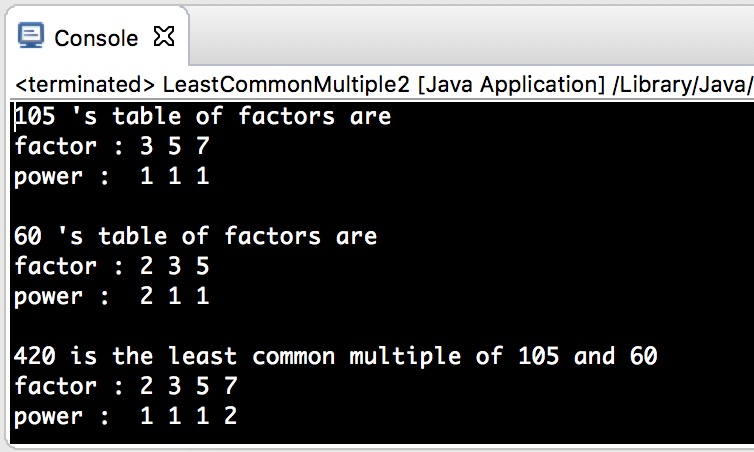 ———-
**LeastCommonMultiple4.java**
package prime;
import javax.swing.JOptionPane;
//import sortAlgorithms.SortAlgorithmInIncreasingOrder;
public class LeastCommonMultiple4 {
static int MAX=10;
//it is able just to handle the integer whose factor is less than 10;
public static void setPrimeFactorList(int number,int[][] pfl){
int integer=number;
if(integer>=2){
for(int factor=2;integer!=1&&factor<=integer;factor++){
if(integer%factor==0){
//load into the factor list;
updatePrimeFactorList(factor,pfl);
integer=integer/factor;
factor=1;
}
}
}
else if(integer==1){
pfl[0][1]++;
}
}
//update the prime factors list ;
public static void updatePrimeFactorList(int num,int[][] primeFactorList){
for(int j=0;jif(primeFactorList[j][0]==num){
primeFactorList[j][1]++;
break;
}
else if(primeFactorList[j][0]==1){
primeFactorList[j][0]=num;
primeFactorList[j][1]=1;
break;
}
else
continue;
}
}
//calculate the least common multiple by the two list;
public static int calculateLCM(int[][] primeFactorList1,int[][] primeFactorList2,int[][] list){
int leastCommonMultiple=1;
int l=0;
//scan the former prime factor list;
for(int i=0;i0]=primeFactorList1[i][0];
list[l][1]=primeFactorList1[l][1];
int j=0;
for(;jif(primeFactorList1[i][0]==primeFactorList2[j][0]){
if(primeFactorList1[i][1]1])
list[l][1]=primeFactorList2[j][1];
break;
}
}
l++;
}
//scan the latter prime factor list;
for(int j=0;jint i=0;
for(;iif(primeFactorList2[j][0]==primeFactorList1[i][0])
break;
}
if(i==primeFactorList1.length){
list[l][0]=primeFactorList2[j][0];
list[l][1]=primeFactorList2[j][1];
l++;
}
}
for(int i=0;i0], list[i][1]);
}
return leastCommonMultiple;
}
/*
public static void outputPrimeFactorList(int[][] l){
selectionSort(l);
System.out.print("factor : ");
for(int j=0;j
// there is another way to adjust——vertical display
public static void outputPrimeFactorList(int[][] l){
selectionSort(l);
System.out.println("factor power");
for(int j=0;jif (l[j][1]!=0)
System.out.println(" "+l[j][0]+" "+l[j][1]);
}
System.out.println(" ");
}
public static void selectionSort(int[][] array){
int[] tempArray;
for(int i=0;i1;i++){
int k=i;
tempArray=array[i];
for(int j=i;jif(tempArray[0]>array[j][0]){
tempArray=array[j];
k=j;
}
}
array[k]=array[i];
array[i]=tempArray;
}
}
public static void main(String[] args) {
int number1=1,number2=1;
int leastCommonMultiple=1;
int[][] primeFactorList1=new int[MAX][2];
int[][] primeFactorList2=new int[MAX][2];
int[][] list=new int[MAX*2][2];
//initializing
for(int i=0;i0]=1;
primeFactorList1[i][1]=0;
primeFactorList2[i][0]=1;
primeFactorList2[i][1]=0;
}
for(int i=0;i0]=1;
list[i][1]=0;
}
String num1=JOptionPane.showInputDialog(null,"Input","Input Dialog",JOptionPane.QUESTION_MESSAGE);
number1=Integer.parseInt(num1);
setPrimeFactorList(number1,primeFactorList1);
String num2=JOptionPane.showInputDialog(null,"Input","Input Dialog",JOptionPane.QUESTION_MESSAGE);
number2=Integer.parseInt(num2);
setPrimeFactorList(number2,primeFactorList2);
System.out.println(number1+" 's table of factors are");
outputPrimeFactorList(primeFactorList1);
System.out.println(number2+" 's table of factors are");
outputPrimeFactorList(primeFactorList2);
//output the LCM;
leastCommonMultiple=calculateLCM(primeFactorList1,primeFactorList2,list);
String result=String.format(leastCommonMultiple+" is the least common multiple of "+number1+" and "+number2);
System.out.println(result);
System.out.println(leastCommonMultiple+" 's table of factors are");
outputPrimeFactorList(list);
// JOptionPane.showMessageDialog(null, result);
}
}
Optimization & Bugs:
- LCM_LCM4对 LCM2的改进_将排序嵌在output函数里了——用 list[MAX][2]替换了 list[2][MAX]
- 修复不能输入素数的问题 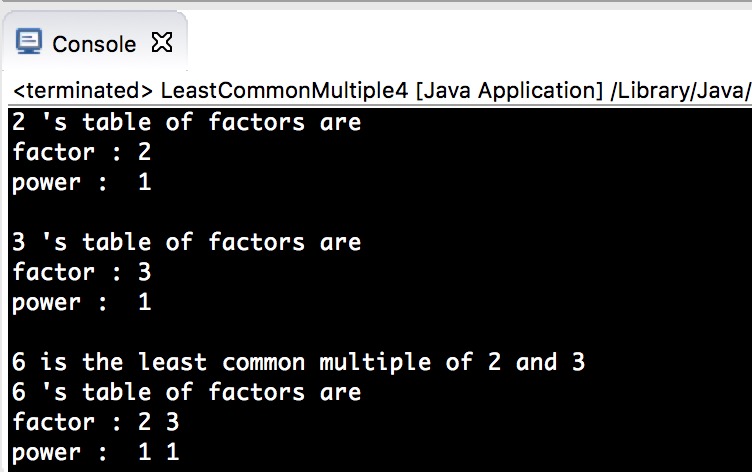
- 修复不能输入1的问题
LCM_LCM4里如果只用 list[Max][2]去替换 list[2][Max]而不修改 output 函数则会有显示错误,如下图:
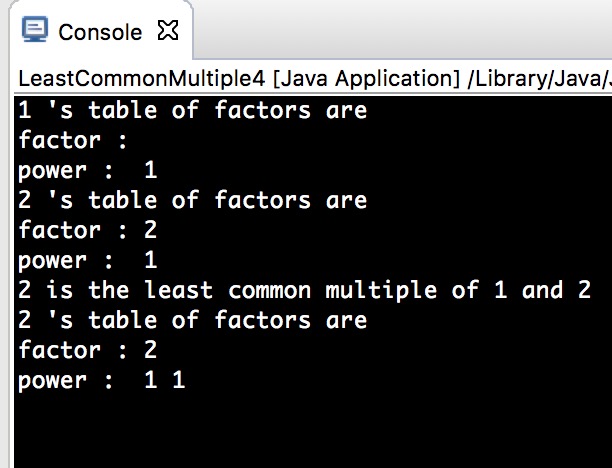
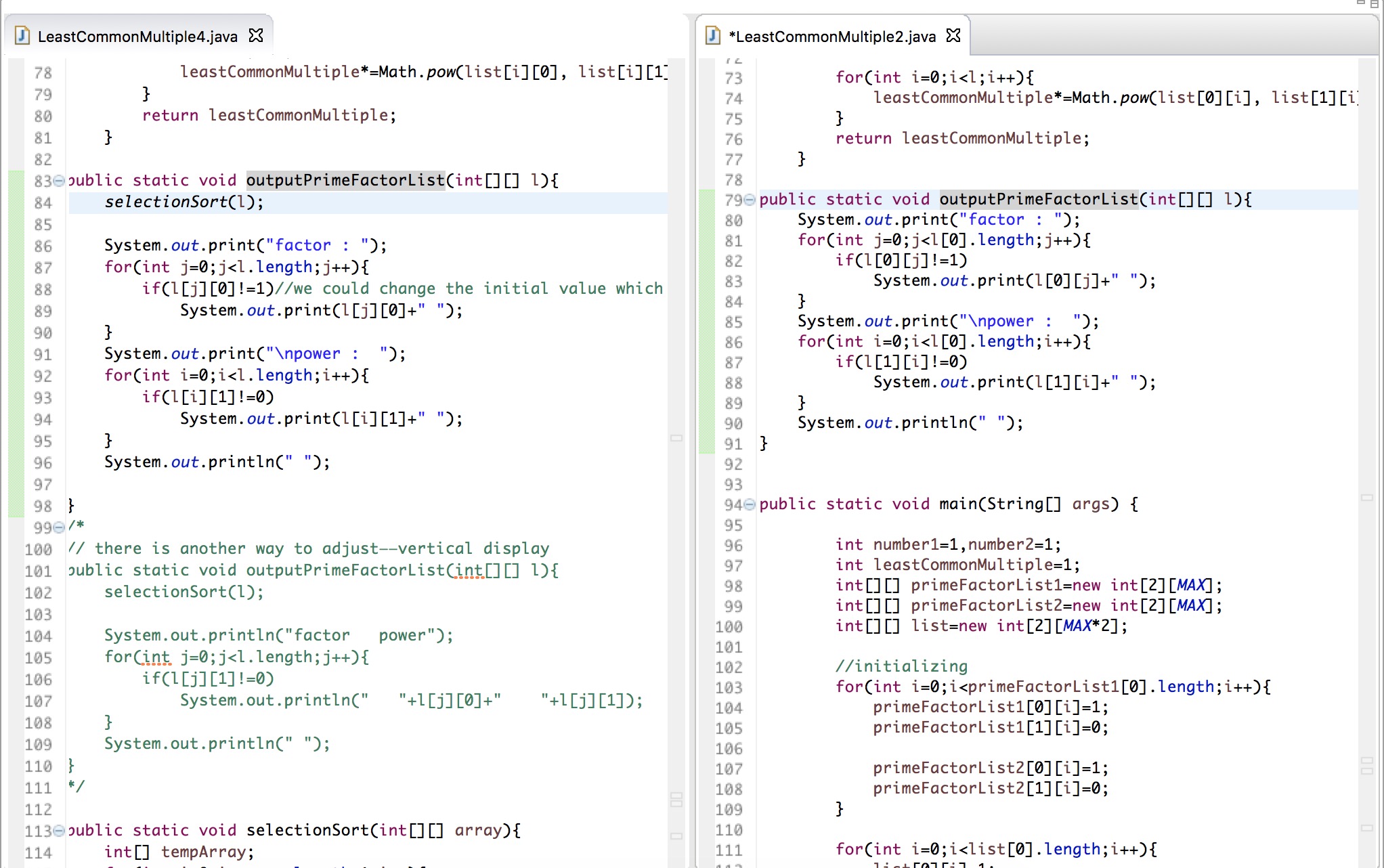
最后解决问题的办法是这样的——只需要将素因子表输出的方向换成垂直结果则没有问题。这也是最终代码形式。
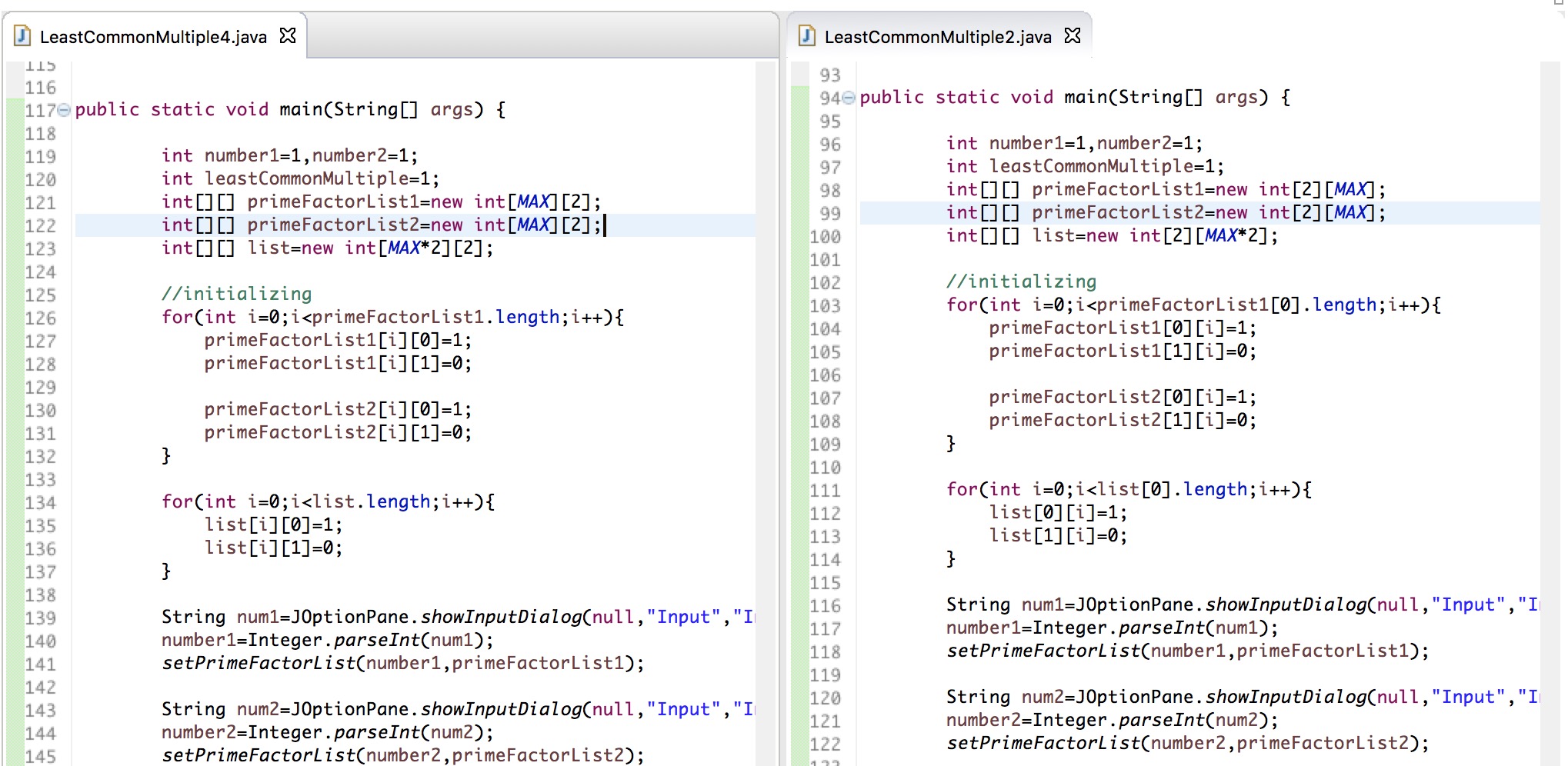 ———-
结束语:
这虽然只是一个小程序,并不是非常难,然而却也反反复复花费了我不少的时间。不经意间想起,偶尔发现一些新的问题(bugs)和心得,在原来的基础上渐渐渐渐通过不断地追问自己是否还能更好的慢慢慢慢的举一反三,收获还是相当大的。在这个折腾的过程中它会潜移默化的锻炼你的思维方式和解决问题的能力。也提高了我编写代码的质量和能力。
就像是科学是无止境的,我想这世界上是没有最好最高最完美的。拿这个练习来说,正如我在代码里注释里写到的,这个程序的形参还可以拓展到0和负数集合里去,那么,又该如何呢?在我目前所掌握的范围内是去使用异常处理机制。限于时间和精力(这是我第一篇技术博客,已经连续写了9个多小时了……),也因为第一次的激动和兴奋,只能写这么多。本人知识与技能还很有限,希望各位大神多多包涵~~如有更好的解决方案欢迎留言讨论。
另外此题附 C++实现一份(目前并没有 以上的Java版本完善,只相当于 LeastCommonMultiple2.java):
LeastCommonMultiple.cpp
//
// LeastCommonMultiple.cpp
// Practices
//
// Created by TTH on 15/7/25.
// Copyright (c) 2015年 TTH. All rights reserved.
//
#include if(pfl[0][i]==f)
break;
else if(pfl[0][i]==1)
{
pfl[0][i]=f;
break;
}
else
continue; //there is a bug on condition that the integer has more than "Max" factors
}
pfl[1][i]++;
n=n/f;
f=2;
}
else
f++;
}
}
}
//search a bigger number betwenn two numbers
int max(int a,int b)
{
if(a>=b)
return a;
else
return b;
}
//output the prime factor list of a integer n
void outputPrimefactorList(int n,int list[][MAX])
{
cout<"factor list of "<" is "<for(int i=0;iif(i==0)
cout<<"factors ";
if(list[0][i]!=1)
cout<<list[0][i]<<" ";
}
cout<for(int i=0;iif(i==0)
cout<<"power ";
if(list[1][i]!=0)
cout<<list[1][i]<<" ";
}
cout<//override the output
void outputPrimefactorList(int n,int list[][MAX*2])
{
cout<"factor list of "<" is "<for(int i=0;i2;i++)
{
if(i==0)
cout<<"factors ";
if(list[0][i]!=1)
cout<<list[0][i]<<" ";
}
cout<for(int i=0;i2;i++)
{
if(i==0)
cout<<"power ";
if(list[1][i]!=0)
cout<<list[1][i]<<" ";
}
cout<int calculteLCM(int pfl1[][MAX],int pfl2[][MAX],int list[2][MAX*2])
{
int lcp=1;
int l=0;
//scan the fommer prime factor list
for(int i=0;iint j=0;
for(;jif(pfl1[0][i]==pfl2[0][j])
break;
}
list[0][l]=pfl1[0][i];
if(j==MAX)
list[1][l]=pfl1[1][i];
else
list[1][l]=max(pfl1[1][i],pfl2[1][j]);
l++;
}
//scan the latter prime factor list
for(int j=0;jint i=0;
for(;iif(pfl2[0][j]==pfl1[0][i])
break;
}
if(i==MAX)
{
list[0][l]=pfl2[0][j];
list[1][l]=pfl2[1][j];
l++;
}
}
for(int i=0;ipow(list[0][i],list[1][i]);
return lcp;
}
int main()
{
int number1,number2;
cout<<"input two integer"<cin>>number1>>number2;
int pfl1[2][MAX];
int pfl2[2][MAX];
//make up a prime factor list for the least common multiple
int lcp;
int list[2][MAX*2];
//initialize the prime factor list
for(int i=0;i2;i++)
{
list[0][i]=1;
list[1][i]=0;
}
for(int i=0;i0][i]=pfl2[0][i]=1;
pfl1[1][i]=pfl2[1][i]=0;
}
primeFactorList(number1,pfl1);
primeFactorList(number2,pfl2);
lcp=calculteLCM(pfl1,pfl2,list);
//output the factor list4
outputPrimefactorList(number1,pfl1);
outputPrimefactorList(number2,pfl2);
cout<<"\nthe least common mutiple of "<" and "<" is ";
cout<list);
return 0;
}
//
// isPrime.h
// Practices
//
// Created by TTH on 15/7/25.
// Copyright (c) 2015年 TTH. All rights reserved.
//
#ifndef Practices_isPrime_h
#define Practices_isPrime_h
#endif
#includereturn false;
}
int i=2;
for(;i<=integer;i++)
{
if(integer%i==0)
break;
}
if(i==integer)
return true;
else
return false;
} 写于2015.10.5.05.56 10h