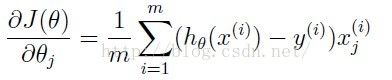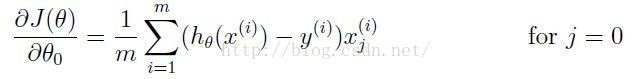Coursera_Stanford_ML_ex2_Logistic Regression 作业记录
ProgrammingExercise 2: Logistic Regression
这周总结一下Week3的作业,使用Logstic回归对数据集中的两个类别进行分类并画出决策边界。总体来说并没有太大的难度,但是要在细节上面多留心。首先看一下作业要求:
除了打星号的以外,我还建议大家再看一下不带星号的文件,可以更好的帮助我们更好的理解Logstic算法的实现,现在先开始主要部分的实现。
一.Ex2
plotData.m目的是将不同类别的数据找出来,用plot进行数据可视化。让我们先观察一下数据,类别已经给出,所以直接找到对应的Score就行。
| Exam1_Score |
Exam2_Score |
Class |
| 35.84740876993872 |
72.90219802708364 |
0 |
| 60.1825993862097 |
86.30855209546826 |
1 |
pos = find(y==1); neg = find(y == 0);% Find Indices of Positive and Negative Examples
plot(X(pos, 1), X(pos, 2), 'k+','LineWidth', 2, 'MarkerSize', 7);
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'y', 'MarkerSize', 7);效果如下:
Sigmoid.m要求给出Sigmoid函数:
g=1./(1+exp(-z)); 现在的我只能理解用这个函数目的在于把通过拟合得到的方程的值控制在[0,1]这个范围内,可能还有别的含义我没有领悟,让我们看一下函数图像: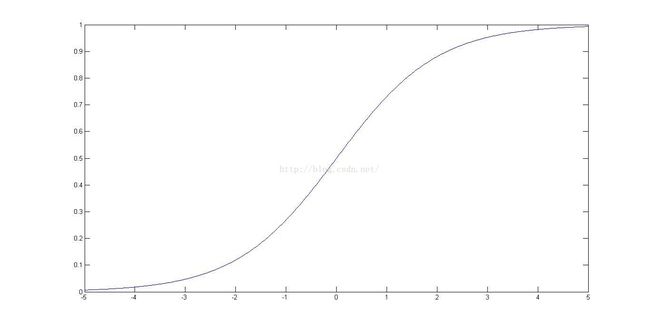
CostFunction.m要求写出误差函数和梯度函数
误差函数:
用矩阵运算实现:
J=(-log(sigmoid(theta'*X'))*y-log(1-sigmoid(theta'*X'))*(1-y))/m;梯度函数
grad=X'*(sigmoid(theta'*X')'-y)/m;效果如下(误差0.693147):
二.Ex2_reg
可以看到无法用线性的决策边界将两类别完全分开,所以我们尝试加入更多的多项式项。mapFeature.m中使用了x1,x2构成的六次多项式 :
为了避免过拟合,需要在误差函数和梯度函数中加入正则化项:
利用矩阵运算实现时注意![]() 不要引入正则化项,原因视频中有讲:
不要引入正则化项,原因视频中有讲:
J=(-log(sigmoid(theta'*X'))*y-log(1-sigmoid(theta'*X'))*(1-y))/m+...lambda*(theta(2:size(theta,1),1)'*theta(2:size(theta,1),1))/2/m;
grad(1,1)=X(:,1)'*(sigmoid(theta'*X')'-y)/m;
grad(2:size(theta,1),1)=X(:,2:size(theta,1))'*(sigmoid(theta'*X')'-y)/m+theta(2:size(theta,1),1)*lambda/m;
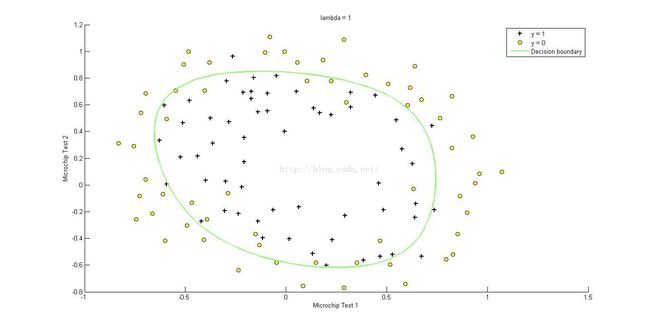
效果如下(误差0.693147,![]() )
)
决策边界是Sigmoid函数值为0时对应x1,x2形成的曲线。