快速排序与随机化快排运行速度实验比较

目录

快速排序与随机化快速排序. 2

快速排序. 2

随机化快速排序. 3

快排与随机化快排性能分析. 4

不同配置的计算机运算效果. 4

不同初始序列对快速排序的影响. 7

数据相对于其多运算的平均值的波动. 11

总结. 13

问题与不足. 13

参考文献. 13

快速排序与随机化快速排序

在计算机科学与数学中，一个排序算法（英语：Sorting algorithm）是一种能将一串数据依照特定排序方式进行排列的一种算法。最常用到的排序方式是数值顺序以及字典顺序。有效的排序算法在一些算法（例如搜索算法与合并算法）中是重要的，如此这些算法才能得到正确解答。排序算法也用在处理文字数据以及产生人类可读的输出结果。基本上，排序算法的输出必须遵守下列两个原则：

1、       输出结果为递增序列（递增是针对所需的排序顺序而言）

2、       输出结果是原输入的一种排列、或是重组

虽然排序算法是一个简单的问题，但是在计算机数据处理上发挥了很大的作用，从计算机科学发展以来，在此问题上也已经有大量的研究。[1]

快速排序

快速排序用到了分治思想，同样的还有归并排序。乍看起来快速排序和归并排序非常相似，都是将问题变小，先排序子串，最后合并。不同的是快速排序在划分子问题的时候经过多一步处理，将划分的两组数据划分为一大一小，这样在最后合并的时候就不必像归并排序那样再进行比较。但也正因为如此，划分的不定性使得快速排序的时间复杂度并不稳定。[2]

快速排序的期望复杂度是O(nlogn)，但最坏情况下可能就会变成O(n^2)，最坏情况就是每次将一组数据划分为两组的时候，分界线都选在了边界上，使得划分了和没划分一样，最后就变成了普通的选择排序了。

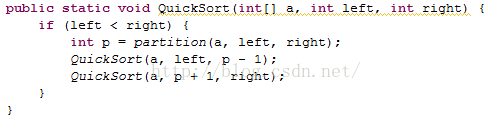
快速排序使用分治法（Divide and conquer）策略来把一个序列（list）分为两个子序列（sub-lists）。

步骤为：

1、从数列中挑出一个元素，称为"基准"（pivot），

2、重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。

3、递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。[3]

 

选定基准：最后一个元素。

排序分区：

递归：

随机化快速排序

当输入序列为有序时，快排的时间复杂度最大，效率最低，为了使快排在任何序列中，效率始终处于最优，引入随机化的思想。随机化即是随机地选择主元，使其运行时间不依赖于输入序列的顺序。

经分析， 随机化快排的算法效率是Θ(nlgn)。

实现：我们只需在选取主元时加入随机因素即可。其他与快排一样。

快排与随机化快排性能分析

不同配置计算机的运行效果

计算机1(简称i7)配置：

硬件：CPU：Intel(R)i7-6500U 2.5GHz，内存：8.00GB

软件：系统：Windows 7专业版 64位操作系统，编译器：eclipse

 

计算机2(简称i3)配置：

硬件：CPU：Intel(R)i3-3110M 2.4GHz，内存：4.00GB

软件：系统：Windows 7旗舰版 32位操作系统，编译器：eclipse

 

实验数据均是取同一数据量100次计算所花时间的平均值

实验结果：

计算机i3数据：

算法	1w	5w	10w	50w	100w	500w	1000w
确定性快排	1	6	11	62	142	777	1611
随机化快排	2	5	13	78	161	877	1815

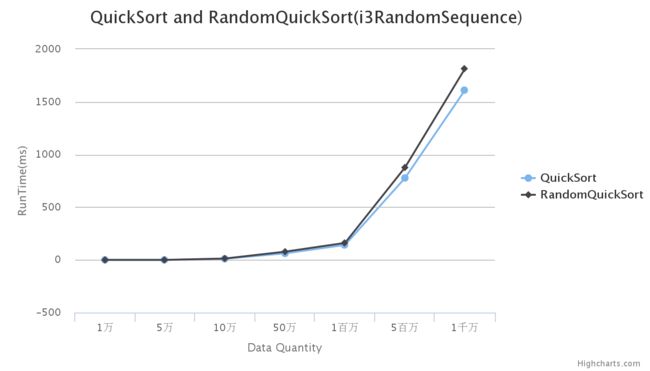
折线图：

从数据与图可以看出，在计算速度上，同一数据量的快速排序中，确定性算法要比随机化算法迅速，而且随着数据量的增大，差距越来越明显。从图中还可以看出，当数据量递增速度慢些时，图形可以近似成一条曲线，该曲线就是它的期望时间复杂度O(nlogn)。

计算机i7数据：

算法	1w	5w	10w	50w	100w	500w	1000w
确定性快排	1	4	10	54	112	655	1240
随机化快排	1	4	11	52	127	644	1389

折线图：

从数据与图可以看到与i3一致的结论，然而i7几乎每一项计算速度都比i3的要快。从图中两条折线中，在数据达到500万时出现明显差距，确定性快排要比随机化快排快很多。查了一些资料，以及老师上课的知识中知道当数据量达到一定程度时，随机化快排要比确定性快排在数据随机的前提下计算速度要快，为了找到那个临界点，我提升了数据的计算量，然而，当数据提到2000万以上时，出现了溢出，Java错误提示：

问题描述
Exception in thread "main" java.lang.OutOfMemoryError: Java heap space

可能原因

你没有为你的应用程序运行时给予足够多的可用内存。

解决方案

增加 JVM堆可用大小，或者减少你的应用程序所需的内存总量。设置jvm heap大小，用eclipse写/调试java程序。在eclipse的配置文件eclipse.ini中设置-vmargs –Xms40m –Xmx800m. [4]

调整后的i7数据可以运行到1亿。

算法	1w	5w	10w	50w	100w	500w	1000w	5000w	10000w
确定性快排	1	4	10	54	112	655	1240	7782	14576
随机化快排	1	4	11	52	127	644	1389	7308	14092

 

    当数据量达到5千万时，随机快排比确定性快排时间要短，速度要快。

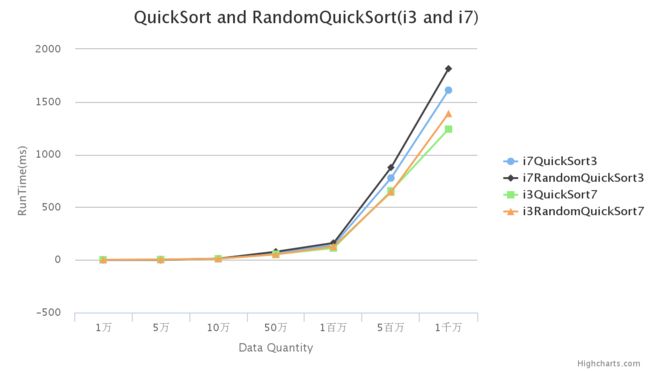
    用同样的方法改进i3时，因为i3内存较小，所以基本没有改变其计算数据量的大小。因此比较i3与i7只比较前面1千万的数据。

    从图中，i7计算速度比i3计算速度快出很多，而且随着计算量的增大，差距越来越明显。所以一个好的软硬件环境对于数据的处理有很大的帮助，反之，则影响处理工作的效率。

不同初始序列对快速排序的影响

         由于初始序列对排序有很大的影响，特别是已经有序的序列对确定性快速排序是其最坏的情况，时间复杂度甚至达到O(n^2)。因此对其初始序列的情况进行专门的实验。

    对初始序列处理为：随机序列、降序序列、升序序列以及重复序列。

    数据：

    注：数据都是对同一数据量生成不同的相关序列进行100次计算得到的下取整平均值。

 

数据量	算法	随机序列	降序序列	升序序列	重复序列
1亿	确定性算法	14576	13915	13679	14282
	随机性算法	14092	5479	4549	13220
7500w	确定性算法	10403	10446	10276	10446
	随机性算法	9631	4361	3406	9639
5000w	确定性算法	7782	6618	6723	6733
	随机性算法	7308	2250	2263	6240
2500w	确定性算法	3262	3296	3218	3268
	随机性算法	3061	1315	1101	3039
1000w	确定性算法	1240	967	1272	1243
	随机性算法	1389	414	547	1193
750w	确定性算法	916	951	904	917
	随机性算法	871	383	395	859
500w	确定性算法	655	614	644	581
	随机性算法	644	219	288	547
250w	确定性算法	289	298	281	280
	随机性算法	274	133	129	270
100w	确定性算法	112	109	109	108
	随机性算法	127	40	50	104
75w	确定性算法	79	81	79	81
	随机性算法	76	29	28	75
50w	确定性算法	54	52	49	49
	随机性算法	52	19	16	50
25w	确定性算法	24	25	24	23
	随机性算法	24	12	10	23
10w	确定性算法	10	9	9	7
	随机性算法	11	3	3	13
7.5w	确定性算法	7	7	7	6
	随机性算法	7	3	3	6
5w	确定性算法	4	4	4	5
	随机性算法	4	1	1	3
2.5w	确定性算法	1	2	2	3
	随机性算法	2	1	0	2
1w	确定性算法	1	0	0	0
	随机性算法	1	0	0	0

   

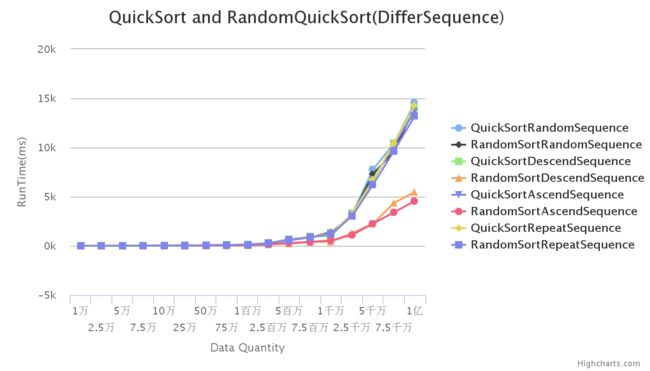
折线图：

    可以看出厨师序列的随机序列与重复序列基本一致，快速排序的随机性算法在初始有序的情况下效率非常高。为了看得更清楚，我们分开对比。

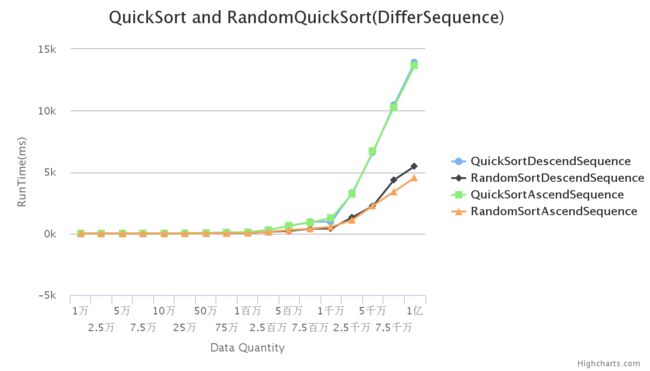
    初始序列为降序序列与升序序列的对比：

    由图可以看出在初始序列有序的情况下，随机化算法比确定性算法快很多，效率更高，而且随着数据量的增大，差距越来越明显。而确定性算法随着数据量的增长其计算时间呈指数增长，效率很差，时间复杂度达到最坏情况的O(n^2)。

    初始序列为降序的随机性快排算法在数据量达到5千万到1亿之间，其排序所耗时间要比升序的随机性快排算法要多，效率要低。而确定性算法不管升序还是降序，其计算时间基本一致。

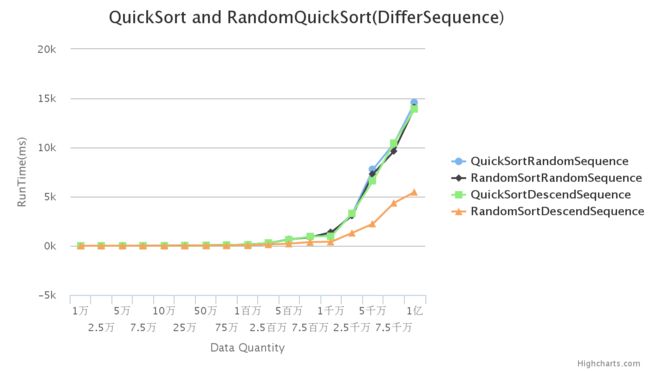
    初始序列为随机序列与降序序列的对比：

    初始序列为随机序列与降序序列其在确定性算法中曲线基本重叠，数据一致，但是在初始有序的前提下，随机化算法运算时间大大减少，效率越来越高。

    因为降序与升序曲线基本一致，就不对比随机序列与升序序列了。

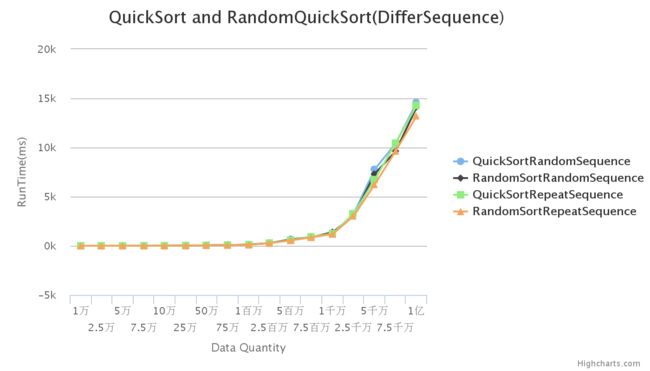
    初始序列为随机序列与重叠序列的对比：

注：重叠序列的处理：重叠的实现是将要实现的数据量分成10个组，然后将其中一个组随机生成数据，然后将该组数据逐一复制到其他组中，这就形成了有10组数据的重复。

    由图，曲线基本重合，因此数据重复对快速排序基本没有影响。

数据相对于其多运算的平均值的波动

我们取数据时，一般是取其同一数据量大小，不同随机生成序列的多次运算的平均时间，然而其单次运算的时间相对于其多次的平均时间波动如何呢？我研究了一下。

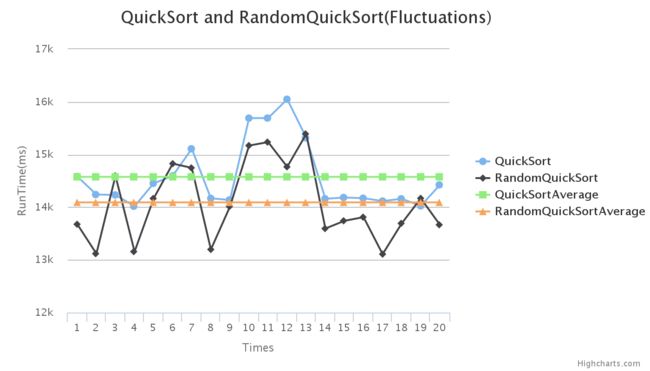
这是数据量为1百万的波动图（i7随机序列数据）

    其时间数据相对于平均数（-3，+8）之间波动。

    我们看大数据：下面是数据量为1亿的波动

    其波动范围达到了（-880，+1500），波动越来越大，越来越明显。

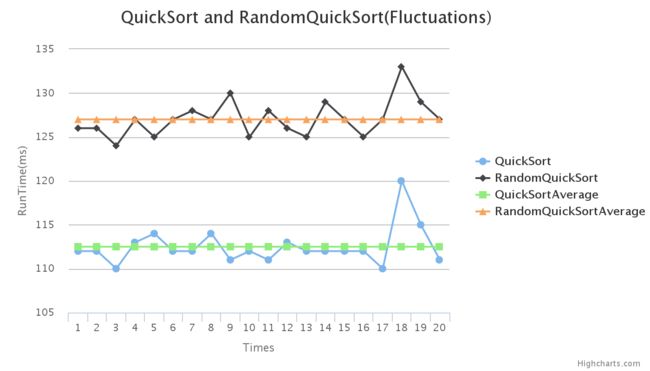
    对比其数据量对其单个数据的平均值波动影响：

    上面画出的较为明显的1百万的数据波动图在这个集合图中只能显示出一条直线，1千万的数据量也成了一条直线（蓝黑“直线”），当数据量为5千万时，出现了波动，但也不太明显，只有1亿的数据量才有明显清晰的波动情况。因此，数据量越大，其单个数据相对于其多次运算的均值波动更为强烈。在数据处理中，其具体取值在数据量越来越大的情况下显得尤为重要。

总结

    这篇文章是我研一来的第一篇文章，以前在CSDN上只看别人的，现在我觉得我有必要自己写一些东西，来记录一下我的学习过程，对自己也是一个交代。希望以后能继续写自己原创的博文。这篇参考了一些大牛的作品，下面都有参考文献。如果我的作品有幸被别人引用时，也希望你能够标注一下，这是一个好习惯，谢谢。

    下面是我提交的作业的总结。

    因为之前没有做过此类的研究，所以当老师将此作业交代下来后，不知所措，不知道怎么分析与画图。之后在网络资料、师哥们的热心帮助与同学们的相互讨论中渐渐有了眉目，对于自己要做的事情有了清晰的目标。

    相对于怎么来对比确定性快排与随机化快排，老师也给了很多入手的方向，包括它的初始序列特点、相关论文的介绍、优化方法等。我自己选了针对不同频率处理器与不同大小内存的计算机进行运算比较；针对其随机、降序、升序与重复的初始序列进行排序时间比较；针对每次运算相对于其多次运算均值的波动情况分析。在这些分析与数据处理中，学到了很多知识，知道了一个算法优劣的具体比较过程，对以后论文及其他方面能力的学习与提升有很大的帮助。

    总体来说，配置较好的机器能更快速地处理数据；数据量在5千万到1亿之间（1亿以上数据量运行不出），初始为随机的序列，用随机化算法耗时低于确定性算法，5千万数据量以下基本高于确定性算法；初始有序对于确定性算法处于最坏的情况，耗时最长，随机化算法反之；数据量越大单个数据对于其多次计算均值波动越大。

问题

         原本想处理不同编译器对于其快速排序与随机化快排的影响，但是当我想做这个时，下载编译软件（刷了系统，无此软件）耗时太长，网速太差，就此作罢。

       问题：

1、同一数据量i3上面会出现有计算结果0的情况，i7不会出现，这是什么情况？

2、9 4 5 4 5 5 5 4 5 4 5 55 4 5 5 5 4 5 4前期大后期稳定？在序列中很多次出现前面数据先计算的数据相对后面的序列要大。

3、均值下取整会影响平均值？当数据量小时，会出现平均值小数情况，其上下取整都会影响其均值，进而影响其波动情况。

4、到微秒的整算，数据小时误差较大？

 

参考文献

---

[1] 维基百科，排序算法https://zh.wikipedia.org/wiki/%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95，2016/10/31

[2] Hamster博客，CSND，算法导论（一）：快速排序与随机化快排，http://blog.csdn.net/haelang/article/details/44496387，2016/10/31

[3] 维基百科，快速排序https://zh.wikipedia.org/wiki/%E5%BF%AB%E9%80%9F%E6%8E%92%E5%BA%8F，2016/10/31

[4] 知足常乐博客，http://tscfengkui.blog.51cto.com/2204656/623458，2016/10/31

老师修改意见

     老师在课上对大家作业进行了点评，具体意见总结如下：（不一定是特定本文章的问题，具体的我还没有修改，先记录一下吧，不然很快忘了）

1 图表都要写表名与图名，表名在表上，图名在图下

2 图表要居中，编号要有序

3 以后发表论文可能是黑白印刷，所以要注意自己的图表除了颜色区分外还要有具体形状或标注区分

4 图的波动要明显，注意自己的单位长度的设定

5 文章错别字一定要注意，不然会影响自己在投稿期刊审稿人的印象

6 此篇文章还可以考虑在双核四核等不同处理器下编程实现高效率计算

7 精度要确定好，单位要标注

8 变量斜体

9 图形布局一般把说明放在图中，减少空间

10 均值计算，去掉最高与最低进行平均