python基础: 遍历与八皇后问题浅析

遍历思想与八皇后问题

      作为对《python基础教程》关于八皇后一节的补充说明，本文旨在使人从直觉上理解八皇后及其相关问题更进一步。
      在固定大小的棋盘上，n个皇后所有的排列组合个数是有限的, 思路极为清晰: 在这有限个组合中剔除所有不满足要求的组合，剩下的就是答案。

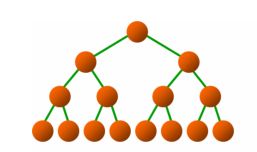
      如图，在树的遍历中，每一个从根节点到达叶子的路径，就是一个解。

用python解决八皇后

步骤:

 1. 判断皇后冲突
 2. 递归得到结果
 3. 输出所有结果

关于皇后冲突的判定

     用自然语言很容易描述八个皇后的位置制约关系，即棋盘的每一行，每一列，每一个条正斜线，每一条反斜线，都只能有1个皇后。如果用这个方法，判断新加入的皇后位置是否与已经存在的皇后位置冲突，先求出新皇后在哪一行，列，正反两条斜线上，再依次判断是否冲突。也不是不可以，不过实现起来较复杂又不简洁。

     观察以下棋盘及每个位置坐标；

1. 发现以下规律:
2. 在同一 ‘/’ 斜线上的位置，横纵坐标之 和 相同

3. 在同一 ‘\’ 斜线上的位置，横纵坐标之 差 相同

   由此可以很轻松的判断新皇后在正反两条斜线上是否与已经存在的皇后们的坐标冲突。

判定冲突函数

1. 参数1: 之前做出的选择构成的序列(列表或元组)

2. 参数2: 当前选择

3. 函数目的: 判断当前选择是否与之前的选择冲突
   关于判断冲突函数的写法，分两类，一种是分析棋盘上所有的棋子是否冲突，而另一种则是默认之前的棋子间不会冲突，而判断当前要检验的新棋子是否与之前的每一个棋子冲突。明显第二种实现更为简洁。
   下面是冲突的判定函数

def confict(state, pos):
    nextY = len(state)
    if pos in state: return True
    '''判断斜线'''
    for i in range(nextY):
        if nextY-pos == i-state[i]: return True
        if nextY+pos == i+state[i]: return True
    return False

递归“函数”

上面的冲突判定函数不难理解，但下面的“函数”对程序初学者来说可能就要费一些周折。

def queens(num, state=()):
    if num-1 == len(state):
        for i in range(num):
            if not confict(state, i):
                yield (i,)
    else:
        for pos in range(num):
            if not confict(state, pos):
                for result in queens(num, state+(pos,)):
                    yield (pos,) + result


for i in list(queen首先看参数

首先看参数
  参数num皇后个数，第一个参数num是皇后个数，也是棋盘共num行num列。第二个参数是之前皇后的位置。 首先代码分为两部分，即if 中的内容 和 else 中的内容。
如果当前选择是最后一步, 遍历这一步能做出的所有选择，挑选出那些符合我们定义的选择。我们好像不试图从头解决这个问题，而是直接跳到最后一步来。

     如果当前选择不是最后一步，那么依然遍历所有选择，当然因为不是最后一步，当前选择的可取性受制于之前的选择，并且限制了之后的选择。目光短浅的看，我们知道一些选择现在看来是合理的，但是不知道如果我们真的做此选择，会不会让后面的选择举步维艰。但是无论如何，我们只是做出当前来看可以得选择，即使后面推出当前的选择是错的，也无可厚非，因为我们正事通过这样排除所有根本不可能的，剩下的就是结果了。
    先看第一个”if”代码块，代码含义显而易见，如果只剩下最后一个皇后要放置了，那么遍历棋盘上最后一行的所有位置，将符合条件的位置输出。
   第一个”if”并不难，但大多初学者会被第二个”else”里的嵌套循环弄得略晕。看”else”中第一个”for”语句，没错，还是遍历当前行的所有位置，(因为第一行放皇后，第二行放皇后，第三行放皇后。。。，恰好到不是最后一行的当前行)。好吧，大多初学都被第二个”for”代码块弄晕了，yield的那个又是什么东西?
    先大概说下“yield，它类似于return,但和return不同的是return 返回一个值(这个“值”可以是数值，字符串，序列等，但只是一次一个)，然后函数就结束了，而yield某个值后函数不会结束，而是继续找出接下来所有符合条件的值，然后才结束。关于yield还有疑问, 百度或任何一本python基础教程书都会告诉你的。（好吧，如果非要吹毛求疵的话，含有yield的“函数”叫做生成器: )）
  “yield (pos,) + result”, “pos”是当前行不与之前的皇后们冲突的位置，本质是取值0-7的整型，而在小括号里的pos再加上一个“，”表明(pos,)是只有一个元素的元组，而result也是元组，元组无法和数值类型的想家，而这就是它们可以相加的原因。
  用yield而不用return的目的是我们想得到八皇后的所有位置的情况。这个”for”代码块的意思就是:
    如果pos这个位置可以放皇后，那么就把它放上，在此基础上，得到接下来一行行找位置把皇后放下去的所有正确结果。

最后输出所有情况即可

for i in list(queens(8)):
    print i

八皇后问题模板与应用

接下来总结这个通用的模板:

判断冲突函数

conflict(之前的选择序列，当前的选择):
    '''根据具体需要进行判定即可'''
    ……

递归“函数”

foo(之前的选择序列):

    若当前是最后一次选择:
      遍历选择的所有取值:
        此次取值不与之前的选择冲突:
          元组(或列表)形式“返回”该值

    当前不是最后一次选择：
      遍历所有取值:
        不与之前的选择序列冲突:
          “返回”当前选择取该值的基础上，接下来的选择结果。

   适用于解数独，计算某些沙盘游戏的最佳建筑布局，有时间再续。
   本文原以自娱，如有错误或不足，还请指正，莫要贻笑于大方之家。