数据结构及算法:链表相关(如何判断单链表是否存在环、找出入环点、链表相交等问题)
目录
一、如何判断单链表是否存在环
方法一、穷举遍历
方法二、哈希表缓存
方法三、快慢指针(推荐)
方法四、Set集合大小变化
二、如何找出有环链表的入环点?
方法一、用HashSet来解决
方法二、计算循环(快慢指针)
情况一:多走一个环
情况二、当fast比slow 多走n个环
代码实现
三、如果存在环,求出环上节点的个数;
四、如果存在环,求出链表的长度;
五、如果存在环,求出环上距离任意一个节点最远的点(对面节点);
六、如何判断两个无环链表是否相交;如果相交,求出第一个相交的节点
一、如何判断单链表是否存在环
![]()
要求:
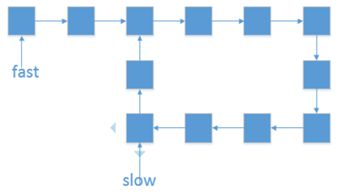
有一个单向链表,链表当中有可能出现“环”,就像题图这样。如何用程序判断出这个链表是有环链表?
- 不允许修改链表结构。
- 时间复杂度O(n),空间复杂度O(1)。
方法一、穷举遍历
首先从头节点开始,依次遍历单链表的每一个节点。每遍历到一个新节点,就从头节点重新遍历新节点之前的所有节点,用新节点ID和此节点之前所有节点ID依次作比较。如果发现新节点之前的所有节点当中存在相同节点ID,则说明该节点被遍历过两次,链表有环;如果之前的所有节点当中不存在相同的节点,就继续遍历下一个新节点,继续重复刚才的操作。
例如这样的链表:A->B->C->D->B->C->D, 当遍历到节点D的时候,我们需要比较的是之前的节点A、B、C,不存在相同节点。这时候要遍历的下一个新节点是B,B之前的节点A、B、C、D中恰好也存在B,因此B出现了两次,判断出链表有环。
假设从链表头节点到入环点的距离是D,链表的环长是S。那么算法的时间复杂度是0+1+2+3+…+(D+S-1) = (D+S-1)*(D+S)/2 , 可以简单地理解成 O(N*N)。而此算法没有创建额外存储空间,空间复杂度可以简单地理解成为O(1)。
方法二、哈希表缓存
首先创建一个以节点ID为键的HashSet集合,用来存储曾经遍历过的节点。然后同样是从头节点开始,依次遍历单链表的每一个节点。每遍历到一个新节点,就用新节点和HashSet集合当中存储的节点作比较,如果发现HashSet当中存在相同节点ID,则说明链表有环,如果HashSet当中不存在相同的节点ID,就把这个新节点ID存入HashSet,之后进入下一节点,继续重复刚才的操作。
这个方法在流程上和方法一类似,本质的区别是使用了HashSet作为额外的缓存。
假设从链表头节点到入环点的距离是D,链表的环长是S。而每一次HashSet查找元素的时间复杂度是O(1), 所以总体的时间复杂度是1*(D+S)=D+S,可以简单理解为O(N)。而算法的空间复杂度还是D+S-1,可以简单地理解成O(N)。
方法三、快慢指针(推荐)
首先创建两个指针1和2(在java里就是两个对象引用),同时指向这个链表的头节点。然后开始一个大循环,在循环体中,让指针1每次向下移动一个节点,让指针2每次向下移动两个节点,然后比较两个指针指向的节点是否相同。如果相同,则判断出链表有环,如果不同,则继续下一次循环。
例如链表A->B->C->D->B->C->D,两个指针最初都指向节点A,进入第一轮循环,指针1移动到了节点B,指针2移动到了C。第二轮循环,指针1移动到了节点C,指针2移动到了节点B。第三轮循环,指针1移动到了节点D,指针2移动到了节点D,此时两指针指向同一节点,判断出链表有环。
此方法也可以用一个更生动的例子来形容:在一个环形跑道上,两个运动员在同一地点起跑,一个运动员速度快,一个运动员速度慢。当两人跑了一段时间,速度快的运动员必然会从速度慢的运动员身后再次追上并超过,原因很简单,因为跑道是环形的。
/**
* 判断单链表是否存在环
* @param head
* @return
*/
public static boolean isLoopList(ListNode head){
ListNode slowPointer, fastPointer;
//使用快慢指针,慢指针每次向前一步,快指针每次两步
slowPointer = fastPointer = head;
while(fastPointer != null && fastPointer.next != null){
slowPointer = slowPointer.next;
fastPointer = fastPointer.next.next;
//两指针相遇则有环
if(slowPointer == fastPointer){
return true;
}
}
return false;
} 假设从链表头节点到入环点的距离是D,链表的环长是S。那么循环会进行S次(为什么是S次,有心的同学可以自己揣摩下),可以简单理解为O(N)。除了两个指针以外,没有使用任何额外存储空间,所以空间复杂度是O(1)。
方法四、Set集合大小变化
还可以用 set 遍历链表,把节点放入set里,每次访问下个节点时,如果set长度不变,则跳出,说明有环。否则set长度+1,继续遍历。
该方法时间复杂度是O(N),空间复杂度上因为需要额外等数量的存储空间,所以空间复杂度是O(n)。
二、如何找出有环链表的入环点?
方法一、用HashSet来解决
public ListNode EntryNodeOfLoop(ListNode pHead){
HashSet hs = new HashSet();
while(pHead!=null){
if(!hs.add(pHead))//如果包含了,那么这个就是入口结点
return pHead;
pHead = pHead.next;
}
return null;
}
方法二、计算循环(快慢指针)
用两个指针,一个fast指针,每次走两步,一个slow指针,每次走一步,当fast指针与slow指针相遇时,假设fast指针走了2x,那么slow指针走了x,由于有环,那么为了便于理解,分为两种情况
情况一:多走一个环
1、当fast指针仅仅只比slow指针多走一个环,如图所示
2、第一次相遇的时候,如图
3、这个时候将fast 重新赋值为开头,如图
4、再走两次,则找到了环的入口结点
重新梳理一下步骤,解题思路
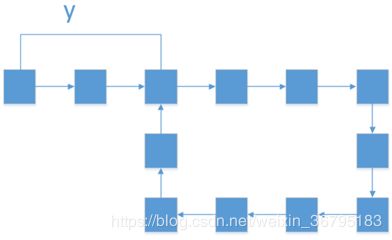
a、第一步,找环中相汇点。分别用fast,slow指向链表头部,slow每次走一步,fast每次走二步,直到fast==slow找到在环中的相汇点。
b、第二步,找环的入口。接上步,当fast==slow时,fast所经过节点数为2x,slow所经过节点数为x,设环中有n个节点,fast比slow多走一圈有2x=n+x; n=x;
可以看出slow实际走了一个环的步数,再让fast指向链表头部,slow位置不变。
假设链表开头到环接口的距离是y,如下图所示,那么x-y表示slow指针走过的除链表开头y在环中走过的距离,那么slow再走y步,此时fast结点与slow结点相遇,fast == slow ,x-y+y=x = n,即此时slow指向环的入口。
情况二、当fast比slow 多走n个环
解题思路
a、第一步,找环中相汇点。分别用fast,slow指向链表头部,slow每次走一步,fast每次走二步,直到fast==slow找到在环中的相汇点。
b、第二步,找环的入口。接上步,当fast==slow时,fast所经过节点数为2x,slow所经过节点数为x,设环中有n个节点,fast比slow多走r圈有2x=rn+x; x=rn;(r为圈数,n为一圈的结点数)
可以看出slow实际走了多个环的步数,再让fast指向链表头部,slow位置不变。
假设链表开头到环接口的距离是y,那么x-y表示slow指针走过的除链表开头y在环中走过的距离,那么slow再走y步,此时fast结点与slow结点相遇,fast == slow ,x-y+y=x = rn,即此时slow指向环的入口。
代码实现
public ListNode EntryNodeOfLoop2(ListNode pHead){
ListNode fast = pHead;
ListNode slow = pHead;
while(fast != null && fast.next != null){
fast = fast.next.next;
slow = slow.next;
//当快指针 与 慢指针相遇时
if(fast == slow){
fast = pHead;
//再次相遇
while(fast != slow){
fast = fast.next;
slow = slow.next;
}
return fast;
}
}
return null;
}三、如果存在环,求出环上节点的个数;
对于这个问题,这里有两个思路(肯定还有其它跟好的办法):
思路1:记录下相遇节点存入临时变量tempPtr,然后让slow(或者fast,都一样)继续向前走slow = slow -> next;一直到slow == tempPtr; 此时经过的步数就是环上节点的个数;
思路2: 从相遇点开始slow和fast继续按照原来的方式向前走slow = slow -> next; fast = fast -> next -> next;直到二者再次相遇,此时经过的步数就是环上节点的个数 。
第一种思路很简单,其实就是一次遍历链表的环,从而统计出点的个数,没有什么可以详细解释的了。
对于第二种思路,我们可以这样想,结合上面的分析,fast和slow没一次操作都会使得两者之间的距离较少1。我们可以把两者相遇的时候看做两者之间的距离正好是整个环的长度r。因此,当再次相遇的时候所经过的步数正好是环上节点的数目。
四、如果存在环,求出链表的长度;
到这里,问题已经简单的多了,因为我们在问题1、2、3中已经做得足够的”准备工作“。
我们可以这样求出整个链表的长度:
链表长度L = 起点到入口点的距离 + 环的长度r;
已经知道了起点和入口点的位置,那么两者之间的距离很好求了吧!环的长度也已经知道了,因此该问题也就迎刃而解了!
五、如果存在环,求出环上距离任意一个节点最远的点(对面节点);
如下图所示,点1和4、点2和5、点3和6分别互为”对面节点“ ,也就是环上最远的点,我们的要求是怎么求出环上任意一个点的最远点。
对于环上任意的一个点ptr0, 我们要找到它的”对面点“,可以这样思考:同样使用上面的快慢指针的方法,让slow和fast都指向ptr0,每一步都执行与上面相同的操作(slow每次跳一步,fast每次跳两步),
当fast = ptr0或者fast = prt0->next的时候slow所指向的节点就是ptr0的”对面节点“。
为什么是这样呢?我们可以这样分析:
如上图,我们想像一下,把环从ptro处展开,展开后可以是无限长的(如上在6后重复前面的内容)如上图。
现在问题就简单了,由于slow移动的距离永远是fast的一般,因此当fast遍历玩整个环长度r个节点的时候slow正好遍历了r/2个节点,
也就是说,此时正好指向距离ptr0最远的点。
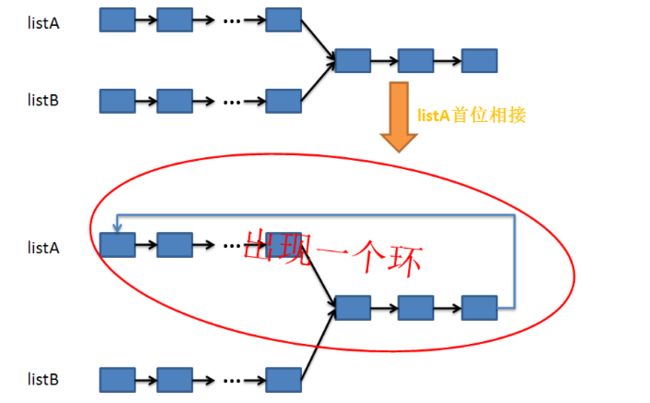
六、如何判断两个无环链表是否相交;如果相交,求出第一个相交的节点
假设有连个链表listA和listB,如果两个链表都无环,并且有交点,那么我们可以让其中一个链表(不妨设是listA)的为节点连接到其头部,这样在listB中就一定会出现一个环。
因此我们将问题6分别转化成了问题1和2.
看看下图就会明白了: