不同的搜索二叉树，不同的二叉搜索树Ⅱ

不同的搜索二叉树

给定一个整u数't no，求以 'i1 ...'n n 为节ng点组成的二叉搜'd索树有多少种？

示例:

输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

思路：主要是明白一个公式，卡特兰数。h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n>=2)。因为计算中用到很多子序列，故DP思想将子序列都存起来。

 

卡特兰数的应用：

    二叉树的计数：已知二叉树有 n 个结点，求能构成多少种不同的二叉树
    括号化问题：一个合法的表达式由()包围，()可以嵌套和连接，如：(())()也是合法表达式，现给出 n 对括号，求可以组成的合       法表达式的个数
    划分问题：将一个凸 n+2 多边形区域分成三角形区域的方法数
    出栈问题：一个栈的进栈序列为1,2,3,..n，求不同的出栈序列有多少种
    路径问题：在 n*n 的方格地图中，从一个角到另外一个角，求不跨越对角线的路径数有多少种
    握手问题：2n 个人均匀坐在一个圆桌边上，某个时刻所有人同时与另一个人握手，要求手之间不能交叉，求共有多少种握手       方法
 

不同的二叉搜索树Ⅱ

给定一个整数 n，生成所有由 1 ... n 为节点所组成的二叉搜索树。

示例:

输入: 3
输出:
[
  [1,null,3,2],
  [3,2,null,1],
  [3,1,null,null,2],
  [2,1,3],
  [1,null,2,null,3]
]
解释:
以上的输出对应以下 5 种不同结构的二叉搜索树：

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

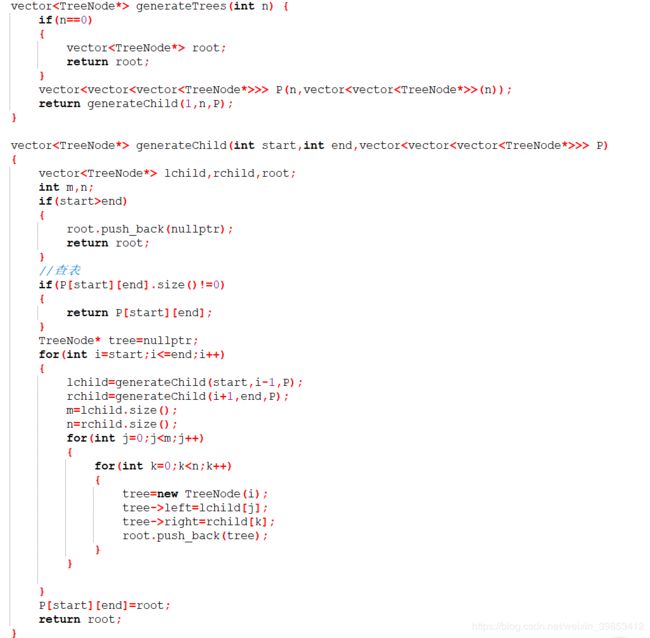
思路：实际上就是去生成二叉搜索树，我们这里采用递归的思想，因为A[1...n]中任意一个节点都可以做根节点，所以我们可以循环遍历出所有节点做根的情况，那么我们取当A[j]做根节点时来处理。A[1...j-1]就是左子树上的节点，A[j+1...n]就是右子树上的节点。而左子树又是A[1...j-1]中节点构成的子树，右子树是A[j+1,n]中节点构成的子树，故可以递归来求。

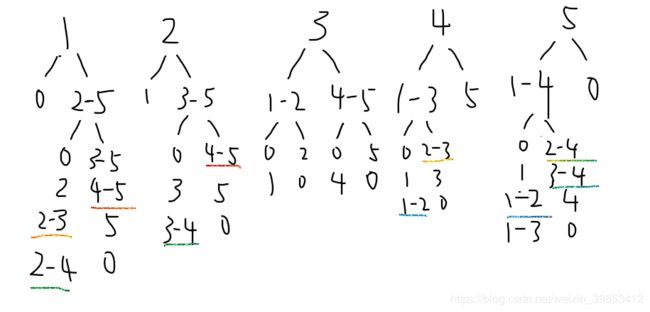
如此递归结果没什么问题，不过效率却并不是最高，因为递归中所求的一些子序列是重复的，这样的话会浪费很多空间和时间，故我们用DP思想来解决这类问题，现在我们来看一下哪里重复了。

这里我并没有分的很细，只是初步分析了一下，我们就发现划线的部分的子序列是重复的，所以我们可以用一个二维数组去存储子序列，每次递归子序列时先去表里查一下是否已有，若有则拿出来用，这样的话时间空间都被省下来了。