通俗讲解支持向量机SVM(四)用尽洪荒之力把核函数与核技巧讲得明明白白(精华篇)
点赞再看,养成习惯,您动动手指对原创作者意义非凡
备战2021秋招面试 微信搜索【CodePan】关注更多新鲜好文和互联网大厂的笔经面经。
作者@试问道
| 当你的才华还撑不起你的野心时,你应该静下心去学习 。 |
|---|
目录
- 前言
- 正文
- 一、高维映射
- 二、什么叫核函数
- 三、只有核函数K的优化问题
- 四、测试样本X流程
- 五、总结
- 1)训练阶段
- 2)测试阶段
前言
之前本系列也有简单提过SVM处理非线性问题,我在这篇文章会用最简单明了的语言讲明白非线性分类问题的解决方法,以及为什么要引入核函数,什么是核技巧,最后会总结一下SVM算法,拎出重点,把脉络梳理清楚。
正文
建议在看这篇之前,把通俗讲解支持向量机SVM(二)对偶性的几何解释 看一下,对SVM的对偶性有一个直观的理解,接下来会顺畅很多。好啦!准备好了吗?耐下心来,咱们开始!
一、高维映射
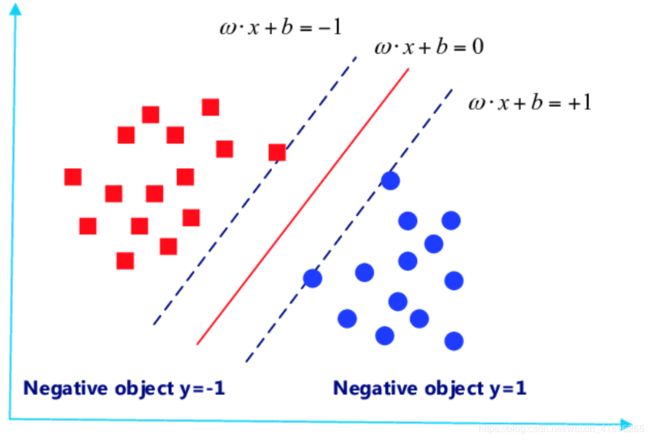
现在我们抛出一个例子,引出问题。先考虑情况一,我们可以很容易的将如上的样本集分类,用一个线性分类器即可。但是如下图的情况二呢?很明显,无法找到一条二维的线性直线将蓝黑两类点分类正确。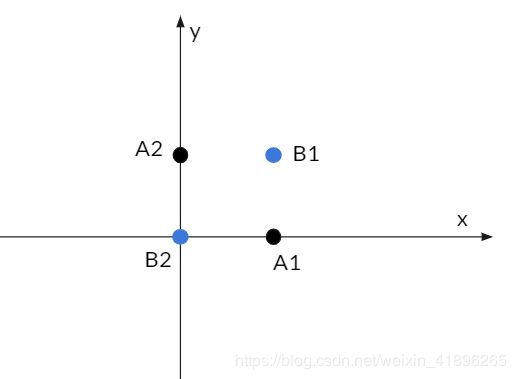
怎么办呢?是的没错!就是用高维映射 φ ( ) \varphi () φ(),我们将二维坐标点A1(1,0),A2(0,1),B1(1,1),B2(0,0)
[ x y ] \left[ \begin{matrix} x \\ y \\ \end{matrix} \right] [xy]
转化到高维空间就可以用直线划分,比如转化为五维坐标点:
φ ( X ) = φ ( A or B ) = [ x 2 y 2 x y x y ] (1) \varphi(X) =\varphi(A \text{or} B) = \left[ \begin{matrix} x^2 \\ y^2 \\ x \\ y \\ xy \\ \end{matrix} \right] \tag 1 φ(X)=φ(AorB)=⎣⎢⎢⎢⎢⎡x2y2xyxy⎦⎥⎥⎥⎥⎤(1)
这样,我们得到转化到五维的四个坐标点,接着,我们再找到一条在五维的直线( ω \omega ω , b)将这四个点分开,以什么为标准呢?参照二维情况,这里我们用:
{ ω T φ ( X ) + b ≥ 1 点X ∈ 类C1 ω T φ ( X ) + b < 1 点X ∈ 类C2 (2) \begin{cases} \omega^T\varphi(X)+b \geq 1& \text{点X} \in \text{类C1}\\ \omega^T\varphi(X)+b < 1& \text{点X} \in \text{类C2} \end{cases} \tag 2 {ωTφ(X)+b≥1ωTφ(X)+b<1点X∈类C1点X∈类C2(2)
注意,我们是以上式为标准,找的一条直线,何谓找到一条直线呢?也就是找到其参数( ω \omega ω , b),找到的参数值为:
ω = [ − 1 − 1 − 1 − 1 4 ] \omega = \left[ \begin{matrix} -1 \\ -1 \\ -1 \\ -1 \\ 4 \\ \end{matrix} \right] ω=⎣⎢⎢⎢⎢⎡−1−1−1−14⎦⎥⎥⎥⎥⎤,以此标准代入参数验证这些坐标点,可以得到 { ω T φ ( A 1 ) + b = 1 点X ∈ 类C1 ω T φ ( A 2 ) + b = 3 点X ∈ 类C1 ω T φ ( B 1 ) + b = − 1 点X ∈ 类C2 ω T φ ( B 2 ) + b = − 1 点X ∈ 类C2 (2) \begin{cases} \omega^T\varphi(A1)+b = 1& \text{点X} \in \text{类C1}\\ \omega^T\varphi(A2)+b = 3& \text{点X} \in \text{类C1} \\ \omega^T\varphi(B1)+b = -1& \text{点X} \in \text{类C2}\\ \omega^T\varphi(B2)+b = -1& \text{点X} \in \text{类C2} \end{cases} \tag 2 ⎩⎪⎪⎪⎨⎪⎪⎪⎧ωTφ(A1)+b=1ωTφ(A2)+b=3ωTφ(B1)+b=−1ωTφ(B2)+b=−1点X∈类C1点X∈类C1点X∈类C2点X∈类C2(2),看!如此,我们很清楚的将在二维平面难以线性划分的样本集在五维平面上线性划分开来了,perfect!那说明什么呢?
事 实 上 , 任 何 样 本 集 如 果 利 用 高 维 映 射 φ ( ) {\color{red} 事实上,任何样本集如果利用高维映射}\varphi() 事实上,任何样本集如果利用高维映射φ() 转 化 到 无 限 维 上 都 可 以 线 性 划 分 开 ! ! ! {\color{red} 转化到无限维上都可以线性划分开!!!} 转化到无限维上都可以线性划分开!!!
二、什么叫核函数
看上面想的多完美,对于任意线性不可分的样本集,我们只要找到高维映射 φ ( ) \varphi() φ()就都可以在高维空间上划分开了,但是吧,事实是这个 φ ( ) \varphi() φ()并不都像上面那个例子那么容易求出来,有时是非常困难的,所以呀,我们引出了核函数(kernal function):
K ( X 1 , X 2 ) = φ ( X 1 ) T φ ( X 2 ) K(X_1,X_2) = \varphi(X_1)^T \varphi(X_2) K(X1,X2)=φ(X1)Tφ(X2)我们直接给出了核函数的形式,现在肯定有些难以理解,没关系,只要清楚核函数就是两无限维向量的内积而已,我们现在要记住我们的目的就是: 在 计 算 过 程 中 用 这 个 已 知 的 核 函 数 来 代 ! 替 ! {\color{red} 在计算过程中用这个已知的核函数来代!替!} 在计算过程中用这个已知的核函数来代!替! 难 以 确 定 的 、 “ 虚 无 的 ” 的 高 维 映 射 函 数 φ ( ) {\color{red} 难以确定的、“虚无的”的高维映射函数\varphi()} 难以确定的、“虚无的”的高维映射函数φ(),由此,我们在这里总结出SVM算法最大的创意点——核技巧(Kernal Trick):我们在做分类问题的时候,可以不清楚无限维映射 φ ( ) \varphi() φ()的显示表达,只要知道核函数 K ( X 1 , X 2 ) K(X_1,X_2) K(X1,X2),那么这个优化问题仍然可解! Min 1 2 ω T ω + C ∑ i = 1 N ζ i (3) \text{Min}\,\,\,\,\, \frac{1}{2} \omega^T\omega +C\sum_{i=1}^{N} \zeta_i \tag 3 Min21ωTω+Ci=1∑Nζi(3) Subject to: y i ( ω T X + b ) ≥ 1 − ζ i , ζ i ≥ 0 \text{Subject to:} y_i(\omega^TX+b) \geq 1-\zeta_i,\,\,\,\,\,\zeta_i \geq 0 Subject to:yi(ωTX+b)≥1−ζi,ζi≥0 (对于这个优化式的来由不清楚的可以查看文末链接)。
三、只有核函数K的优化问题
好啦!先喘一口气,我们总结一下,你看上面核函数的表达式,等号左边实际上是一个变量值,而等号右边是两无限维向量的内积,我们前面做的工作实际上就是引入了核函数,这里有个误区,核函数不是将低维度样本集线性不可分划分的方法,高维映射才是,核函数只是简化了这个过程,我们不需要去求解 φ ( X ) \varphi(X) φ(X)的具体形式而已!(这里有几个关于常用核函数和核函数的举例,你一看就明白了)那么为什么引入核函数呢,没错,借助它,避开 φ ( X ) \varphi(X) φ(X),解以上优化问题!准备好了吗,耐心看下去,我们接着解出上面的优化问题。

首先,为了后续求导方便,我们把 ζ \zeta ζ设为小于等于零,所以上述优化式改写为: Min 1 2 ω T ω − C ∑ i = 1 p i c c e n t e r N ζ i (4) \text{Min}\,\,\,\,\, \frac{1}{2} \omega^T\omega - C\sum_{i=1}^{pic_centerN} \zeta_i \tag 4 Min21ωTω−Ci=1∑piccenterNζi(4) Subject to: 1 + ζ i − y i ( ω T φ ( X ) + b ) ≤ 0 \text{Subject to:\,\,\,} 1+\zeta_i -y_i(\omega^T\varphi(X)+b) \leq 0 Subject to:1+ζi−yi(ωTφ(X)+b)≤0 ζ i ≥ 0 \zeta_i \geq 0 ζi≥0 (这个部分很好理解, ζ \zeta ζ前加上负号就ok了)。
我们设 D = 1 + ζ i − y i ( ω T φ ( X ) + b ) D = 1+\zeta_i -y_i(\omega^T\varphi(X)+b) D=1+ζi−yi(ωTφ(X)+b),那么这个原问题的对偶问题(dual problem)为(目标函数用了拉格朗日函数,引入了参数 α i 和 β i \alpha_i 和 \beta_i αi和βi):
Maxmize Θ ( α i , β i ) = inf 对 于 所 有 ω , b , ζ { 1 2 ω T ω − C ∑ i = 1 N ζ i + ∑ i = 1 N β i ζ i + ∑ i = 1 N α i D } \text{Maxmize} \,\Theta(\alpha_i,\beta_i) = \inf_{对于所有\omega,b,\zeta}\left\{\frac{1}{2} \omega^T\omega - C\sum_{i=1}^{N} \zeta_i + \sum_{i=1}^N\beta_i\zeta_i+\sum_{i=1}^N\alpha_iD\right\} MaxmizeΘ(αi,βi)=对于所有ω,b,ζinf{21ωTω−Ci=1∑Nζi+i=1∑Nβiζi+i=1∑NαiD}
Subject to: α i ≥ 0 \text{Subject to:\,\,\,}\alpha_i \geq 0 Subject to:αi≥0 β i ≥ 0 , i = 1 到 N \beta_i \geq 0,\, i=1到N βi≥0,i=1到N
免得有人在这里犯糊涂,我在这里多唠叨几句,D表明已知有N个样本点(X,yi),我们要做的就是通过这个优化问题在所有的 ω , b , ζ \omega,b,\zeta ω,b,ζ中找到最优的那三个值,怎么算最优,就是这里最大化到什么程度,怎么求出这个值呢?套路!求导呗!
∂ Θ ∂ ω = 0 − − − − − − > ω = ∑ i = 1 N α i y i φ ( X i ) \frac{\partial \Theta}{\partial \omega} = 0 ------>\omega=\sum_{i=1}^{N}\alpha_iy_i\varphi(X_i) ∂ω∂Θ=0−−−−−−>ω=i=1∑Nαiyiφ(Xi) ∂ Θ ∂ ζ = 0 − − − − − − > α i + β i = C (5) \frac{\partial \Theta}{\partial \zeta} = 0------>\alpha_i + \beta_i = C \tag 5 ∂ζ∂Θ=0−−−−−−>αi+βi=C(5) ∂ Θ ∂ b = 0 − − − − − − > ∑ i = 1 N α i y i = 0 \frac{\partial \Theta}{\partial b} = 0------>\sum_{i=1}^{N}\alpha_iy_i=0 ∂b∂Θ=0−−−−−−>i=1∑Nαiyi=0我觉得大家都明白,求导比较繁琐,但肯定不难,稍耐心,肯定能得出正确结果,大家不妨算一算,看看和给出的结果是否一致。
所以,依照求导的结果代入后获得的应该是下确界的值,在maxmize它,再次改写优化问题,约掉 β \beta β,用的是(5)式:
Maxmize Θ ( α i ) = ∑ i = 1 N α i − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j K ( X i , X j ) \text{Maxmize} \,\Theta(\alpha_i) =\sum_{i=1}^N\alpha_i-\frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_jK(X_i,X_j) MaxmizeΘ(αi)=i=1∑Nαi−21i=1∑Nj=1∑NαiαjyiyjK(Xi,Xj)
Subject to: 0 ≤ α i ≤ C \text{Subject to:\,\,\,}0 \leq \alpha_i \leq C Subject to:0≤αi≤C ∑ i = 1 N α i y i = 0 \sum_{i=1}^{N}\alpha_iy_i=0 i=1∑Nαiyi=0 ,再次分析一波,上式中yi,yj是label,已知的值。核函数K则是一开始用户确定采用的那一种核函数(比如常见的高斯核函数和多项式核函数等),而待求的则是 α i , α j \alpha_i,\alpha_j αi,αj,细心的朋友可能已经发现了,优化问题中的 φ ( X ) \varphi(X) φ(X)都慢慢“消失”,被核函数K(X1,X2)代替,这就是前面我们折腾半天的原因, 避 开 φ ( X ) , 用 K 代 替 , 这 也 是 全 篇 的 核 心 所 在 ! ! ! ! ! {\color{red} 避开\varphi(X),用K代替,这也是全篇的核心所在!!!!!} 避开φ(X),用K代替,这也是全篇的核心所在!!!!!
四、测试样本X流程
OK,整理清楚思路,这个问题就很好解了,回归文章开头,我们在测试样本属于哪一类时,用的标准是 { ω T φ ( X i ) + b ≥ 1 y i = + 1 ω T φ ( X i ) + b < 1 y i = − 1 (6) \begin{cases} \omega^T\varphi(X_i)+b \geq 1& y_i=+1\\ \omega^T\varphi(X_i)+b < 1& y_i=-1 \end{cases} \tag 6 {ωTφ(Xi)+b≥1ωTφ(Xi)+b<1yi=+1yi=−1(6)我们一般的思路是求出各个部分在求出结果和1比较,但是如果我们把 ω T φ ( X ) + b \omega^T\varphi(X)+b ωTφ(X)+b当作一个整体就简洁多了。那么这个整体的形式( 避开 φ ( X ) \varphi(X) φ(X),用K代替)最终是什么呢?实际上,经过代入计算可得, ω T φ ( X ) = ∑ i = 1 N α i y i K ( X i , X ) \omega^T\varphi(X) = \sum_{i=1}^{N}\alpha_iy_iK(X_i,X) ωTφ(X)=∑i=1NαiyiK(Xi,X),再次解释一波,这里的(Xi,yi)是已知的训练集样本,而样本X是未知的,我们正是要判断此样本的label值y。
坚持到这里啦!胜利就在前方!现在已经知道 ω T φ ( X ) \omega^T\varphi(X) ωTφ(X)的值,要想知道整体的值,还差一个b,怎么求这个b呢?没错,引出最后一个知识点,KKT条件,要想这个对偶问题的解与原问题相等,需要满足这个KKT条件,即:
对 于 ∀ i = 1 到 N { β i = 0 o r ζ i = 0 α i = 0 o r D = 0 对于\forall i = 1 \text{到} N \begin{cases} \beta_i =0 & or &\zeta_i=0\\ \alpha_i = 0&or & D=0 \end{cases} 对于∀i=1到N{βi=0αi=0ororζi=0D=0
因为约束 0 ≤ α i ≤ C 0 \leq \alpha_i \leq C 0≤αi≤C,则 β i = C − α i > 0 \beta_i = C-\alpha_i > 0 βi=C−αi>0,所以根据KKT条件, ζ i = 0 , and D = 0 \zeta_i=0 ,\text{and} D = 0 ζi=0,andD=0,由此可得出 b = 1 − y i ∑ i = 1 N α j y j K ( X i , X j ) y i b=\frac{1-y_i\sum_{i=1}^{N}\alpha_jy_jK(X_i,X_j)}{y_i} b=yi1−yi∑i=1NαjyjK(Xi,Xj)
五、总结
感谢你一路看到现在,我们对SVM算法做出最后的总结,帮助加深理解:
1)训练阶段
输入样本集(Xi,yi),解优化问题,得到所有的N个 α i \alpha_i αi,并由此得到 β i 和 b \beta_i和b βi和b
2)测试阶段
输入你想要测试的样本X,再根据(6)分类器:
{ ω T φ ( X i ) + b ≥ 1 y i = + 1 ω T φ ( X i ) + b < 1 y i = − 1 \begin{cases} \omega^T\varphi(X_i)+b \geq 1& y_i=+1\\ \omega^T\varphi(X_i)+b < 1& y_i=-1 \end{cases} {ωTφ(Xi)+b≥1ωTφ(Xi)+b<1yi=+1yi=−1进行分类,看吧!问题完美解决了!漂亮的算法!
写到深夜了,但还是为这个美丽的算法所折服,你呢?有收获吗?
| 创作不易,你的鼓励是我创作的动力,如果你有收获,点个赞吧 |
|---|
我接下来还会陆续更新机器学习相关的学习笔记,补充这个系列。如果看到这里的话,说明你有认真看这篇文章,希望你能有所收获!最后,欢迎交流指正!
还有不明白的欢迎阅读其他文章:
通俗讲解支持向量机SVM(一)面试官:什么?线性模型你不会不清楚吧?
通俗讲解支持向量机SVM(二)另辟蹊径!对偶性的几何解释
通俗讲解支持向量机SVM(三)SVM处理非线性问题及软间隔之引出
通俗讲解支持向量机SVM(四)用尽洪荒之力把核函数与核技巧讲得明明白白(精华篇)