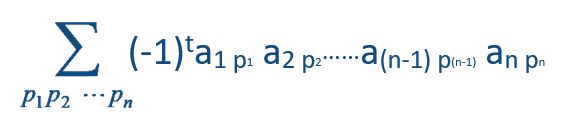全排列，逆序数与行列式的二三事

行列式计算

    在线性代数中，我们接触到了行列式的定义及相关计算，现在我们可以用C语言来帮助我们实现行列式的计算

    一起来把这个顽固的行列式算出来(╯‵□′)╯︵┻━┻

---

行列式计算方式

首先先来回顾一下行列式的计算方式

行列式由定义可知行数和列数相同。对于一个n阶行列式，其行数和列数都是n

a i j 代表行列式中第 i 行第 j 列的元素

 行列式的计算公式

其中 p1p2 ··· pn 为自然数 1, 2, ··· , n 的一个排列，t 为这个排列的逆序数

该公式代表对p1p2 ··· pn所有排列对应的若干项求和，排列数即为项数

那么我们可以将 p1p2 ··· pn 看作n个数在n个数位上进行全排列，然后再执行相应的计算

也就是说，行列式计算需要三步

---

全排列

在之前的排列专题文章中，已介绍了比较法，记录法，交换法三种排列方法，故这里不再多介绍。

由于行列式行数列数相等，所以排列是全排列，且只是计算就不用考虑按序输出排列，因而推荐使用较快的交换法。

 

逆序数

• 比较法

    比较法顾名思义就是按照定义，依次将某数前面的数和它比较大小

#include
void compare(int digit[],int n);

int cnt=0;//用于给逆序数计数 

int main()
{
	int n;
	printf("数的个数："); 
	scanf("%d",&n);
	int digit[n];
	
	printf("数："); 
	for(int i=0;idigit[i]) cnt++;
		}
	}
}

运行效果图

 

• 归并法

归并法利用到了归并排序进行逆序数计算。在之前排序专题的推文中我们已介绍了归并排序。

在这里我们简单回顾一下归并排序的思想。根据分治法的思想，归并排序就是“先分再合”。

先将一个数组无限地一分为二直至不能再分。然后在合并数组的过程中，将每次分割的两个子数组中的元素进行比较，根据顺序依次将元素放到新数组中。重复此步骤直至合并成原来数组的长度。

那么在合并数组过程中的数组元素比较就可以顺便计算逆序数。

#include
using namespace std;

void mergesort(int temp_digit[],int L,int R);

int cnt=0;//用于给逆序数计数 

int main()
{
	int n;
	cout<<"排序的数的个数：";
	cin>>n;
	int temp_digit[n];
	cout<<"准备排序的数：";
	for(int i=0;i>temp_digit[i];
	mergesort(temp_digit,0,n-1);
	cout<<"经排序过的数：";
	for(int i=0;i

运行效果图

 

公式计算

结合全排列，逆序数，公式即可进行行列式计算

下面的代码以交换法实现全排列和归并法实现逆序数计算为例，这样当行列式阶数n较大时，计算速度相对较快

#include

void swap(int *,int*);
void arrange(int [],int [],int [],int,int);
void mergesort(int [],int,int);

int cnt=0;//cnt用于逆序数计数
int term_cnt=0;//term_cnt用于项数计数 
int ans=0;//ans为行列式计算结果

int main()
{
	int n;
	printf("行列式阶数：");
	scanf("%d",&n);
	int digit[n];
	int temp_digit[n];//temp_digit是digit的临时副本，用于给归并法排序来算逆序数 
	int det[n*n];
	//为方便将数组传入函数，用一维数组det存储行列式元素 
	//行列式中i行j列元素为数组det中第i*n+j个元素 
	printf("\n行列式：\n");
	for(int i=0;i

运行效果图

以a（i , j）表示行列式中第 i 行第 j 列元素