排序算法：简单选择排序，堆排序，直接插入排序，二分法插入排序，冒泡排序，快速排序，归并排序

写在前面的声明：本篇博客主要是为了自己以后作回顾之用，所以算法思想上的解释并不细致，代码应该还能算上比较易懂，做了比较多的注释，尤其是比较复杂的堆排序、快速排序、归并排序。每一个排序算法的代码都是本人实验过的，所以应该是可行的。

稳定的排序算法

直接插入排序，二分法插入排序，冒泡排序，归并排序

排序算法的时间复杂度

堆排序，快速排序，归并排序平均时间复杂度为O(nlogn)，算法中默认对数log底数为2，可以写成O(nlog2(n))。

其余的排序算法平均时间复杂度为O（n^2）。

排序算法的辅助空间

快速排序为O（logn）,归并排序O（n），其余排序算法辅助空间为O(1)。

简单选择排序

通过查找从数组中未排序区间寻找到最小元素，来和未排序区间的第一个数据进行位置互换，同时未排序区间的左下标向右移动一个位置。具体代码如下：

#include

//直接选择排序（简单选择排序）
  void sort(int a[],int n)
{
	int temp,k,i;
	for(i=0;ia[j])
			 k=j;
		//如果k=i，说明当前数据为未排序区间的最小数据，不需要更改。
	 if(k!=i)
			{
			temp=a[k];
			a[k]=a[i];
			a[i]=temp;
			}
	}
}
void out(int a[],int n)
{
	cout<<"排序后数组顺序为："<<" ";
	for(int i=0;i<=n-1;i++)
	{		
		cout<

堆排序

第一步构造大根堆：堆排序通过将要排序的数据按照完全二叉树的形式构造，从第一个非叶子结点开始，对当前根结点和子结点的数值作比较，将子结点最大的数据换到根节点，如果根节点的数据最大，就不需要置换，如果根结点和子结点有数据置换，那么需要对被置换的子结点作判断，若此子结点是非叶子结点，需要重新构造堆，若是叶子结点就跳出循环。通过对各个非叶子结点构造大根堆，最后形成所有的根结点都会比子结点大。

第二部置换最大数据到未排序的最大的叶子结点：将最大的根结点（第一个根结点）和最后一个子结点数值互换，同时重新构造大根堆。

具体代码如下：

#include
//堆排序
//交换数据的函数
void swap(int a[],int i,int j)
{
	   int temp1;
       temp1=a[i];
       a[i]=a[j];
       a[j]=temp1;

}
//构造大根堆的函数，index为所在子结点的下标，len为数组的大小
//左子结点的下标为 index*2+1
void heapsort(int a[],int index,int len)
{   //临时变量temp，用来存储子结点中数值较大的下标
	int temp;
//当结点存在左子结点时，就判断子结点和父结点的值大小
	while(index*2+1=0;i--)
	{
		heapsort(a,i,n);
	}
	//将根结点与最后一个结点交换数值，同时重构大根堆
    for(int j=n-1;j>0;j--)
	{
	    swap(a,0,j);
		heapsort(a,0,j);
	}
	out(a,n);

}

直接插入排序

通过从未排序区间第一个数据与已排序区间的数据作比较，找到合适的位置后a[j]后，将a[j]后面的已排序元素分别后移动一个位置，然后，将此数据插入到a[j]。

具体代码如下：

#include
直接插入排序
void insertsort(int a[],int n)
{int temp,j,i;
	for(i=1;i=0&&temp

 

二分法插入排序

二分法插入排序，通过在已排序区间进行二分法查询，找到一个位置可以放置当前变量，然后将此位置后面的已排序数据后移，最后将数据放置到此位置。大致方式和直接查询方式相似，只是寻找可放置的位置采用了二分法。

具体代码如下：

#include
//二分法插入排序
void binaryinsertsort(int a[],int n)
{ 
	int left,right,mid,temp;
	for(int i=1;iright，循环结束，当前变量需要插入的位置是a[left]=a[1]
	//例2：第一次插入 有序区一个变量为2，当前变量为1，left=right=mid=0
    //那么right=mid-1=-1;left>right，循环结束，当前需要插入的位置时a[left]=a[0]
	while(left<=right)
	{
	 mid=(left+right)/2;
	 if(temp=left,需要进行移动
	for(int j=i-1;j>=left;j--)
	a[j+1]=a[j];
	//通过对需要移动的位置下标和当前变量所在的下标进行判断，确定是否需要赋值。如果变量位置没改变，不重复赋值
	if(left!=i)
	a[left]=temp;
	}
}
void out(int a[],int n)
{
	cout<<"排序后数组顺序为："<<" ";
	for(int i=0;i<=n-1;i++)
	{		
		cout<

冒泡排序

冒泡排序，通过相邻两数据的不断比较，将较大的数据置换到未排序区的最后

具体代码如下：

#include
//冒泡排序
void bubblesort(int a[],int n)
{
int temp;
for(int i=n-1;i>0;i--)
for(int j=0;ja[j+1])
	{
	temp=a[j+1];
	a[j+1]=a[j];
	a[j]=temp;
	}
}
}

void out(int a[],int n)
{
	cout<<"排序后数组顺序为："<<" ";
	for(int i=0;i<=n-1;i++)
	{		
		cout<

快速排序

我的基准值设定的是排序区的第一个数据

为了保证和第一个数据置换的数据小于第一个数据，所以先从后往前查询比基准值小的数，再从前往后查询比基准值大的数，然后将这两个数作位置置换，重复此操作直到从后往前的下标和从前往后的下标重合。之后第一个基准值数据和此下标的数据置换。最后将此区间分成了左区间和右区间，左区间都比基准值小，右区间都比基准值大。通过递归调用快速排序算法对两个子区间进行排序。

具体代码如下：

#include
//快速排序
int a[5]={5,5,3,2,4};
//通过递归调用，来实现快速排序算法
//首先确定所要排序的子区间，left为左下标，right为右下标
void quicksort(int left,int right)
{
	//当左下标大于等于右下标时，说明此区间只有一个元素，
	if(left>=right)
	return;
	int i,j;
	i=left;
	j=right;
//用临时变量temp保存区间左边第一个元素	
int temp=a[left];
//当i不等于j时，说明，从后往前和从前往后的排序调整还没有完成
while(i!=j)
{
	//从后往前寻找比第一个数据小的元素
	//因为基准值设定的是左边第一个元素，所以先从后往前找
    //这样能保证最后一步a[i]和a[left]交换后,a[left]=temp&&i

归并排序

我使用的是二路归并排序法

归并主要通过分治法的思想，先对当前要排序的序列，通过递归调用二分法将要排序的序列划分成每一个要排序的区间都只有一个元素，整体形状像一棵二叉树。然后同一层级的相邻两区间进行合并，合并时需要对数值进行比较，将小的数据放置到要合并的区间的前面，不断回归合并最终合并成一个已经排序完整的区间。（归并法的代码是思考了最久才写成功的）

具体代码如下：

#include
//归并排序法
//merge函数用来合并两个区间,需要传递排序的数组a，两个区间的最小下标，中间下标和最大下标
void merge(int a[],int l,int mid,int r)
{
//先输出当前所要合并成的区间的左下标和右下标
cout<<"l的值为："<=la[indexl]&&indexl=la[indexl]&&indexl>=numl)
{
a[k]=ra[indexr];
indexr++;
}
//情况三：右边区间元素值小于左边区间的元素值，并且右边区间的所存放的数据还没有被取完
//a[k]取值右边区间元素
else if(ra[indexr]=numr)
{
a[k]=la[indexl];
indexl++;
}
}
}
//mergesort函数通过递归划分区间，每次从当前区间的中点划分，直到该区间只有一个数
//同时划分完毕之后通过merge函数排序合并已经划分的区间
void mergesort(int a[],int l,int r)
{
if(l>=r)
return;
else
{
int mid=(l+r)/2;
mergesort(a,l,mid);
mergesort(a,mid+1,r);
merge(a,l,mid,r);
}
}
//输出已经排序好的数组
void out(int a[],int n)
{
	cout<<"排序后数组顺序为："<<" ";
	for(int i=0;i<=n-1;i++)
	{		
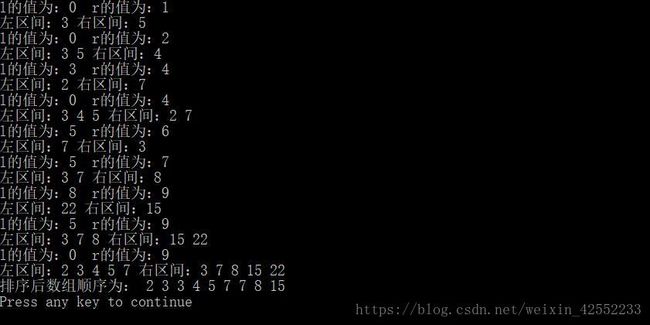
		cout<

最后放上一张归并排序的截图吧！

以上，祝好！