浅谈 线段树 luoguP3372

概念和原理

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。而未优化的空间复杂度为2N，实际应用时一般还要开4N的数组以免越界

其实就是可以在O(nlogn)的时间复杂度内实现区间修改和区间查询

实现

• 首先定义某节点rt的左儿子节点编号为rt>>1,右儿子编号为rt>>1|1(即rt>>1+1)
• 再定义若此节点包含区间 [l,r] ,其左儿子包含区间 [l,(l+r)>>1]，右儿子包含区间 [(l+r)>>1+1,r]
• 最后定义根节点包含区间 [1,n]
  就可以得到类似下图的一棵树
  

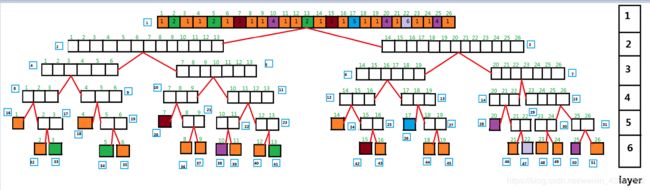
用这种方式存好数组后，我们就可以开始对其进行区间修改和查询了
（由于单点修改和查询是区间修改和查询的子问题，故不再赘述）

区间修改

首先引入一个lazy标记的概念
lazy[i]指i号节点包含的区间被整体操作（加或减等）的累加值
比如说3号节点的区间被整体加上了5，lazy[3]=5
于是当我们要对一段区间进行整体操作修改时，不必将整个区间以O(n)的复杂度修改，只需要以O(1)的复杂度将其lazy标记维护好即可，若操作的区间不能够被某一个点完全覆盖，就将这个区间拆分成几个可以被某几个点所代表区间完全覆盖的区间，再进行操作

当然，维护好lazy标记的同时，我们也要维护好原来需要维护的值。比如说我们要维护区间和，那么当我们更新了某一区间的lazy后，我们就必须要用这个lazy标记来维护好区间和

void pushup(ll rt)//用更新后的子节点sum值更新自己的sum值
{
    sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
void pushdown(ll rt,ll len)//将节点rt的lazy标记向其子节点传递，更新子节点sum值
{
    if(!lazy[rt])return;
    lazy[rt<<1]+=lazy[rt];
    lazy[rt<<1|1]+=lazy[rt];
    sum[rt<<1]+=lazy[rt]*(len-((len)>>1));
    sum[rt<<1|1]+=lazy[rt]*(len>>1);
    lazy[rt]=0;
}
void add(ll l,ll r,ll nl,ll nr,ll rt,ll num)
{
    if(l<=nl&&nr<=r)
    {
        lazy[rt]+=num;
        sum[rt]+=(nr-nl+1)*num;
        return;
    }
    pushdown(rt,nr-nl+1);
    int m=(nl+nr)>>1;
    //若操作的区间不能够被某一个点完全覆盖，就将这个区间拆分成几个可以被某几个点所代表区间完全覆盖的区间
    if(m<r)add(l,r,m+1,nr,rt<<1|1,num);
    if(m>=l)add(l,r,nl,m,rt<<1,num);
    pushup(rt);
}

区间查询

当需要对区间[l,r]进行查询时，线段树的思维同样是将区间划分为几个子区间求解，而求子区间的解又是一个子问题，边界是到达[l,r]的子区间
需要注意的是，由于上文维护lazy标记时，我们只将标记停留在了某个区间并未下传（当标记到达一个可以被完全覆盖的区间时便不再下传），于是当查询时，我们每经过一个点就要检查一下此点代表的区间的lazy标记是否被下传，如果没有，就将其下传

void pushup(ll rt)//用更新后的子节点sum值更新自己的sum值
{
    sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
void pushdown(ll rt,ll len)//将节点rt的lazy标记向其子节点传递，更新子节点sum值
{
    if(!lazy[rt])return;
    lazy[rt<<1]+=lazy[rt];
    lazy[rt<<1|1]+=lazy[rt];
    sum[rt<<1]+=lazy[rt]*(len-((len)>>1));
    sum[rt<<1|1]+=lazy[rt]*(len>>1);
    lazy[rt]=0;
}
ll query(ll l,ll r,ll nl,ll nr,ll rt)
{
    if(l<=nl&&nr<=r)//边界，到达[l,r]的子区间
    {
        return sum[rt];
    }
    pushdown(rt,nr-nl+1);
    ll m=(nl+nr)>>1;
    ll ans=0;
    if(m<r)ans+=query(l,r,m+1,nr,rt<<1|1);//二分，相同子问题
    if(l<=m)ans+=query(l,r,nl,m,rt<<1);
    return ans;
}

这里我们可以大致总结出一些规律，即当某一操作（查询或修改）经过某一点时，就应该使用pushdown来下方lazy标记，而当修改时，为了维护非叶节点的标记值，应该用pushup更新节点值

例题 luogu3372
经典操作
code:

#include
using namespace std;
#define loop(i,start,end) for(int i=start;i<=end;i++)
#define ll long long
const int maxn=1000000+10;
ll data[maxn],sum[maxn<<2],lazy[maxn<<2];
int n,q;
void pushup(ll rt)
{
    sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
void pushdown(ll rt,ll len)
{
    if(!lazy[rt])return;
    lazy[rt<<1]+=lazy[rt];
    lazy[rt<<1|1]+=lazy[rt];
    sum[rt<<1]+=lazy[rt]*(len-((len)>>1));
    sum[rt<<1|1]+=lazy[rt]*(len>>1);
    lazy[rt]=0;
}
void buildtree(ll l,ll r,ll rt)
{
    lazy[rt]=0;
    if(l==r)
    {
        sum[rt]=data[l];
        return;
    }
    int m=(l+r)>>1;
    buildtree(l,m,rt<<1);
    buildtree(m+1,r,rt<<1|1);
    pushup(rt);
}
void add(ll l,ll r,ll nl,ll nr,ll rt,ll num)
{
    if(l<=nl&&nr<=r)
    {
        lazy[rt]+=num;
        sum[rt]+=(nr-nl+1)*num;
        return;
    }
    pushdown(rt,nr-nl+1);
    int m=(nl+nr)>>1;
    if(m<r)add(l,r,m+1,nr,rt<<1|1,num);
    if(m>=l)add(l,r,nl,m,rt<<1,num);
    pushup(rt);
}
ll query(ll l,ll r,ll nl,ll nr,ll rt)
{
    if(l<=nl&&nr<=r)
    {
       return sum[rt];
    }
    pushdown(rt,nr-nl+1);
    ll m=(nl+nr)>>1;
    ll ans=0;
    if(m<r)ans+=query(l,r,m+1,nr,rt<<1|1);
    if(l<=m)ans+=query(l,r,nl,m,rt<<1);
    return ans;
}
int main()
{
    //freopen("datain.txt","r",stdin);
    scanf("%d%d",&n,&q);
    loop(i,1,n)scanf("%lld",&data[i]);
    buildtree(1,n,1);
    loop(i,1,q)
    {
        int op;
        scanf("%d",&op);
        if(op==1)
        {
            ll l,r,x;
            scanf("%lld%lld%lld",&l,&r,&x);
            add(l,r,1,n,1,x);
        }
        else if(op==2)
        {
            ll a,b;scanf("%lld%lld",&a,&b);
            printf("%lld\n",query(a,b,1,n,1));
        }
    }
    return 0;
}

例题2
noip 2012 Day2 T2

线段树标记永久化

原理此处不再赘述，代码：

#include
using namespace std;
#define loop(i,start,end) for(register int i=start;i<=end;++i)
#define clean(arry,num) memset(arry,num,sizeof(arry))
#define ll long long
int n,m;
const int maxn=100000+10;
const int maxm=100000+10;
int a[maxn];
ll sum[maxn<<2],tag[maxn<<2];
void buildtree(int l,int r,int rt){
    if(l==r){
        sum[rt]=a[l];
        return;
    }
    int mid=(l+r)>>1;
    buildtree(l,mid,rt<<1);
    buildtree(mid+1,r,rt<<1|1);
    sum[rt]=sum[rt<<1|1]+sum[rt<<1];
}
void update(int l,int r,int nl,int nr,int rt,ll w){
    sum[rt]+=(w*(r-l+1));//区间恒大于等于[l,r] 
    if(l==nl&&nr==r){
        tag[rt]+=w;
        return;
    }
    int mid=(nl+nr)>>1;
    if(r<=mid)update(l,r,nl,mid,rt<<1,w);
    else if(mid<l)update(l,r,mid+1,nr,rt<<1|1,w);
    else update(l,mid,nl,mid,rt<<1,w),
         update(mid+1,r,mid+1,nr,rt<<1|1,w);
}
ll query(int l,int r,int nl,int nr,int rt,ll lazy){
    if(l==nl&&nr==r){
        return sum[rt]+lazy*(nr-nl+1);
    }
    int mid=(nl+nr)>>1;
    if(r<=mid)
        return query(l,r,nl,mid,rt<<1,lazy+tag[rt]);
    else if(l>mid)
        return query(l,r,mid+1,nr,rt<<1|1,lazy+tag[rt]);
    else 
        return query(l,mid,nl,mid,rt<<1,lazy+tag[rt])+
               query(mid+1,r,mid+1,nr,rt<<1|1,lazy+tag[rt]);
}
int main(){
    #ifndef ONLINE_JUDGE
    freopen("datain.txt","r",stdin);
    #endif
    scanf("%d%d",&n,&m);
    loop(i,1,n){
        scanf("%d",&a[i]);
    }
    buildtree(1,n,1);
    
    int op=0;
    loop(i,1,m){
        scanf("%d",&op);
        if(op==1){
            int x,y,k;
            scanf("%d%d%d",&x,&y,&k);
            update(x,y,1,n,1,(ll)k);
        }
        else if(op==2){
            int x,y;
            scanf("%d%d",&x,&y);
            printf("%lld\n",query(x,y,1,n,1,0));
        }
    }
    
    return 0;
}