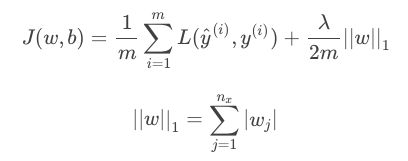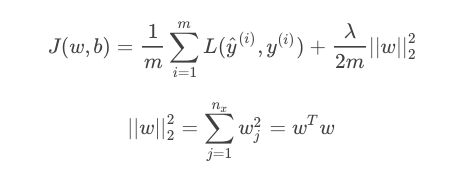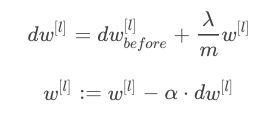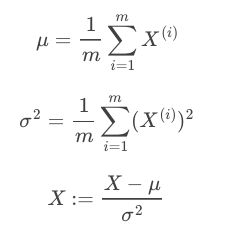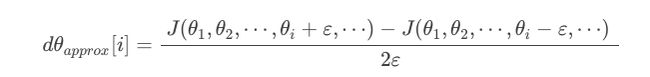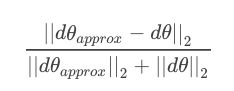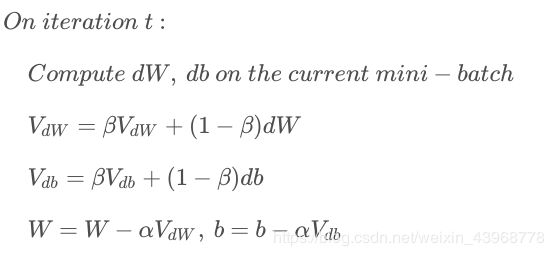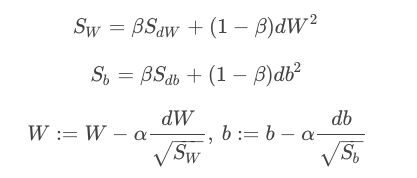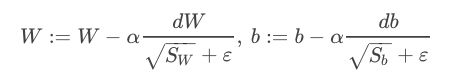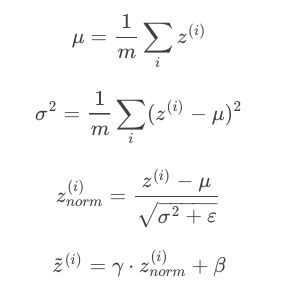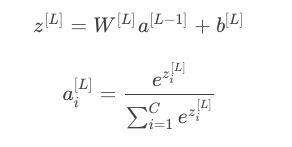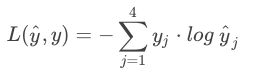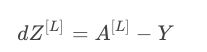吴恩达Course 2 改善深层神经网络 笔记

本文主要参考红色石头Will大佬的完结篇 | 吴恩达deeplearning.ai专项课程精炼笔记全部汇总、何宽大大的【目录】【中文】【deplearning.ai】【吴恩达课后作业目录】，诸多语句和代码摘取其中原句。两位前辈将吴恩达的学习视频和课后编程作业解读得通俗透彻，适合如我这样的初学者，吹爆！
该笔记是吴恩达深度学习课程中Course 2 改善深层神经网络 的全部内容小结，综合了课后编程的部分代码实现和个人思绪归类。

实用层面

Train/Dev/Test sets

数据集分类

• 训练集Training sets用来训练你的算法模型
• 验证集Dev sets用来验证不同算法的表现情况，从中选择最好的算法模型
• 测试集Test sets用来测试最好算法的实际表现，作为该算法的无偏估计。

数据集比例

• 样本数量不大
  • Train : Test = 7 : 3
  • Train : Dev : Test = 3 : 1 : 1
• 样本数量大
  • Train : Test = 99 : 1
  • Train : Dev : Test = 98 : 1 : 1

根据实际样本数量考虑，样本数据量越大，对应的Dev/Test sets比例可以相较Train设置得越低。

数据集注意

• 尽量保证Dev sets和Test sets来自于同一分布
• 对Train sets做如翻转、随机噪声等处理，扩大训练样本数量。
• 不进行无偏估计也可以，即没有Test sets也没有问题。

Bias/Variance

解决高偏差和高方差的方法不同，分别通过训练集和验证集判断是否出现高偏差或高方差，再分别针对性解决。

偏差

偏差过高，即欠拟合。

减少偏差的方法：

• 增加神经网络的隐藏层个数、神经元个数
• 延长训练时间
• 选择其他的神经网络模型

方差

方差过高，即过拟合

减少方差的方法：

• 增加训练样本数据
• 进行正则化
• 选择其他的神经网络模型

Regularization

L2正则化

• L1正则化

• L2正则化
  

L1正则得到的w更加稀疏，能节约存储空间，但微分求导方面更复杂，所以一般用L2正则。

使用L2正则后，梯度下降算法中：

故L2正则也被称作权重衰减，w在迭代中相较于没有正则项的w不断减小。

Dropout正则化

在深度学习网络的训练过程中，对于每层的神经元，按照一定的概率将其暂时从网络中丢弃。

dl = np.random.rand(al.shape[0], al.shape[1]) < keep_prob  # 生成dropout vector
al = np.multiply(al,dl)  # 对l层进行dropout处理，随机删减神经元
al /= keep_prob  # 对l层进行scale up处理，保持期望值不变

在用dropout训练结束后，在测试和实际应用中不需要进行dropout正则化。

其他正则化方法

• 数据扩张（data augmentation），对已有图片进行翻转、缩放或扩大、扭曲、增加噪音等等。
• 提前停止法（early stopping），在避免欠拟合后及时停止训练避免过拟合，但会影响损失函数的减小，不常用。

Normalizing inputs

标准化输入即对训练数据集进行归一化操作，将原始数据减去其均值后，再除以其方差，以此提高训练速度。

让所有输入归一化同样的尺度上，避免其中某些与其他输出差异大的输出发生振荡，方便进行梯度下降算法时能够更快更准确地找到全局最优解。

Vanishing and Exploding gradients

梯度消失和梯度爆炸，是指当训练一个层数非常多的神经网络时，计算得到的梯度可能非常小或非常大，甚至是指数级别的减小或增大，从而让训练过程变得非常困难。

本质原因是权重W随着层数的增加，出现指数型增大或减小，从而影响预测输出。

解决方法即初始化权重W，使得W与n有关，且n越大，W应该越小。

w[l] = np.random.randn(n[l], n[l-1]) * np.sqrt(1 / n[l - 1])  # 激活函数是tanh常用
w[l] = np.random.randn(n[l], n[l-1]) * np.sqrt(2 / n[l - 1])   # 激活函数是ReLU常用

Gradient checking

一维线性

根据求导的定义计算每个$\theta$的近似梯度，利用欧式距离与反向传播得到的$\theta$比较，检查是否一致。

def gradient_check(x,theta,epsilon=1e-7):
    """

    实现图中的反向传播。

    参数：
        x  - 一个实值输入
        theta  - 参数，也是一个实数
        epsilon  - 计算输入的微小偏移以计算近似梯度

    返回：
        近似梯度和后向传播梯度之间的差异
    """

    #使用公式（3）的左侧计算gradapprox。
    thetaplus = theta + epsilon                               # Step 1
    thetaminus = theta - epsilon                              # Step 2
    J_plus = forward_propagation(x, thetaplus)                # Step 3
    J_minus = forward_propagation(x, thetaminus)              # Step 4
    gradapprox = (J_plus - J_minus) / (2 * epsilon)           # Step 5


    #检查gradapprox是否足够接近backward_propagation（）的输出
    grad = backward_propagation(x, theta)

    numerator = np.linalg.norm(grad - gradapprox)                      # Step 1'
    denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)    # Step 2'
    difference = numerator / denominator                               # Step 3'

    if difference < 1e-7:
        print("梯度检查：梯度正常!")
    else:
        print("梯度检查：梯度超出阈值!")

    return difference

高维

For i in num_parameters:

• 计算J_plus[i]:

  • 把 ${\theta }^{+}$ 设置为np.copy(parameters_values)
  • 把 ${\theta }^{+}$ 设置为 ${\theta }^{+}+\epsilon$
  • 使用forward_propagation_n(x, y, vector_to_dictionary( θ⁺ ))来计算$J_i^{+}$

• 计算J_minus[i]: 使用相同的方法计算 ${\theta }^{-}$

• 计算$gradapprox[i]=\frac{J_i^{+}-J_i^{-}}{2\epsilon }$

• 计算梯度

• 计算误差:
  $$difference=\frac{\Vert grad-gradapprox{\Vert }_2}{\Vert grad{\Vert }_2+\Vert gradapprox{\Vert }_2}$$

def gradient_check_n(parameters,gradients,X,Y,epsilon=1e-7):
    """
    检查backward_propagation_n是否正确计算forward_propagation_n输出的成本梯度

    参数：
        parameters - 包含参数“W1”，“b1”，“W2”，“b2”，“W3”，“b3”的python字典：
        grad_output_propagation_n的输出包含与参数相关的成本梯度。
        x  - 输入数据点，维度为（输入节点数量，1）
        y  - 标签
        epsilon  - 计算输入的微小偏移以计算近似梯度

    返回：
        difference - 近似梯度和后向传播梯度之间的差异
        
    """
    # 初始化参数
    parameters_values , keys = dictionary_to_vector(parameters)  # keys用不到
    grad = gradients_to_vector(gradients)
    num_parameters = parameters_values.shape[0]
    J_plus = np.zeros((num_parameters,1))
    J_minus = np.zeros((num_parameters,1))
    gradapprox = np.zeros((num_parameters,1))

    # 计算gradapprox
    for i in range(num_parameters):
        # 计算J_plus [i]。输入：“parameters_values，epsilon”
        # 输出=“J_plus [i]”
        thetaplus = np.copy(parameters_values)                                             # Step 1
        thetaplus[i][0] = thetaplus[i][0] + epsilon                                             # Step 2
        J_plus[i], cache = forward_propagation_n(X,Y,vector_to_dictionary(thetaplus))  # Step 3 ，cache用不到

        # 计算J_minus [i]
        # 输入：“parameters_values，epsilon”
        # 输出=“J_minus [i]”。
        thetaminus = np.copy(parameters_values)                                              # Step 1
        thetaminus[i][0] = thetaminus[i][0] - epsilon                                           # Step 2        
        J_minus[i], cache = forward_propagation_n(X,Y,vector_to_dictionary(thetaminus))  # Step 3 ，cache用不到

        # 计算gradapprox[i]
        gradapprox[i] = (J_plus[i] - J_minus[i]) / (2 * epsilon)

    # 通过计算差异比较gradapprox和后向传播梯度。
    numerator = np.linalg.norm(grad - gradapprox)                                     			# Step 1'
    denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)                        # Step 2'
    difference = numerator / denominator                                             			         # Step 3'

    if difference < 1e-7:
        print("梯度检查：梯度正常!")
    else:
        print("梯度检查：梯度超出阈值!")

    return difference


def dictionary_to_vector(parameters):
    """
    Roll all our parameters dictionary into a single vector satisfying our specific required shape.
    """
    keys = []
    count = 0
    for key in ["W1", "b1", "W2", "b2", "W3", "b3"]:

        # flatten parameter
        new_vector = np.reshape(parameters[key], (-1,1))
        keys = keys + [key]*new_vector.shape[0]

        if count == 0:
            theta = new_vector
        else:
            theta = np.concatenate((theta, new_vector), axis=0)
        count = count + 1

    return theta, keys

def vector_to_dictionary(theta):
    """
    Unroll all our parameters dictionary from a single vector satisfying our specific required shape.
    """
    parameters = {}
    parameters["W1"] = theta[:20].reshape((5,4))
    parameters["b1"] = theta[20:25].reshape((5,1))
    parameters["W2"] = theta[25:40].reshape((3,5))
    parameters["b2"] = theta[40:43].reshape((3,1))
    parameters["W3"] = theta[43:46].reshape((1,3))
    parameters["b3"] = theta[46:47].reshape((1,1))

    return parameters

def gradients_to_vector(gradients):
    """
    Roll all our gradients dictionary into a single vector satisfying our specific required shape.
    """

    count = 0
    for key in ["dW1", "db1", "dW2", "db2", "dW3", "db3"]:
        # flatten parameter
        new_vector = np.reshape(gradients[key], (-1,1))

        if count == 0:
            theta = new_vector
        else:
            theta = np.concatenate((theta, new_vector), axis=0)
        count = count + 1

    return theta

梯度检查的注意事项

• 不要在整个训练过程中都进行梯度检查，仅仅作为debug使用。

• 注意不要忽略正则化项，计算近似梯度的时候要包括进去。

• 梯度检查时关闭dropout，检查完毕后再打开dropout。

• 随机初始化时运行梯度检查，经过一些训练后再进行梯度检查（不常用）。

优化算法

Mini-batch gradient descent

• X⁽ⁱ⁾ ：第i个样本

• Z^[l]：神经网络第l层网络的线性输出

• X^{t}, Y^{t}：第t组mini-batch

• 批量梯度下降算法（Batch gradient descent）：对所有m个样本进行训练，一个epoch进行一次梯度下降算法。

• 小批量梯度下降算法（Mini-batch gradient descent）：将m个样本分成T个子集，对每个mini-batch进行训练。一个epoch进行T次梯度下降算法。

• 随机梯度下降算法（Stochastic gradient descent）：每个样本就是一个子集，对每个样本进行训练。一个epoch进行m次梯度下降算法。

• 当样本总数小于2000时，建议使用批量梯度下降，样本很大使用小批量梯度下降。
• mini-batch大小推荐设置为2的幂，如64，128，256，512等，能提高预算速度。

获得mini-batches的代码实现：

def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
    """
  从（X，Y）中创建一个随机的mini-batch列表

参数：
        X - 输入数据，维度为(输入节点数量，样本的数量)
        Y - 对应的是X的标签，【1 | 0】（蓝|红），维度为(1,样本的数量)
        mini_batch_size - 每个mini-batch的样本数量

    返回：
        mini-bacthes - 一个同步列表，维度为（mini_batch_X,mini_batch_Y）
    """
    np.random.seed(seed)
    m = X.shape[1]                  # 训练集样本数量
    mini_batches = []
   

    # 第一步：打乱顺序
    permutation = list(np.random.permutation(m))  # 返回一个长度为m的随机数组，且里面的数是0到m-1
    shuffled_X = X[:, permutation]   #将每一列的数据按permutation的顺序来重新排列。
    shuffled_Y = Y[:, permutation].reshape((Y.shape[0],m))

    # 第二步：分割
    num_complete_minibatches = math.floor(m/mini_batch_size)   # Math.floor() 返回小于或等于一个给定数字的最大整数。
    for k in range(0, num_complete_minibatches):
        mini_batch_X = shuffled_X[:, k * mini_batch_size : k * mini_batch_size + mini_batch_size]
        mini_batch_Y = shuffled_Y[:, k * mini_batch_size : k * mini_batch_size + mini_batch_size]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    # 如果训练集的大小刚好是mini_batch_size的整数倍，那么已处理完
    # 如果训练集的大小不是mini_batch_size的整数倍，那么处理后续
    if m % mini_batch_size != 0:
        mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size : m]
        mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size : m]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    return mini_batches

损失函数等于每个mini-batch的损失函数除以mini-batch size后的全部求和。

Gradient descent with momentum

指数加权平均处理

$$V_t=\beta V_{t-1}+(1-\beta ){\theta }_t$$

$\beta$决定了指数加权平均的天数，即$\frac{1}{1-\beta }$表示前$\frac{1}{1-\beta }$天进行指数加权平均。

$\beta$值越大，则指数加权平均的天数越多，受前几天的影响越小，平均后的趋势线就越平缓。

由于开始时$V_0$=0，所以初始值会相对小一些，直到后面受前面的影响逐渐变小才趋于正常，解决这个问题需要进行偏移校正（bias correction）：
$$\frac{V_t}{1-{\beta }^t}$$
或者可以忽略初始迭代过程，无需偏移校正。

动量梯度下降算法

从动量的角度，以权重W为例，$V_{dW}$可以看成速度V，dW可以看成是加速度a。指数加权平均实际上是计算当前的速度，当前速度由之前的速度和现在的加速度共同影响。而β<1，又能限制速度$V_{dW}$过大。也就是说，当前的速度是渐变的，而不是瞬变的，是动量的过程。这保证了梯度下降的平稳性和准确性，减少振荡，较快地达到最小值处。

def update_parameters_with_momentun(parameters,grads,v,beta,learning_rate):
    """
    参数：
        parameters - 一个包含参数值的变量
        grads - 一个包含梯度值的字典变量
        v - 包含当前速度的字典变量
        beta - 超参数，动量，实数
        learning_rate - 学习率，实数
    返回：
        parameters - 更新后的参数字典
        v - 包含了更新后的速度变量
    """
    L = len(parameters) // 2 
    for l in range(L):
        # 计算速度
        v["dW" + str(l + 1)] = beta * v["dW" + str(l + 1)] + (1 - beta) * grads["dW" + str(l + 1)]
        v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] + (1 - beta) * grads["db" + str(l + 1)]

        # 更新参数
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * v["dW" + str(l + 1)]
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * v["db" + str(l + 1)]

    return parameters,v

RMSprop

根据变化量dW和d计算$S_w$和$S_b$，来加快振荡小、变化慢的方向的速度，减慢振荡大、变化快的方向的速度，从而达到哪个方向大，就减小该方向的更新速度，从而减小振荡。

为了避免RMSprop算法中分母为零，通常在分母增加一个极小的常数$\epsilon$：

其中，$\epsilon =10^{-8}$，或者其它较小值。

Adam optimization algorithm

Adam（Adaptive Moment Estimation）算法结合了动量梯度下降算法和RMSprop算法。

Adam算法包含了几个超参数，分别是：$\alpha$，${\beta }_1$，${\beta }_2$，$\epsilon$。其中，${\beta }_1$通常设置为0.9，${\beta }_2$通常设置为0.999，$\epsilon$通常设置为$10^{-8}$。一般只需要对${\beta }_1$，${\beta }_2$进行调试。

def update_parameters_with_adam(parameters,grads,v,s,t,learning_rate=0.01,beta1=0.9,beta2=0.999,epsilon=1e-8):
    """
    使用Adam更新参数

    参数：
        parameters - 包含了参数的字典
        grads - 包含了梯度值的字典
        v - Adam的变量，第一个梯度的移动平均值，是一个字典类型的变量
        s - Adam的变量，平方梯度的移动平均值，是一个字典类型的变量
        t - 当前迭代的次数
        learning_rate - 学习率
        beta1 - 动量，超参数，用于第一阶段，使得曲线的Y值不从0开始
        beta2 - RMSprop的一个参数，超参数
        epsilon - 防止除零操作（分母为0）

    返回：
        parameters - 更新后的参数
        v - 第一个梯度的移动平均值，是一个字典类型的变量
        s - 平方梯度的移动平均值，是一个字典类型的变量
    """
    L = len(parameters) // 2
    v_corrected = {}  # 偏差修正后的值
    s_corrected = {}  # 偏差修正后的值

    for l in range(L):
        # 梯度的移动平均值，输入："v , grads , beta1"，输出：" v "
        v["dW" + str(l + 1)] = beta1 * v["dW" + str(l + 1)] + (1 - beta1) * grads["dW" + str(l + 1)]
        v["db" + str(l + 1)] = beta1 * v["db" + str(l + 1)] + (1 - beta1) * grads["db" + str(l + 1)]

        # 计算第一阶段的偏差修正后的估计值，输入"v , beta1 , t" , 输出："v_corrected"
        v_corrected["dW" + str(l + 1)] = v["dW" + str(l + 1)] / (1 - np.power(beta1,t))
        v_corrected["db" + str(l + 1)] = v["db" + str(l + 1)] / (1 - np.power(beta1,t))

        #计算平方梯度的移动平均值，输入："s, grads , beta2"，输出："s"
        s["dW" + str(l + 1)] = beta2 * s["dW" + str(l + 1)] + (1 - beta2) * np.square(grads["dW" + str(l + 1)])
        s["db" + str(l + 1)] = beta2 * s["db" + str(l + 1)] + (1 - beta2) * np.square(grads["db" + str(l + 1)])

        #计算第二阶段的偏差修正后的估计值，输入："s , beta2 , t"，输出："s_corrected"
        s_corrected["dW" + str(l + 1)] = s["dW" + str(l + 1)] / (1 - np.power(beta2,t))
        s_corrected["db" + str(l + 1)] = s["db" + str(l + 1)] / (1 - np.power(beta2,t))

        #更新参数，输入: "parameters, learning_rate, v_corrected, s_corrected, epsilon". 输出: "parameters".
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * (v_corrected["dW" + str(l + 1)] / np.sqrt(s_corrected["dW" + str(l + 1)] + epsilon))
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * (v_corrected["db" + str(l + 1)] / np.sqrt(s_corrected["db" + str(l + 1)] + epsilon))

    return (parameters, v, s)

Learning rate decay

通过不断减小学习因子，减小步进长度，来减小梯度振荡。
$$\alpha =\frac{1}{1+decayRate\ast m}{\alpha }_0$$
decayRate是可调的参数，m是当前样本的个数。

也有其它可供选用的计算公式。

The problem of local optima

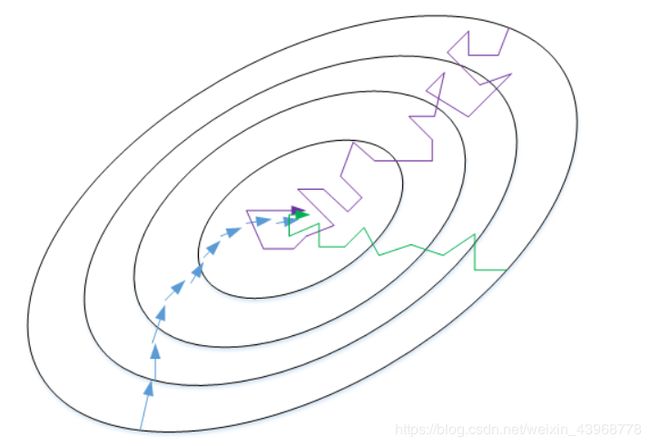
鞍点是在某些方向上看是极小值，某些方向看是极大值的点，mini-batch可以很好避免鞍点。

停滞期是梯度接近于零的平缓区域。

• 只要选择合理的强大的神经网络，一般不太可能陷入局部最优解。
• 停滞期可能会使梯度下降变慢，降低学习速度。

超参数调试、Batch正则化和编程框架

Tuning Process

超参数

( 重要性从高到低，排名不绝对 )

• $\alpha$ ：学习因子
• $\beta$：动量梯度下降因子
• hidden units：各隐藏层神经元个数
• mini-batch size：批量训练样本包含的样本个数
• layers：神经网络层数
• learning rate decay：学习因子下降参数
• ${\beta }_1$，${\beta }_2$，$\varepsilon $：Adam算法参数（一般设置为0.9，0.999， 10^-8）

超参数调试

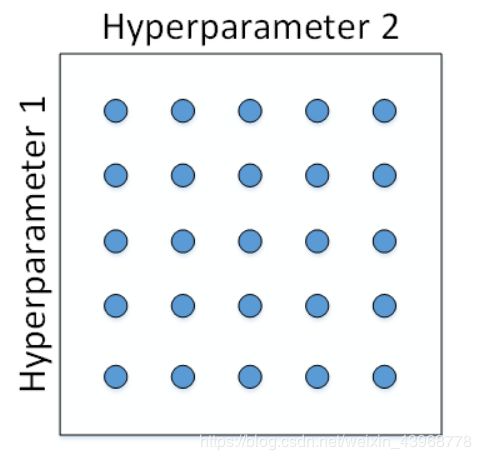
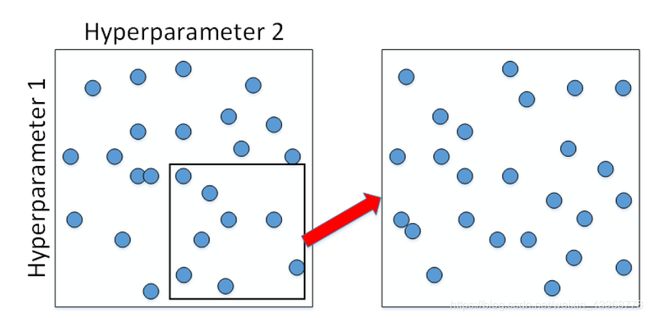
均匀采样

随机采样

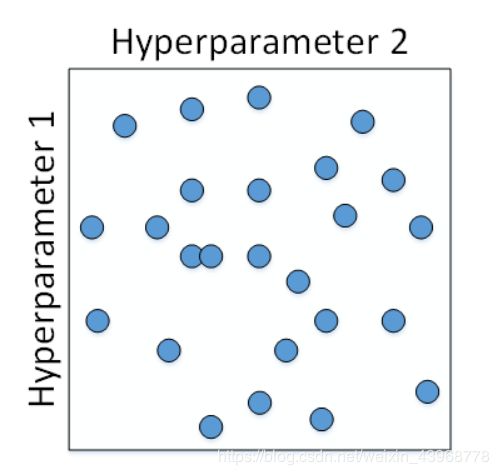
针对表现较好的区域模型，进行由粗到细的采样：

尺度变化采样

例如对于超参数$\alpha$最佳的调整范围相较于其他超参数非常小，此时将linear scale转换成log scale：

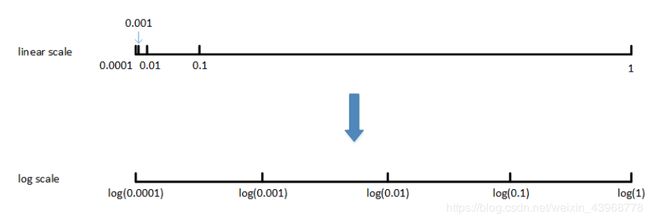
对应代码实现：

m = np.log10(a)
n = np.log10(b)
r = np.random.rand()
r = m + (n-m)*r
r = np.power(10,r)

如果例如动量梯度因子$\beta$取值范围在[0.9，0.999]之间，只需对$1-\beta$在[0.001，0.1]区间进行log变换即可。

同时需要注意，对$\beta$接近1的区间，应该采集得更密集一些，因为例如在[0.9000，0.9005]区间，$\frac{1}{1-\beta }$几乎没有变化。

训练模式

• Babysitting one model：一次只对一个模型进行训练，调试不同的超参数，寻找最佳表现。
• Training many models in parallel：对多个模型同事训练，每个模型上调试不同的超参数，选择最佳模型。

Normalizing activations in a network

Batch Normalization

训练过程中的实现

对训练数据集进行归一化操作，这种标准化输入只是对输入进行了处理，对于隐藏层的标准化处理就是Batch Normalization。

Batch Normalization能减小协变量移位的影响，后面层数的W对前面的W包容性更强，减少各层W和b的耦合性，模型更加健壮，鲁棒性更强。也能起到轻微的正则化效果。

一般对$Z^{[l-1]}$进行处理，而不是$A_{[l-1]}$，其实差别不大。

$\gamma$和$\beta$是learnable parameters，可以通过梯度下降等算法求得，作用是让${\bar{z}}^{(i)}$的均值和方差为任意值，避免所有的${\bar{z}}^{(i)}$均值都为0，方差都为1。如果各隐藏层的输入均值在靠近0的区域即处于激活函数的线性区域，不利于训练好非线性神经网络。

因为Batch Norm对各隐藏层$Z^{[l]}=W^{[l]}{A}^{[l-1]}+b^{[l]}$有去均值的操作，所以这里的常数项$b^{[l]}$可以消去，其数值效果完全可以由${\bar{Z}}^{[l]}$中的$\beta$来实现。因此，我们在使用Batch Norm的时候，可以忽略各隐藏层的常数项$b^{[l]}$。在使用梯度下降算法时，分别对$W^{[l]}$，${\beta }^{[l]}$和${\gamma }^{[l]}$进行迭代更新。

测试过程中的实现

在测试过程中，如果只有一个样本，求其均值和方差没有意义，需要采用指数加权平均的方法对均值和方差进行估计：

对于第$l$层隐藏层，考虑所有mini-batch在该隐藏层下的${\mu }^{[l]}$和${\sigma }^{2[l]}$，然后用指数加权平均的方式来预测得到当前单个样本的的${\mu }^{[l]}$和${\sigma }^{2[l]}$。这样就实现了对测试过程单个样本的均值和方差估计。最后，再利用训练过程得到的${\beta }^{[l]}$和${\gamma }^{[l]}$值计算出各层的${\bar{z}}^{(i)}$值。

Training a softmax classifier

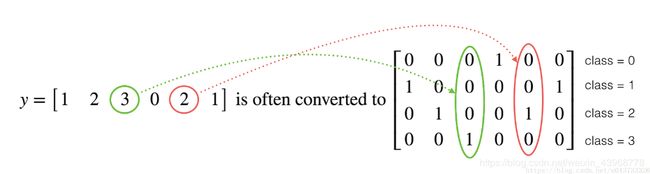
独热编码

很多时候在深度学习中y向量的维度是从0到C−1，C是指分类的类别数量，如果C=4，那么需要使用独热编码（”one hot” encoding）转换y：

代码实现：

• 利用numpy快速实现

Y = np.eye(C)[Y.reshape(-1)].T

np.eye(C)是构造一个对角线为1的对角矩阵， Y.reshape(-1)把Y压缩成向量，np.eye(C)[Y.reshape(-1)]的意思是取对角矩阵的相应行， 最后.T做转置

• 或用其他深度学习框架的语句实现。

softmax分类器

例如对于C=4的多元分类问题，称为softmax回归模型。

其激活层的函数为：

其softmax分类器的损失函数为：

对于m个样本的代价函数为：

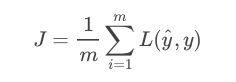
其反向传播过程中导数推导出来为：

Deep learning frameworks

Caffe/Caffe2，CNTK，DL4J，Keras，Lasagne，mxnet，PaddlePaddle，TensorFlow，Theano，Torch等都是深度学习的框架。

一般选择框架的准则：易于编程、速度快、完全开源。

Tensorflow

TensorFlow的最大优点就是采用数据流图（data flow graphs）来进行数值运算。图中的节点（Nodes）表示数学操作，图中的线（edges）则表示在节点间相互联系的多维数据数组，即张量（tensor）。而且它灵活的架构让你可以在多种平台上展开计算，例如台式计算机中的一个或多个CPU（或GPU），服务器，移动设备等等。

tensorflow实现代码结构

1. 创建Tensorflow变量（此时，尚未直接计算）
2. 实现Tensorflow变量之间的操作定义
3. 初始化Tensorflow变量
4. 创建Session
5. 运行Session