论文《Continuous 3D Label Stereo Matching using Local Expansion Moves》学习

Abstract

（2018 SCI一区）提出了一种基于图割的局部展开运动的精确立体匹配方法。这种新的运动生成方法被用来有效地在一对马尔可夫随机场(MRF)上推断每个像素的三维平面标签，该随机场有效地结合了最近提出的斜斑匹配和曲率正则化项。对于小网格区域，局部展开运动表现为定义的多个α-展开。局部扩张运动通过两种方式扩展了传统的扩张运动：局部化和空间传播。通过定位，我们根据局部α展开的位置使用不同的候选α-标签。通过空间传播，我们设计了局部α-展开来传播当前为邻近区域分配的标签。通过这种定位和空间传播，我们的方法可以有效地利用随机搜索推断具有连续标签空间的MRF模型。与以往基于融合移动或信念传播的方法相比，我们的方法有几个优点；它产生子模块移动，从而得到子问题的最优性；它有助于找到好的、平滑的、分段的线性视差图；它适合于并行化；它可以使用代价-体积法。加速匹配成本计算的滤波技术。即使使用简单的成对MRF，我们的方法在Middlebury立体声基准v2和v3中也有最好的性能。
关键词： 立体视觉，三维重建，图形切割，马尔可夫随机域，离散-连续优化。

1. Introduction

立体视觉常常会因为匹配成本、平滑度正则化甚至推理等原因而产生对重建前向平行曲面的偏好[5]、[45]。

基于分段的立体[4]算法通过视差平面分段表示视差图，可以有效地消除重覆盖曲面的偏置问题，但重覆盖曲面的约束条件是分段平面。近年来，在克服基于分段的立体视觉限制的同时，独立实现了两个突破。

其中一个突破是使用倾斜patch匹配[5]的匹配成本。该方法利用局部视差平面对每个像素点$p$的视差$d_p$进行过参数化

定义在图像域$（u，v）$上，对每个像素$p$估计三元组$（a_p，b_p，c_p）$，而不是直接估计$d_p$。然后将匹配窗口倾斜，使之符合式(1)，从而在窗口内产生线性变化的差异，从而即使使用较大的匹配窗口，也能准确地测量patch的不相似性。

另一个关键发明是通过切平面标签进行曲率正则化[27]，[33]。与形成高阶项的二阶光滑度[45]不同，这种曲率正则化由传统的（fronto-parallel）线性[19]和截断的线性模型等成对项很好地表示，并且可以处理平面以外的光滑曲面。

给定斜片匹配[5]和基于切线的曲率正则化[33]，使用3d平面标签允许我们使用不受fronto平行偏移的成对马尔可夫随机场（MRF）[12]建立新的立体模型。然而,尽管立体声与标准1D离散差异标签[8],[23],[42]等离散优化器可以直接解决图削减(GC)[7],[24]和信仰传播(BP)[11],[47],这样的方法不能直接用于连续3D标签由于巨大或无限标签空间$(a,b,c)\in \mathbb{R}$。

为了有效地推断3d标签，最近成功的方法[3]、[5]、[14]、[32]使用PatchMatch[1]、[2]，这是一种使用空间标签传播的推断算法。在PatchMatch中，每个像素都是按照栅格扫描顺序更新的，它的细化标签作为候选标签传播到下一个像素。进一步在[3]中，这种顺序算法与BP相结合，产生了一个有效的成对MRFs优化器PMBP。相反，GC通过考虑变量间的交互作用同时改进所有变量，并且这个全局属性有助于优化避免坏的局部最小值[38]，[45]。为了充分利用这一点，并通过GC有效地推断三维平面，利用空间传播是非常重要的。然而，将这种空间传播合并到基于GC的优化中并非易事，因为使用GC的推理是同时处理所有节点的，而不是像Patchmatch和BP那样一个接一个地依次处理。

在本文中，我们介绍了一种新的移动生成方案——局部扩展移动，它使GC优化中的空间传播成为可能。局部的扩张举措提出了尽可能多的α扩张[8]定义为一个小范围的区域在不同的位置。每一个小的或局部的α展开都试图用GC以能量最小化的方式改善其局部区域的当前标签。在这里，允许这些当前标签移动到候选标签α，该候选标签α对每个局部α展开唯一给定，以实现有效的标签搜索。与此同时，此过程的目的是为附近像素在局部区域传播当前标签。对于经常显示局部平面结构的自然场景，联合使用局部展开移动和GC有一个有用的特性。它允许在一个局部区域内的多个像素通过一个最小截距被分配到相同的视差平面，以找到一个平滑的解决方案。能够同时更新多个变量也有助于避免陷入糟糕的局部最小值。

对于连续MRF推理，通常使用基于融合的方法(使用GC[25])和一些启发式方法来生成视差图提案[33]、[34]、[45]。我们的工作在patchmatch和gc两种明显不同的推理方法之间建立了桥梁，并且可以利用patchmatch和基于融合的方法中使用的启发式方法，从而提高效率和准确性。

我们的方法的优点如下。1）我们的局部展开移动方法产生子模移动，保证在每一个最小割（子问题最优）处的最优标记，而在一般的融合移动中则不保证这一点[25]。2)这种最优性和空间传播允许随机搜索，而不是像融合方法[25]、[45]那样使用外部方法生成可信的初始建议，这可能会限制可能的解决方案。3）由于气相色谱和局部展开的良好性质，我们的方法比BP[3]更准确。4)与其他基于PatchMatch的[3]、[5]、[14]方法不同，我们的方法可以结合[32]的快速成本滤波技术。这样，我们可以有效地降低一元项的计算复杂度$o(W)$到大约$o(1)$，从支持窗口大小中移除依赖项$|W|$。5)与PMBP[3]不同，我们的方法非常适合CPU和GPU并行化。与多个CPU核心,每个地方α-expansions (min-cut计算)可以单独并行执行。使用GPU实现，可以更有效地并行执行一元项的计算，以进一步加速。

这篇论文是我们会议论文[39]的扩展版本。扩展总结如下。我们在3.1节中对我们的方法对分段平面场景的优先性进行了理论验证，在3.3节中对我们算法的子问题最优性进行了理论验证。通过两种方法提高了算法的效率;在第3.3节中，我们展示了局部展开移动算法的并行性;在第3.5节中，我们证明了[32]的快速成本滤波技术可以用于我们的方法。实验中对这两种扩展的有效性进行了彻底的评估，并且我们证明，即使是一个cpu实现，该方法的运行时间也比我们以前的gpu实现快2.1x左右[39]，具有可比的甚至更高的精度。最后，我们在sec中添加了实验评估。4表明我们的方法优于基于融合的方法[33]和在最新的Middlebury基准V3中注册的所有最新方法。我们的代码在网上公开（https://github.com/t-taniai/localexpstereo）。

2. Related work

2.1 MRF stereo methods

MRF立体方法可分为离散立体法、分段立体法和连续立体法。

离散立体[8]、[23]、[42]将立体匹配定义为一个离散的多标记问题，其中每个像素分别分配一个预定义的离散视差值。针对这一问题，可以直接使用BP[11]、[47]、TRW[21]、GC[7]、[24]等多种功能强大的离散优化器。成功的结果显示使用GC和扩展移动[8]，[38]。在展开运动中，将多标号问题归结为一系列二元标号问题，如果只有成对势$\psi$满足以下展开运动的子模性[8]，[22]，每一个都可以用GC精确求解：

基于分段的立体[4]、[15]、[41]、[43]为每个过分段的图像区域指定3d视差平面。尽管这种方法产生连续值差异，但它严格地限制了重建为分段平面表示，并受到初始分割质量的影响。较新的方法通过使用复杂的分层mrf[6]、多尺度分割[26]或联合估计分割[46]来减轻这些限制。

最后一组，我们的方法属于连续立体[3]，[5]，[14]，[32]，[33]，[45]，其中每个像素分配一个不同的连续视差值。一些方法[33]，[45]使用融合移动[25]，这是一种操作，结合两个解决方案，使一个更好的一个(二进制融合)通过解决一个非子模块二进制标记问题使用QPBO-GC[22]。在这种方法中，首先由其他外部方法（例如，基于段的立体图[45]）生成多个连续值视差图（或文献[25]中的所谓建议），然后将这些方法组合为二进制融合序列。我们的方法与这种基于融合的方法的不同之处在于，我们在推理过程中使用空间传播和随机化搜索，我们只需要一个随机化的初始解，而不需要外部方法生成的初始解。此外，我们的方法中提出的二进制能量总是子模块的，允许通过GC(子问题优化)进行精确推理。更重要的是，我们提供了一个有效的推理机制，在概念上与方案生成是正交的。因此，在融合方法[33]、[34]、[45]中使用的传统方案生成方案可以被纳入我们的方法中以进行进一步的改进。bleyer等人[5]提出的一种立体方法提出了使用patchmatch[1]，[2]推断的3d视差平面进行精确的光一致性测量。Heise等人[14]使用凸优化将huber正则化合并到[5]中。Besse等人[3]指出Patchmatch与BP的密切关系，提出了一种适用于成对连续mrf的统一方法patchmatch-bp（PMBP）。在精神上，PMBP可能是最接近我们的方法，但是我们使用GC而不是BP来进行推断。因此，我们的方法能够利用GC[38]更好的收敛性来获得更高的精度。此外，我们的方法可以有效地并行计算一元匹配代价，甚至最小割运算。

2.2 Cost-volume filtering

基于块的立体方法通常使用成本-体积过滤来快速实现。通常，计算一个patch的匹配代价C需要$O(|W|)$的计算量，其中$|W|$是patch的大小。然而，给定表示特定视差标签$d$的像素级原始匹配成本$||I(p)-I^{\prime }(p-d)||$的成本-体积切片${\rho }_d(p)$，通过将滤波应用于成本图$C_d(p)={\sum }_q{\omega }_{pq}{\rho }_d(p)$可以有效地计算基于patch的匹配成本。这里，滤波核${\omega }_{pq}$表示$p$处的匹配窗口。如果使用恒定时间滤波，则在$o(1)$中有效地计算每个匹配代价$C_d(p)$。

盒形滤波利用积分图像可以达到$o(1)$，但这种简单的滤波使物体边界变平。对于这个边界问题，Yoon和Kweon[48]提出了一种自适应支持窗口技术，使用联合双边滤波[35]进行成本滤波。这种自适应窗口技术虽然成功地解决了边界问题[16]，但由于双边滤波的复杂性，它涉及到$O(|W|)$的计算。最近，他等人[13]提出了一种恒定时间的边缘感知滤波，称为引导图像滤波。将该滤波方法应用于[17]、[36]的成本-体积滤波方法中，实现了边缘感知和匹配成本计算的$o(1)$。

原则上，使用patchmatch推断的立体方法[3]、[5]、[14]不能利用代价滤波加速，因为在这些方法中，候选视差标签是动态地给定给每个像素的，并且我们不能生成一致的标签代价体积片${\rho }_d(p)$。关于这个问题，Lu等人[32]扩展Patchmatch[5]以使用超级像素作为成本计算单位。在他们称为patchmatch滤波器（PMF）的方法中，[17]、[36]的快速代价体积滤波被应用于小的子区域，并且近似达到了$o(1)$的复杂度。我们将在第3.5节中展示，他们的分区滤波技术可以有效地融入到我们的方法中，并且我们比他们的局部立体方法获得更高的精度[32]。

3. Proposed method

本节描述我们提出的方法。给定两个输入图像$I_L和I_R$，我们的目的是估计这两个图像的视差。

在3.1节中，我们首先讨论模型的几何性质。然后，我们在第3.2节中定义了能量函数，并在第3.3节中描述了优化策略的基本思想及其性质。整个优化过程在第3.4节中给出，我们在第3.5节中进一步讨论了一个快速实现。

3.1 Geometric interpretation to slanted patch matching

式(1)隐式地假设真实的视差图近似分段线性。虽然在[5]中没有讨论，但是线性视差与平面[4]、[33]的运动密切相关。形式上，如果在三维世界坐标$(x,y,z)\in {\mathbb{R}}^3$中存在一个平面

由$(a_p^{\prime },b_p^{\prime },c_p^{\prime },h_p^{\prime })$参数化，由这个几何平面引起的运动用视差平面表示

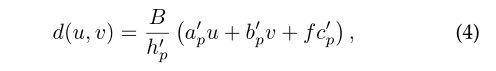
其中$B和f$为立体相机的基线和焦距。这种分段平面假设是合理的，因为许多自然场景近似地呈现局部平面。正如我们稍后将讨论的，这一事实也支持我们的方法设计，因为我们的模型和推理都更倾向于分段线性视差图，同时具有表达任意曲面的能力。

3.2 Formulation

我们利用三维平面标签公式，利用强大的倾斜patch匹配[5]和曲率正则化[33]。这里，每个像素p的视差dp都被一个3D平面$d_p=a_{p}u+b_{p}v+c_p$过度参数化。因此，我们寻找一个映射$f_p=f(p):\Omega \to L$，为左右图像中的每个像素p指定一个视差平面$f_p=(a_p,b_p,c_p)\in L$。根据传统的MRF立体方法[8]、[23]、[33]、[42]，我们基于成对MRF最小化以下能量函数来估计$f$。

第一项称为数据项或一元项，用于测量匹配像素之间的照片一致性。不均匀平面$f_p$定义了从一幅图像中的像素$p$到另一幅图像中的对应点之间的扭曲。第二项称为平滑项或成对项，它惩罚相邻像素对$(p，q)\in N$之间的不连续性。我们在下面定义这些术语。

数据项
为了测量照片的一致性，我们使用了最近由[5]提出的倾斜patch匹配术语。左边图像中$p$的数据项定义为

这里，$W_p$是一个以$p$为中心的正方形窗口。权重${\omega }_{ps}$实现了文[48]中提出的自适应支持窗口。为此，我们将[5]、[48]中使用的双边滤波器权重替换为更高级的引导图像滤波[13]，如下所示。

这里，$I_p=I_L(p)/255$是一个标准化的颜色向量，${\mu }_k和{\sum }_k$是局部回归窗口$W_k^{\prime }中I_p$的均值和协方差矩阵，$e$是一个具有小的正系数以避免过度拟合的恒等式矩阵。我们将在第3.5节中讨论如何有效地计算这种滤波。

给定视差平面$f_p=(a_p，b_p，c_p)$，式（6）中的函数$\rho (s|f_p)$测量窗口$W_p$中的支持像素$s=(s_u，s_v)$与其在右图像中的匹配点之间的像素差异。

as

这里,${\nabla }_{x}I$代表了图像的灰度值梯度$I$的$x$分量,和$\alpha$是一个因素,平衡色彩和梯度项的权重。这两个术语是截断${\tau }_{col}$和${\tau }_{grad}$为闭塞的地区增加鲁棒性。我们对$I_R(s^{\prime })$使用线性插值，而对${\nabla }_x$使用Sobel滤波核[-0.5 0 0.5]。当数据项定义在右图像上时，我们交换等式（7）和（9）中的$I_L和I_R$，并在等式（8）中添加视差值。

平滑项
对于平滑项，我们使用基于曲率的二阶平滑正则化项[33]定义为

这里，${\omega }_{pq}$是一个对比敏感的权重，定义为

$\gamma$是一个用户定义的参数。$ϵ$是一个很小的常数值，它给出了权重${\omega }_{pq}$的一个下界，以提高对图像噪声的鲁棒性。函数${\bar{\psi }}_{pq}(f_p,f_q)$根据视差惩罚$f_p和f_q$之间的不连续性。

其中$d_p(f_p)=a_q{p}_u+b_q{p}_v+c_p$。式(12)中的第一项通过p点处的视差值来度量$f_p和f_q$之间的差值，第二项在$q$点处的定义类似。我们将${\bar{\psi }}_{pq}(f_p,f_q)$视为图2(a)中的红色箭头。${\bar{\psi }}_{pq}(f_p,f_q)$在${\tau }_{dis}$处被截断，以允许深度边缘处视差的急剧跳跃。

注意，当$a=b=0$时，${\bar{\psi }}_{pq}(f_p,f_q)=2|c_p-c_q|$；因此，光滑项${\bar{\psi }}_{pq}(f_p,f_q)$自然地扩展了传统的截断线性模型[8]，尽管后者具有前向平行偏差，应该避免[33]，[45]。同样，如图2 (b)所示，当$f_p=f_q$时，这一项为零。这就强制了分段线性视差映射和分段平面物体表面。此外，为了利用GC，这一项满足以下特性。

引理1 式(10)中的项${\bar{\psi }}_{pq}(f_p,f_q)$满足式(2)中展开运动的子模性。
（证明见[33]和附录A）

3.3 Local expansion moves

在这一部分，我们描述了我们的方法的基本思想，局部扩张移动，作为本文的主要贡献。我们首先简要回顾了原始的扩展移动算法[8]，然后描述了如何扩展它来有效地优化连续MRFs。

展开移动算法[8]是对式(5)中的成对MRFs进行离散优化的一种方法，它迭代地解决了以下一系列二进制标记问题

所有可能的候选标签${}^{\forall }\alpha \in L$。在这里,二进制变量$f_p^{\prime }$为每个像素分配当前标签$f_p^{(t)}$或候选标签$\alpha$。如果$E(f)$中的所有成对项满足式(2)的条件，则式(13)中的二元能量$E(f^{\prime })$是亚模的，因此可以通过GC[8]精确地求解此最小化（子问题最优）。这里，保证能量不增加：$E(f^{(t+1)})\le E(f^{(t)})$。然而，在我们的设置中，标签空间$L$是一个三维连续空间$(a,b,c)$；因此，不能使用这种穷尽的方法。

我们的局部扩张运动通过两种方式扩展了传统的扩张运动：局部化和空间传播。通过定位，我们根据等式（13）中像素$p$的位置使用不同的候选标签$\alpha$，而不是对所有像素使用相同的$\alpha$标签。这是合理的,因为差距应该不同位置的分布位置,因此候选标签$\alpha$的选择应相应地不同。通过空间传播，我们将类似Patchmatch推断[1]、[2]、[5]的标签传播合并到GC优化中，并通过GC将当前分配的标签传播到附近的像素。这种传播背后的假设是，如果一个好的标签被分配给一个像素，那么这个标签很可能也是对附近像素的一个很好的估计。定位和空间支撑一起使我们能够使用一个强大的随机搜索方案，在那里我们不再需要像通常在基于融合的方法[25]中那样生成初始解决方案。下面我们将详细描述我们的算法。

局部α-扩张空间传播
我们首先定义了一个网格结构，将图像域$\Omega$划分为网格区域$C_{ij}\subset \Omega$，这些网格区域由二维整数坐标$(i,j)\in \mathbb{Z}$索引。我们将每个网格区域称为一个单元格。我们在本文中简单地假设规则的正方形单元格，但这可以扩展到使用超像素[18]、[29]、[40]。在高水平上，细胞的大小在定位水平和空间传播范围之间保持平衡。细胞尺寸越小，定位越好，但空间传播范围越短。在稍后的第3.4节中，我们将介绍多种网格结构的不同大小，以很好地平衡这两个因素，但现在让我们集中于使用一种网格结构。

给定一个网格结构，我们在每个单元$(i,j)$定义一个局部$\alpha -$展开，具体表示为${\alpha }_{ij}-$展开。我们进一步定义了每个${\alpha }_{ij}-$展开的两类区域：中心区域$C_{ij}$和展开区域

即3×3个细胞，由中心区$C_{ij}$及其8个相邻细胞组成。

图3的中间部分,我们专注于扩大地区和说明一个${\alpha }_{ij}-$展开是如何工作的。我们首先从中心区域$C_{ij}$中随机选择一个像素$r$，取其当前分配的标签为$(a,b,c)=f_r$。然后，我们通过扰动当前标签${\alpha }_{ij}=(a，b，c)+\Delta$来生成候选标签${\alpha }_{ij}$。最后，我们通过选择像素$p$的当前标签$f_p$或候选标签${\alpha }_{ij}$来更新扩展区域$r_{ij}$中像素$p$的当前标签。这里，与式（13）类似，我们通过用二元变量最小化$E(f^{\prime })$来更新部分标号：对于$p\in R_{ij}有f^{\prime }p\in \{f_p，{\alpha }_{ij}\}$，对于$p\notin R_{ij}，f_p^{\prime }=f_p$。因此，我们得到一个改进的解作为它的最小值或能量更低或相等。

注意，使扩展区域$R_{ij}$大于标签选择区域$C_{ij}$是实现空间传播的关键思想。我们可以看到这一点，因为在无扰动的${\alpha }_{ij}$-展开中（Δ=0），中心区域cij中的当前标签$f_p$可以作为候选标签${\alpha }_{ij}$传播到$R_{i,j}$中其附近的像素。我们迭代使用这个${\alpha }_{ij}$-展开，如算法1所示。类似于Patchmatch算法[1]，这个迭代算法有传播（第1-4行）和细化（第9-14行）步骤。在传播步骤中，我们应用无扰动的${\alpha }_{ij}$-展开从$C_{i,j}$向$R_{i,j}$传播标签。在求精步骤中，我们应用摄动尺寸指数减小的${\alpha }_{ij}$-展开来求精标签。我们当地的扩张方法是概念上正交移到任何这样的启发式生成${\alpha }_{ij}$。作为这样一个例子，我们在第5-8行使用RANSAC 命题器，方法是遵循基于融合的方法中使用的传统生成方案[33]，[45]。这里，我们使用LO-RANSAC [9]将平面拟合到$C_{ij}$区域的当前视差图f，从而生成${\alpha }_{ij}$。我们执行这个迭代αij扩张在每一个细胞$(i,j)$。

这种局部α展开方法具有以下有用的性质。
分段线性： 它有助于获得光滑的解。在每个${\alpha }_{ij}$-展开中，允许展开区域$R_{ij}$中的多个像素以一个二进制能量最小化的方式同时移动到相同的候选标签${\alpha }_{ij}$，这与一次仅更新一个像素的BP形成对比。由于标签在这里代表一个视差平面，我们的方法有助于获得分段线性视差图，从而获得我们在第3.1节中讨论过的分段平面。
成本过滤加速： 利用成本-体积过滤技术，可以加速公式（6）中匹配成本${\varphi }_p(f_p)$的计算。我们在第3.5节中对此进行了详细讨论。
最优性和并行性: 利用我们的能量公式，保证算法1中的每一个二进制能量最小化都可以通过GC得到最优解。此外,我们可以有效地执行许多${\alpha }_{ij}$扩张以类似的方式。我们将在以下几节中讨论这些问题。

互不相交的地方α扩张
上一节介绍了每个局部$\alpha$-展开的行为，在此我们讨论了局部$\alpha$-展开的调度。我们需要一个适当的调度，因为局部$\alpha$-展开由于重叠的展开区域而不能同时执行。有效执行局部$\alpha$扩张,我们把它们分成组,这样局部的$\alpha$扩张每组中是相互分离的。具体地说，我们给每个${\alpha }_{ij}$-展开分配一个群索引$k$，由

在一组和另一组中执行迭代${\alpha }_{ij}$-展开。如图4中所示,这个分组规则选择${\alpha }_{ij}$-展开在每四个垂直和水平细胞在同一组,和它相当于16组相互不相交的地方$\alpha$扩张。在图5中，我们将一组不相交的局部$\alpha$-展开视为橙色区域，并将其视为图3右侧具有三种不同网格结构的单层堆栈。


注意，在每组中，我们在相邻的局部$\alpha$-展开之间留有一个单元宽度的间隙。这些间隙是为了保证局部$\alpha$展开的子模性和独立性。通过子模性，我们可以证明我们的局部α-展开总是产生子模能量，因此可以通过GC得到最优解。由于这种子模块性，我们可以使用标准的GC算法[7]，而不是昂贵的QPBO-GC算法[22]，这在基于融合的方法中通常是必需的。通过独立,我们可以表明,局部$\alpha$-展开在同一组不相互干扰。因此，我们可以并行地同时执行它们。GC算法的并行化是计算机视觉[30]、[37]研究的热点。我们的方案很简单，可以直接使用现有的GC实现。：下一节将给出这种次模量和独立性的证明。

子模块性与独立性
为了正式解决局部α展开的子模块性和独立性，我们使用融合移动的形式来讨论它[25]。假设一个当前解f和一组相互不相交的${\alpha }_{ij}$-展开式被应用。同时应用这些${\alpha }_{ij}$扩张相当于以下聚变能最小化:

如果$p$属于这个群中的任何一个扩张区域$R_{ij}$，则建议解g被设置为$g_p={\alpha }_{ij}$；否则，$p$处于间隙中，因此我们将${\varphi }_p(g_p)$赋给一个用于强制$f_p^{\prime }=f_p$的无限一元代价。在图3的右侧，这个提议的视差图g被可视化为单层堆栈。我们证明了以下引理:

引理2: 子模性:式(16)中的二元能量为子模，即式(16)中所有的成对交互作用都满足融合移动[22]、[25]的子模块性:


引理3: 独立性:如果$p和q$在不同的展开区域，分配给$f_p^{\prime }和f_q^{\prime }$的值不会相互影响。

证明:当且仅当存在连接$p=s_0和q=s_n$的有效成对交互链$C=\{\psi (f_{s_0}^{\prime },f_{s_1}^{\prime }),...,\psi (f_{s_{n-1}}^{\prime },f_{s_n}^{\prime })\}$时，fp和fq具有交互。但是没有这样的链，因为c不可避免地在一个间隙处包含常数项或一元项（图5中的${\psi }_{cd}和{\psi }_{ac}$）。

3.4 Optimization procedure

使用上一节所示的局部展开移动，我们在本节中给出了整体优化过程，并在算法2中进行了总结。

该算法首先定义网格结构。在这里，我们使用不同大小的网格结构来更好地平衡定位和空间传播。

在算法2的第2行，解f被随机初始化。为了均匀地采样允许的解空间，我们采用了[5]中描述的初始化策略。具体来说，对于每个$f_p=(a_p，b_p，c_p)$，我们在允许的视差范围[0，dispmax]中选择一个随机视差$z_0$。然后，随机单位向量$n=(n_x，n_y，n_z)$和$z_0$通过$a_p=-n_x/n_z、b_p=-n_y/n_z和c_p=-(n_x{p}_u+n_y{p}_v+n_z{z}_0)/n_z$转换为平面表示。

在第4-13行的主循环中，我们从预定义的网格结构（第5行）中选择一个网格级别$h$，并对所选结构$h$的每个单元（第6-10行）应用算法1的迭代${\alpha }_{ij}$展开式。如第3.3节所述，我们通过划分为由式（15）定义的不相交群来执行迭代${\alpha }_{ij}$展开。由于这种分组，第7-9行的循环中的${\alpha }_{ij}$展开是相互独立的，可以并行执行。

算法1第9行的扰动如[5]所述实现。即，将每个候选标签${\alpha }_{ij}=（a，b，c）$转换为视差$d$和法向量$n$的形式。然后，我们将随机视差${∆}^{\prime }d\in [-r_d，r_d]$和大小为$||{∆}_n^{\prime }|{|}^2=r_n$的随机向量${∆}_n^{\prime }$分别相加，得到$d^{\prime }和n^{\prime }$。我们通过在算法2的第3行设置$r_d\leftarrow dispmax/2和r_n\leftarrow 1$来初始化它们，并在算法2的第12行和算法1的第13行通过$r_d\leftarrow r_d/2和r_n\leftarrow r_n/2$来更新它们。

最后，我们使用[5]中描述的左右一致性检查和加权中值滤波进行后处理，以进一步改进结果。这一步骤在最近的[3]、[5]、[14]、[32]等方法中得到了广泛的应用。

注意，这个算法与我们之前的版本[39]之间主要有两个不同之处。首先，我们删除了[39]的逐像素标签细化步骤。这一步需要更新一个特殊的标签命名空间结构局部共享标签(LSL)用于[39],但可以删除在我们新算法通过使用局部α展开。另一方面，先前的算法是以批处理周期进行的，即它一次生成所有网格结构的所有局部α展开，然后在一次迭代中将它们应用于当前的解$f$。这导致收敛速度慢于我们的新算法，该算法总是从最新的当前解$f$生成每个局部$\alpha$展开。

3.5 Fast implementation

我们的方法有两个主要的计算部分：公式（6）中匹配代价${\varphi }_p(f_p)$的计算，以及GC在算法1中的应用。在第3.3节和第3.4节中，我们已经证明了通过并行执行不相交的局部α展开可以加速后一部分。在本节中，我们将讨论前一部分。

匹配的计算成本${\varphi }_p(f_p)$是非常昂贵的,因为他们需要$O(|W|)$计算为每个术语,$|W|$在哪里匹配窗口的大小。在我们之前的算法[39]中，我们使用GPU。用GPU对我们的方法是合理的，因为${\varphi }_p(f_p)$的所有像素都可以单独计算并行推理,这对比PMBP[3],只能按顺序处理每个像素。然而，计算复杂度是$O(|W|)$，如果我们只使用CPU[39]，它会变得非常低效。

在以下部分中,我们表明,我们可以大约达到$O(1)$的复杂性计算每个${\varphi }_p(f_p)$。观察这里的关键是,我们只需要计算这个成本匹配${\varphi }_p(f_p)$在${\alpha }_{ij}$ -扩张算法1,在${\varphi }_p(f_p)$计算${\varphi }_p$所有$p\in R_{ij}({\alpha }_{ij})$。利用这种一致的标号性质，我们可以有效地结合文献[32]中所使用的快速次区域代价滤波技术，利用该技术可以同时有效地计算所有$p\in R_{ij}$的${\varphi }_p({\alpha }_{ij})$。

更具体地讨论,我们第一次单独${\varphi }_p(f_p)$的计算分为两个步骤:原始匹配的计算成本$${\rho }_{f_p}=\rho (s|f_p)....................................(18)$$
对于支持像素$s\in W_p$，利用边缘感知滤波核${\omega }_{ps}$进行原始匹配代价的聚集

我们还定义了一个过滤区域$M_{i,j}$作为$R_{i,j}$中的联合匹配窗口。

如图6所示，这个$M_{i,j}$通常是一个以$R_{i,j}$为边距的正方形区域，其中$r$像素的宽度围绕$R_{i,j}$，其中$r$为匹配窗口的半径。

在等式（18）的原始匹配部分，计算所有$p\in R_{i,j}$的原始代价${\rho }_{f_p}(s)$，${}^{\forall }s\in W_p$通常需要总计算量$O(|W||R_{i,j}|)$。然而，在一致的标号性质下（即$f_p={\alpha }_{ij}$对于所有$p\in R_{ij}$)，可以通过计算${}^{\forall }s\in M_{i,j}$的${\rho }_{{\alpha }_{i,j}}(s)$对于$O(|M_{i,j}|)$立即计算它们。这里，每个一元项的计算复杂度为$O(|M_{i,j}|/|R_{i,j}|)$。因此，如果$|M_{i,j}|\simeq |R_{i,j}|$，我们可以近似地得到$O(|M_{i,j}|/|R_{i,j}|)\simeq O(1)$[32]。

类似地，如果我们对${\rho }_{{\alpha }_{ij}}(s)$应用常数时间边缘感知滤波${\omega }_{ps}$，则等式（19）的成本聚集部分可以在约$O(1)$中完成，${}^{\forall }s\in M_{ij}$[32]。作为这样一个例子，我们为等式（7）选择了引导图像滤波[13]，但可以使用更复杂的滤波[31]。

注意，由于一致性标签属性是能够使用过滤技术的关键，所以除了使用超像素作为计算单元的[32]外，其他基于PatchMatch的方法[3]、[5]、[14]不能使用该方案。

4. Experiments

在实验中，我们首先在Middlebury基准v2和v3上评估我们的方法。虽然最新的v3基准允许我们与最先进的方法进行比较，但我们也使用较旧的v2，因为有更多的相关方法[3]、[5]、[14]、[32]、[39]仅在此版本中注册。

我们进一步评估了网格尺寸的影响，并与我们之前的方法[39]相比，提出的加速方案的有效性。我们的方法与PMBP[3]、PMF[32]和Olsson等与我们的方法密切相关的[33]方法进行了进一步的比较。补充材料中提供了对更多图像对进行分析和比较的附加结果。

设置
我们在整个实验中使用以下设置。我们使用的台式电脑的核心i7 CPU (3.5 GHz×4物理核心)和NVIDIA GeForce GTX Titan Black GPU。所有方法都使用c++和OpenCV实现。

数据项的参数设置为$\{w,{\tau }_{col},{\tau }_{grad},\alpha \}=\{0.01^2,10,2,0.9\}$在[32]，[36]和[5]之后。匹配窗口w p的大小设置为41×41（即等式(7)中的局部回归窗口$W_k^{\prime }$的大小设置为21×21），这与PMBP[3]和[5]、[14]的设置相同。对于光滑项，我们使用$\{\lambda ，{\tau }_{dis}，\epsilon ，\gamma \}=\{1,1,0.01,10\}$和$N$的八个邻域。

在我们的算法中，我们使用了三个网格结构，单元大小分别为$5\times 5、15\times 15和25\times 25$像素。算法1中的迭代数$\{K_{prop},K_{rand}\}$对于第一个网格结构设置为{1,7}，对于另外两个网格结构设置为{2,0}(仅传播步骤)。除了在4.2和4.7节中，我们禁用了RANSAC提议者与相关方法的公平比较或避免混乱的分析。当启用时，我们为所有网格结构设置$K_{RANS}$ = 1。我们重复主循环十次。我们使用[7]的GC实现。

我们使用两种不同的方法。LE-GF对${\rho }_{ps}$使用了第13节中提出的引导图像滤波。3.2。我们只对这个方法使用一个CPU实现。LE-BF对${\omega }_{ps}$使用双边滤波，${\omega }_{ps}$的定义类似于式（11）和$\lambda =20$，因此能量函数对应于我们在[39]中使用的函数。因此，匹配成本的计算速度与$O(W)$一样慢。在GPU实现中，我们通过在GPU上并行计算每个一元项来加速计算。对于LE-BF和LE-GF，我们使用四个CPU核并行执行不相交的局部α扩展。

4.1 Evaluation on the Middlebury benchmark V2

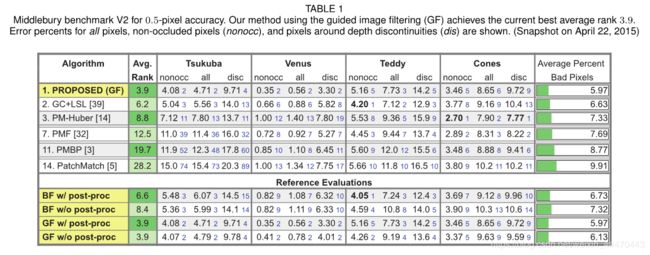
与其他基于补丁匹配的方法[3]、[5]、[14]、[32]、[39]相比，我们在表1中显示了Middlebury立体声基准V2的选定排名，精度为0.5像素。在包括我们以前的方法（GC+LSL）在内的150多种立体声方法中，所提出的LE-GF方法达到了当前最佳av-erage秩（3.9）和坏像素率（5.97%）。即使没有后处理，我们的LE-GF方法在平均秩上仍然优于其他方法，尽管表1中的所有方法都使用后处理。另一方面，由于两种方法以非常相似的方式优化相同的能量函数，因此所提出的LE-BF方法达到了与我们之前的al-gorithm[39]相当的精度。

4.2 Evaluation on the Middlebury benchmark V3

由于与旧版本的主要区别，最新的Middlebury基准引入了更具挑战性的困难，例如高分辨率图像、图像对之间的不同曝光和照明、不完全校正等，因为我们的模型，特别是我们从[5]中借用的数据项，没有考虑到这些新的困难，我们在这里稍微修改了我们的模型，使之适应最新的基准。为此，我们将Zbontar和Lecun的基于CNN的最新匹配成本函数[49]结合在一起，在最新的基准上遵循当前的顶级方法[10]、[20]、[28] 、[29]。这里，我们只将等式（9）的像素级原始匹配代价函数$\rho (\cdot )$替换为它们的匹配代价函数，如下所示。

函数$C_{CNN}(s,s^{\prime })$使用一个神经网络(在[49]中称为MC-CNN- acrt)计算以s和s’为中心的大小为11×11的左右图像块之间的匹配代价。在我们的方法中，我们截断${\tau }_{CNN}=0.5$处的匹配代价值，并使用等式(6)的斜片匹配将其聚合为支持窗口像素$s\in W_p$。除了等式(9)中的变化外，三个网格结构的正方形单元的宽度成比例地改变为图像宽度的1%、3%和9%。由于新基准法规只允许提交一次试验数据，因此我们这里只使用$\lambda =0.5和K_{RANS}=1$的LE-GF方法。我们保留所有其他参数$(i.e.,\{e.W_p,{\tau }_{dis},ϵ,\gamma ,K_{prop},K_{rand}\})$作为默认值。

表2显示了作为默认度量的非遮挡区域的$bad2.0$度量（即，在全分辨率下按2.0像素的错误阈值计算的坏像素百分比）的选定排名。我们的方法不仅在默认度量方面，而且在$\{bad0.5，1.0，2.0，4.0\}\times \{nonocc，all\}$的所有组合$(bad4.0-all除外)$方面都优于表中所有现有的63个方法。在表3中，我们使用训练数据分析了我们的后处理和RANSAC提议者的效果。同样，我们的方法排名第一，即使没有对默认和所有其他坏的非occ度量进行后处理。此外，RANSAC提议者减少了一个点的误差（见第4.7进行更多分析）。avr和stdev表明，通过不同的随机初始化，我们的推理是稳定的。

4.3 Efficient of grid-cell size

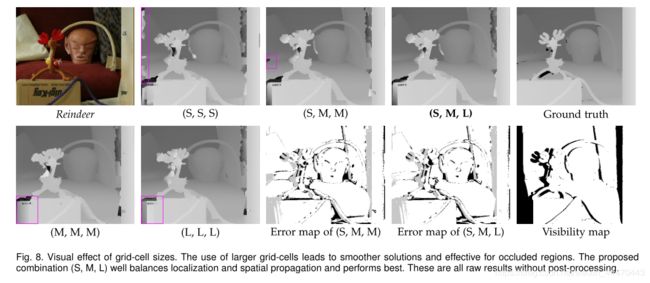
为了观察网格大小的影响，我们使用了5×5像素(即“S”mall)、15×15像素这三种网格大小(以M为单位)，25×25像素(以L为单位)，在不同的组合下，使用以下五种不同的设置来评估性能;$(S,S,S):$所有网格结构的小尺寸单元;$(M,M,M):$所有网格结构的中型单元;$(L,L,L):$所有网格结构的大尺寸单元;$(S,M,M):$分别为第一个和另外两个网格结构的中小型细胞;$(S,M,L):$分别用于第一、第二和第三个网格结构的小型、中型和大型单元格(上述方法的默认设置)。这里，第一个到第三个网格结构的迭代数保持默认值。我们使用了LE-GF方法来获得成本滤波加速度的影响。我们使用$\lambda =0.5$,但保持其他参数的默认值。使用这些设置，我们通过只估计$Reindeer$数据集左侧图像的差异而不进行后处理来观察性能变化。

图7 (a)中的图显示了能量函数值随迭代的变化。图7 (b)中的图显示了亚像素精度下错误率的时间变化。如图所示，多个单元尺寸的联合使用在节能和精度方面都提高了性能。虽然(S, M, M)和(S, M, L)显示了几乎相同的能量跃迁，但所提出的组合(S, M, L)显示出更快和更好的收敛精度。

图8将五个设置的结果与(S, M, M)和(S, M, L)的错误映射进行了比较。使用更大的网格单元有助于获得更平滑的差异，而且对于闭塞区域尤其有效。

与图7 (b)中的运行时间相比，由于成本滤波的开销增加，使用小型单元的效率较低，而使用中型和大型单元的效率几乎相同。

4.4 Efficiency evaluation in comparison to our previous algorithm[39]

我们评估了三种加速技术的有效性：1）不相交α-展开的并行化；2）GPU加速一元成本计算；3）成本滤波。为此，我们比较了以下六种方法：使用一个或四个CPU核（表示为CPUx1和CPUx4）的LE-BF和LE-GF，以及使用GPU和一个或四个CPU核（表示为GPU+CPUx1和GPU+CPUX4）。此外，我们将[39]的算法与CPU和GPU实现（用CPUx1和GPU+CPUx4表示为LSL）进行比较。我们使用$Rocks1$数据集，只估计左图像的差异，而不进行后处理。图9(a)-©分别显示了满标度和缩放标度下的能量值的时间转换，以及亚像素错误率。注意，图9中的能量值由LE-BF和LSL的能量函数进行评估，以便更好地可视化。

CPU上局部α扩展的并行化： 通过比较CPUx1和CPUx4，我们观察到LE-BF和LE-GF的加速约为3.5倍。注意，LE-GF的收敛能量值相对较高，因为它优化了不同的能量函数。然而，如果我们看到图9©，它实际上在这个例子中找到了更好的解决方案。另一方面，LE-BF从GPU+CPUx1到GPU+CPUx4的速度限制在1.7x左右。这是因为一元成本计算已经被GPU并行化了，这种加速是由其他部分的并行化来解释的，比如成对项和最小割的计算。

GPU上一元成本计算的并行化: 通过比较GPU+CPUx1和LE-BF的CPUx1，我们得到了大约19x的加速。这相对于我们之前的LSL方法的32x的加速要小，主要是因为GPU数据传输的开销比较大。

成本快速过滤: 通过比较LE-GF和LE-BF方法，我们发现CPUx1和CPUx4两种版本的速度都提高了5.3倍。值得注意的是，即使是CPU实现的LE-GF (CPUx4)也可以达到几乎与GPU实现的LE-BF (GPU+CPUx1)相当的效率。

与我们之前的方法[39]比较: 与之前的LSL方法[39]相比，在相同的单核结果(CPUx1)下，我们的LE-BF算法比LSL算法收敛速度快得多。我们认为主要有三个因素导致了这种加速;首先，[39]采用的批处理循环算法使其收敛速度变慢;其次，利用代价滤波，在O(1)中计算式(18)的第一步，而[39]在O(|W|)中分别计算每一一元项;最后，我们删除了[39]的每像素标签细化步骤，这需要额外的单位成本计算。从LSL (GPU+CPUx4)到LE-BF (GPU+CPUx4)也可以观察到类似的加速。

4.5 Comparison with PMBP[3]

我们将我们的方法与最接近我们的方法PMBP[3]进行了比较。为了进行公平的比较，我们在式(5)中对N使用四个邻居作为PMBP的相同设置。一个平滑的体重进行比较与默认设置(eight-neighbor N),我们使用λ= 40 LE-GF LE-BF和λ= 2,并保持其他参数为默认。对于PMBP，我们使用与我们相同的模型;与原始PMBP唯一不同的是平滑项，它不满足Eq.(2)的子模块性。在PMBP中，它为每个像素定义了K个候选标签，我们设K = 1, K = 5(原始论文使用K = 5)。我们使用锥数据集进行比较，只估计左图像的差异，不进行后处理。

图10 (a) - ©分别显示了能量值在全尺度和缩放尺度下的时间变化，以及亚像素错误率。我们使用它的GPU和CPU(一个或四个CPU核心)实现来展示我们的方法的性能。对于PMBP，我们也在GPU上实现了一元成本计算，但是由于数据传输的开销，计算速度变慢了。在文献中没有针对PMBP的高效GPU实现。因此，图中显示了使用单个CPU核心的PMBP结果。图10 (a)和(b)显示，即使使用一个cpu核心实现，我们的LE-BF和LE-GF的收敛性也可以与PMBP相比，甚至更快。通过CPU和GPU的并行化，我们的算法比PMBP算法的收敛速度快得多。此外，我们的方法达到较低的能量和更大的精度比PMBP在收敛。在图11中，我们比较了我们的LE-GF方法和PMBP的结果，K = 5。当PMBP产生噪声差异时，我们的方法在边缘和闭塞区域发现更平滑和更好的差异。

4.6 Comparison with PMF[32]

我们还使用与我们相同的数据项将我们的LE-GF方法与PMF[32]进行了比较。对于PMF，超像素K的数量被设置为[32]中使用的300、500和700(在[32]中K = 500是默认值)，我们充分迭代30次。LE-GF和PMF都使用一个CPU内核运行。

图12 $(a)$-$(c)$分别显示了能量值在全尺度和缩放尺度下的时间变化，以及亚像素错误率。如图12 (a)和(b)所示，PMF收敛于比我们更高的能量，因为它不能显式地优化成对光滑项，因为它是一个局部方法。此外，虽然PMF的能量几乎是单调下降的，但经过多次迭代后，精度的跃迁并不稳定，甚至会下降。这也是由于缺乏显式的平滑正则化，PMF收敛于一个坏的局部极小值。图13比较了我们的方法和K=500的pmf的结果。同样，我们的方法发现边缘和遮挡区域的差异更平滑和更好。

4.7 Comparison with Olsson et al.[33]

们与Olsson等人的立体方法[33]进行了比较，我们借用了平滑项。与我们的方法不同的是，他们的数据项没有使用精确的倾斜patch匹配，而是使用传统的基于融合的优化方法，使用基于RANSAC的局部平面拟合生成的平面方案(详见[33])。为了比较我们和[33]的优化方法，我们将[33]的数据项替换为我们的数据项，使两种方法使用与我们相同的能量函数。在这里，我们使用了我们的LE-GF方法的两个变体，删除了RANSAC提议者和正则化项，它们是与[33]密切相关的组件。我们禁用所有方法的后处理。

表4显示了Middlebury V2中的Teddy和V3中的另外三个数据集的错误率，其中提出的方法性能优于[33]和其他方法。如图14和图15所示，我们的方法比[33]具有更快的收敛速度和更好的光滑表面质量。空间标签的传播不仅加快了推理速度，而且引入了隐式平滑效应[5]，帮助我们的方法找到更光滑的表面。无论RANSAC的提议者是谁，我们的方法基本上都表现得相当好，优于[33]。另一方面，RANSAC的提议者促进了收敛性(见图14)，也有效地恢复了Vintage中无纹理的大平面(图16)。使用更高级的提议者[34]可能会导致进一步的改进。还要注意的是，除了表4中的Vintage之外，我们的方法在没有正则化的情况下也可以很好地处理非闭塞区域(与[33]相当)。仅倾斜的patch匹配项就具有隐式的二阶平滑效果[5]，而[33]的正则化器进一步加强了它，尤其是对于闭塞或无纹理的区域。

5. Conclusion

本文提出了一种用于连续三维平面标签估计的精确有效的立体匹配方法。与以往使用融合移动[25]、[33]、[45]的方法不同，我们的方法是子问题最优的，只需要随机初始解。通过与最新的连续MRF立体成像方法PMBP[3]的比较，表明该方法具有效率高、精度高等优点。使用基于GC的优化器使我们的方法具有优势。

此外，利用局部立体方法PMF[32]开发的子区域代价滤波方案，实现了比PMF更快的算法和更高的精度。如[32]所示，我们的方法将更快地使用更轻量级的常量时间过滤，如[31]。

后续工作[18]，[40]表明，我们的优化策略可以用于更一般的对应场估计，而不是立体。我们还认为，使用GC[23]、[44]的遮挡并行方案可以整合到我们的框架中，从而获得更高的精度。

Appendix A

证明：为了完整起见，我们用符号重复了[33]中给出的原始证明。关于${\overline{\psi }}_{pq}\left(f_p,f_q\right)$
$\begin{array}{rl}{\overline{\psi }}_{pq}(\alpha ,\alpha )+{\overline{\psi }}_{pq}(\beta ,\gamma )& ={\overline{\psi }}_{pq}(\beta ,\gamma )\\ & =\left|d_p(\beta )-d_p(\gamma )\right|+\left|d_q(\beta )-d_q(\gamma )\right|\\ & =\left|\left(d_p(\beta )-d_p(\alpha )\right)-\left(d_p(\gamma )-d_p(\alpha )\right)\right|+\left(d_q(\beta )-d_q(\alpha )\right)-\left(d_q(\gamma )-d_q(\alpha )\right)|\\ & \le \left|d_p(\beta )-d_p(\alpha )\right|+\left|d_p(\gamma )-d_p(\alpha )\right|+\left|d_q(\beta )-d_q(\alpha )\right|+\left|d_q(\gamma )-d_q(\alpha )\right|\\ & ={\overline{\psi }}_{pq}(\beta ,\alpha )+{\overline{\psi }}_{pq}(\alpha ,\gamma )\end{array}$

因此，${\overline{\psi }}_{pq}\left(f_p,f_q\right)$满足展开运动的子模性。因为它的截断函数
$\begin{array}{rl}\min \left({\overline{\psi }}_{pq}(\alpha ,\alpha ),\tau \right)+\min \left({\overline{\psi }}_{pq}(\beta ,\gamma ),\tau \right)& =\min \left({\overline{\psi }}_{pq}(\beta ,\gamma ),\tau \right)\\ & \le \min \left({\overline{\psi }}_{pq}(\beta ,\alpha )+{\overline{\psi }}_{pq}(\alpha ,\gamma ),\tau \right)\\ & \le \min \left({\overline{\psi }}_{pq}(\beta ,\alpha ),\tau \right)+\min \left({\overline{\psi }}_{pq}(\alpha ,\gamma ),\tau \right)\end{array}$
因此${\overline{\psi }}_{pq}\left(f_p,f_q\right)$也满足子模性。

Appendix B

Additional result

我们在这里提供了额外的结果来分析网格单元大小(第4.3节)和并行化(第4.4节)的影响，以及与PMBP$[3]$(第4.5节)、PMF$[32]$(第4.6节)和Olsson等人的$[33]$(第4.7节)方法的比较。我们通过显示运行时的错误率转换图来评估性能，其中错误率由所有区域的bad 2.0度量来评估。为了提供不同的示例，我们使用了Middlebury V3训练数据集中的15对图像。

除非另有说明，否则所有方法都运行在一个cpu核心上，以优化与我们在第4.2节中用于基准v3评估的相同的能量函数。我们方法的设置也与我们在第4.2节中使用的相同。在所有方法中都禁用后期处理。

网格大小的影响
图A1显示了对网格单元大小影响的分析。与第4.3节相似，我们比较了拟议的网格单元组合(S, M, L)与其他四种组合(L, L, L)、(M, M, M)、(S, S, S)和(S, M, M)。对于大多数图像对，所提出的组合(S, M, L)在五种组合中表现最好。

并行化效率比较
图A2显示了我们的局部展开移动算法的并行化分析。当我们的方法在四个CPU核上并行执行时，我们观察到15对图像中平均加速3.8倍。

与PMBP[3]比较
图A3将我们的方法与PMBP[3]进行了比较。与第4.4节相似，我们将PMBP(使用K = 1和5)与我们的方法的两个变体(使用引导图像滤波(GF)和双边滤波(BF)进行了比较。由于PMBP不能使用GF的代价映射滤波加速，因此我们只使用BF进行PMBP。因此，我们的方法使用BF优化与PMBP相同的能量函数，而我们的方法使用GF优化不同的函数。所有方法都使用四个相邻的成对项作为PMBP的相同设置。

如图A3所示，我们的算法在收敛精度上均优于PMBP算法，而我们的算法在收敛速度上优于其他算法。我们的方法可以通过并行化得到进一步的加速，如图A2所示。

与PMF[32]比较
图A4将我们的方法与PMF[32]进行了比较。两种方法使用相同的能量函数，但PMF只能优化其数据项。通过显式正则化，我们的方法对所有图像对的性能始终优于PMF。

与Olsson等人的[33]比较
图A5将我们的方法与Olsson等人的方法进行了比较。两种方法使用相同的能量函数，但优化方法不同。对于大多数图像对，我们的方法比[33]方法快6倍左右，达到可比较或更好的精度。我们的方法可以通过并行化得到进一步的加速，如图A2所示。