论文《Poor textural image tie point matching via graph theory》学习

《基于图论的低纹理图像连接点匹配》2017

Abstract

特征匹配的目的是寻找相应的点作为图像之间的连接点。当输入图像具有低对比度或包含重复模式、遮挡或同质纹理时，鲁棒匹配仍然是一项具有挑战性的任务。本文提出了一种基于图论的特征匹配算法。该算法将几何约束和辐射约束结合到一个边缘加权（EW）亲和张量中。然后通过高阶图匹配得到连接点。测试了覆盖森林、沙漠、荒地和城市地区的四对低纹理图像。为了进行比较，还使用了三种最新的匹配技术，即尺度不变特征变换（SIFT）、加速鲁棒特征（SURF）和加速分段测试（FAST）。实验结果表明，在不同类型的不良纹理中，SIFT、SURF和FAST得到的匹配召回率在0~35%之间。然而，通过几何和辐射测量的结合以及电子战策略，该算法在四对图像中的召回率都优于50%。更好的匹配召回提高了正确匹配的数量、分散性和位置准确性。

1. Introduction

连接点匹配是计算机视觉、模式识别、摄影测量和遥感中的一项基本任务。本任务旨在寻找重叠区域的稀疏特征对应（Hartmann等人，2016）。当图像具有独特而丰富的纹理时，辐射信息足以匹配精细的连接点。然而，遥感图像的纹理通常很差。森林、荒地、沙漠和城市地区是容易产生不良纹理的环境的例子。森林图像在小尺度上具有重复模式，裸地图像具有同质纹理，沙漠图像具有少量纹理，城市图像具有遮挡和不连续性。从局部外观的角度来看，“差纹理”表示两个共轭区域之间的低对比度或非线性灰度变化。因此，在匹配低纹理图像时仅使用辐射信息是不够的，有时需要人工干预。这些干预措施将阻碍连接点匹配的自动化。

现有的匹配算法可以分为两类。第一类是基于辐射信息的算法，如归一化互相关（Gonzalez and Woods，1992）、SIFT（Lowe，2004）和基于特征阶的自相似（Sedaghat and Ebadi，2015）。当图像纹理精细且与众不同时，这些匹配算法是有效的（Krystian和Cordelia，2005）。第二类包括集成辐射和几何信息的匹配算法；这些算法包括半全局匹配（Heiko，2008）、基于补丁的多视图立体（Furukawa和Ponce，2007）和多照片几何约束匹配（Zhang和Armin，2006）。这些匹配算法利用预先确定的几何信息作为辅助匹配约束。这种集成方法的目的是在一定的约束条件下，首先将匹配问题分解成若干个子问题，然后通过迭代过程得到匹配结果，直到所有子问题收敛于同一解或相似解。

对于低纹理的图像关联点匹配，国内外研究较少。吴等人（2012）集成点和线特征，以获取基于多个视图的相机几何先验知识的三维密集点云。Zickler和Efros（2007）使用主成分分析SIFT（PCA-SIFT，Ke和Sukthankar，2004）对部分遮挡低对比度纹理中的目标进行检测，取得了满意的结果。低纹理图像匹配中另一个常用的算法是线特征匹配，例如线相交上下文特征（Kim and Lee，2010）、平均-标准偏差线描述符（Wang et al.，2009）、线段匹配（LSM，Bay et al.，2005）和具有同形约束的LSM（Sun et al.，2015）。这些算法在结构丰富的图像中检测线特征，然后用线描述符对线特征进行匹配。然而，在遥感图像中并不总是呈现直线特征。

差的纹理图像匹配在以下方面仍然是一个具有挑战性的任务。首先，纹理的均匀性通常表现为低的局部图像对比度；因此，基于辐射测量的匹配方法受到噪声的干扰。基于辐射测量的连接点匹配算法，如SIFT、SURF（Bay et al.，2006）和FAST（Mair et al.，2010），无论是从正确匹配的数量还是在位置精度方面，都无法提取理想的连接点。第二，纹理重复由规则的像素级递归表示，特征描述子不明显。因此，这些方法容易产生不正确的匹配。第三，纹理遮挡通常会导致阴影区域的局部几何变形和非线性密度变化。此外，两个共轭区域之间的辐射特征描述子距离不够近。纹理匹配不良的主要问题是正确匹配不足、不匹配和大量不正确匹配。

基于图的连接点匹配算法（Chung，1997）的主要思想是将图像特征作为图节点。然后将特征匹配问题转化为节点对应问题，通过图匹配解决（Livi和Rizzi，2013）。主要用于图形匹配的几何约束可以分为三类：酉约束（或点约束）、边约束（或对约束）和三元组约束（或三角形约束）。在这三种类型中，成对约束是最受关注的。这些约束编码图边中两个点集之间的关系。成对约束通常嵌入在图匹配算法中，例如谱图匹配（Leordeanu和Hebert，2005）、分级分配（Gold和Rangarajan，1996）、概率图匹配（Egozi等人，2013）和平衡图匹配（Schólkopf等人，2006）。三元组约束可以利用图的三角形信息。它们是局部仿射不变约束，而成对约束仅是距离不变约束。高阶图匹配（HOGM，Duchenne等人，2011）是一种典型的三重约束算法。当存在大量的异常点时，上述所有的图匹配算法都会产生很差的匹配结果。Cho等人。（2014）提出了一种最大池策略来处理异常值，但仅使用成对约束。Torresani等人。（2008）将图匹配算法应用于图像特征对应中；但是，由于仅使用成对约束，因此结果不是仿射不变的。因此，本文提出了一种基于高阶亲和张量的匹配算法，并将两个图之间的关系编码在张量中。与传统的辐射几何积分算法相比，该算法有三个显著的差异。（1） 几何信息在匹配中起着类似于辐射信息的作用，而不是作为辅助约束。（2） 匹配结果在几何和辐射测量上都是全局最优的。以SIFT匹配为例，最近邻距离比（NNDR）是一种有效的匹配方法，但它在辐射测量中仅是全局最优的。（3） 匹配算法采用边缘加权的亲和张量，使得匹配对异常点具有鲁棒性。

本文的其余部分安排如下。第二节主要介绍了图匹配的方法和提出的EW亲和张量。第三节给出了匹配方法的详细实现流程和实验结果。第四节得出本研究的结论。

2. Methodology

该部分提出了一种新的EW-HOGM方法来解决低纹理图像匹配问题。第2.1节介绍了HOGM的概念。第2.2节介绍了拟议的EW-HOGM。第2.3节描述了合成数据的实验结果。第2.4节对计算复杂性进行了理论分析。

2.1. HOGM

图像关联点匹配是指两组特征之间的对应关系，这个过程可以定义为一个图匹配问题。如图1所示，从源图像和目标图像中提取五对图像特征。图像特征可以看作是图形的节点，而位置、灰度等特征字符是节点的属性。两个特征之间的关系，如角度和距离，可以看作是图的边。两个图像特征集的匹配问题是两个图的节点匹配问题。因此，将连接点匹配问题转化为图匹配问题。

给出了两个图像特征集P和Q及其对应图GP和GQ。如果节点$V_i\in G_P$和$V_{i^{\prime }}0\in G_Q$是赋值，那么$f_i\in P和f_{i^{\prime }}\in Q$是连接点，反之亦然。图匹配问题可以表述为

其中C是赋值集；nP和nQ是两个特征集的特征数；$i和i^{\prime }$是节点$V_i和V_{i^{\prime }}$的标签，它们表示本文中的节点索引；$c_{i{i}^{\prime }}$是C的赋值元素，它表示$V_i$对应于$V_{i^{\prime }}$。图节点的关系（即对应关系）也可以用分配矩阵来表示

其中$z_{i{i}^{\prime }}^{\ast }=1$表示Vi对应于Vi’，$z_{i{i}^{\prime }}^{\ast }=0$表示Vi与GQ中的任何节点都不匹配。如图2所示，图匹配问题根据其约束形式可分为三类：一阶、二阶和高阶（三阶或更高）图匹配问题。

在一阶矩阵$A\in I{R}^{n_P\times n_Q}$上建立了一阶图匹配问题


一阶图匹配问题为下列目标函数找到最优解：

其中$a\in I{R}^{n_P{n}_Q}$是矩阵A的行向量化，1表示所有元素为一的向量；Z是位于连续向量空间中的软赋值矩阵，$Z^{\ast }\in \{0,1{\}}^{n_P\times n_Q}$是硬赋值矩阵。因此，将Z离散为二元矩阵需要额外的过程，通常选择的离散方法是贪婪算法（见算法1，Leordeanu和Hebert，2005）。


在等式（3）中，$Z1<=1；Z^{T}1<=1$对匹配的对应关系施加限制。GP的每个节点在GQ中最多有一个对应的节点，GQ的每个节点在GP中最多有一个对应的节点。公式（3）可以使用匈牙利算法（Edmonds，1965）求解，也可以通过动态规划近似求解（Belongie等人，2002）。

一阶图匹配中使用的酉相似性仅对辐射变化（如SIFT和SURF等图像特征描述符）不变。
如图2所示，给出了两条边$E_{ij}\in G_p$和$E_{i^{\prime }{j}^{\prime }}\in G_Q$以及两个节点对$Vi、Vj\in E_{ij}$和$V{i}^{\prime }、V{j}^{\prime }\in E_{i^{\prime }{j}^{\prime }}$。与点相似性度量类似，成对相似性度量可以用${\Omega }_2={\Omega }_2(c_{i{i}^{\prime }}；c_{j{j}^{\prime }})$表示。在成对约束下定义的关联矩阵由

其中$w^{\ast }$是矩阵A的主特征向量，最终的解可以使用算法1来实现。
值得注意的是，点约束与成对约束兼容。在式（4）中，如果i=j且i’=j’，则边缘相似性${\Omega }_2(c_{i{i}^{\prime }}；c_{j{j}^{\prime }})$等于$Omeg{a}_1(c_{i{i}^{\prime }})$。因此，在二阶图匹配中，点态相似度可以集成到边缘相似度中。边缘相似性除了对辐射变化具有不变性外，对旋转也具有不变性。

然而，一阶和二阶图匹配对尺度和小仿射变换都不具有不变性。因此，二阶图匹配应该扩展到高阶（三阶或更高阶）。为了简单起见，以三阶图匹配为例。类似于点相似性和对相似性，三重态（三角形）相似性可以定义为




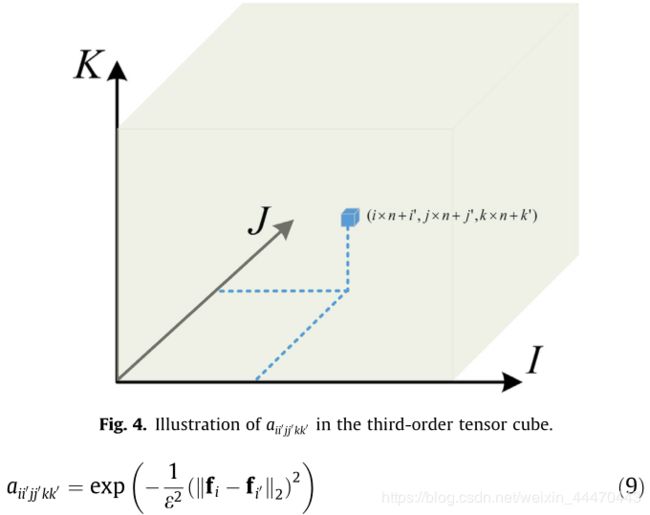
式（9）将辐射信息集成到三阶亲和张量中；因此，式（8）在几何和辐射测量方面是全局最优的。

然而，点态相似性与辐射特征描述符（例如128维SIFT描述符或36D SURF描述符）相关，而三重态相似性与几何信息（即3D三角形描述符）相关。因此，这两种相似性度量具有不同的物理维度，应标准化为统一的度量框架：

此外，规范化描述符比三角形描述符更具特色，因为它们具有更多的维度。因此，在描述词之间需要一个平衡因子，如下所示：

四。结论和今后的工作

图像匹配是遥感图像配准、空中三角测量和目标检测的基本步骤。虽然它在纹理丰富的图像中得到了很好的解决，但由于纹理的均匀性、重复性、遮挡性和不连续性，在匹配纹理较差的图像时仍然是一个挑战。传统的算法由于只使用辐射信息而容易失败。本研究提出一种新的匹配演算法，将几何与辐射资讯整合成亲和张量，并利用电子战策略来处理离群值。该方法包括四个步骤：特征检测、图形生成、张量构造和高阶图匹配。在特征检测中，采用了UR SIFT、SIFT和ANN，并将提取的图像特征作为图节点。然后，用表示节点和三角形相似性的元素构造亲和张量。将EW策略嵌入到幂迭代中，使匹配对异常点具有鲁棒性。利用四对不同纹理类型的遥感图像对该方法进行了评价：高层建筑、森林、沙漠和裸地。SIFT、SURF、FAST等基于特征的匹配算法的匹配召回率均低于35%，而ewogm的匹配召回率则高于50%。由于该算法具有较高的匹配召回率，因此在实验数据的正确匹配、离散度和位置精度方面都能获得可靠的匹配结果。

当考虑到EW-HOGM算法对孤立点的容忍度时，该算法也可用于形状匹配和三维云配准，其中孤立点的数量很大。此外，如果适当修改，ewogm也可以应用于粗差检测。但是，还有一些问题需要进一步解决。由于亲和张量的巨大增加了幂次迭代的运算量，EW-HOGM的计算复杂度较高。进一步的研究可以引入新的策略，使张量稀疏化，降低幂迭代的计算复杂度。此外，power迭代也可以在基于GPU的并行计算框架中实现（Silva等人，2016），这可以极大地加快power迭代的速度。