人工智能 --- Python求解线性和非线性规划问题
基于jupyter notebook的Python编程
1、线性规划中的单纯形法、大M法的excel求解、python编程求解和python包求解；
2、非线性规划的拉格朗日乘子法的手工数学推导、python编程和python包求解；
一、线性规划问题求解
1、Excel中大M法与Excel的“规划求解”包对实际问题的求解比较
实际例题：
求解以下约束条件的线性规划的最大值和最优解
使用大M法对实际问题的求解
使用Excel的“规划求解”包对实际问题的求解
在Excel中将数据及相应的公式写入到Excel里
通过Excel自带的“规划求解”功能，将结果求解出来
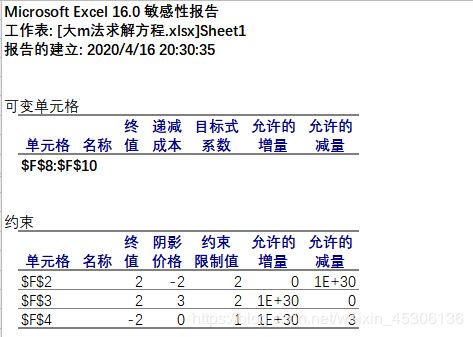
2、Python求解线性规划问题
2.1 新建txt文档，填入线性回归分析标准化模型
新建txt文档，写入标准化模型系数，如下所示
2.2 Python使用单纯法对实际线性规划问题的求解
python 代码如下
import numpy as np #导入相应的库
import sys
def solve(d,bn):
while max(list(d[0][:-1])) > 0:
l = list(d[0][:-2])
jnum = l.index(max(l)) #转入下标
m=[]
for i in range(bn):
if d[i][jnum] == 0:
m.append(0.)
else:
m.append(d[i][-1]/d[i][jnum])
inum = m.index(min([x for x in m[1:] if x!=0])) #转出下标
s[inum-1] = jnum #更新基变量
d[inum] /= d[inum][jnum]
for i in range(bn):
if i != inum:
d[i] -= d[i][jnum] * d[inum]
def printSol(d,cn):
for i in range(cn - 1):
if i in s:
print("x"+str(i)+"=%.2f" %d[s.index(i)+1][-1])
else:
print("x"+str(i)+"=0.00")
print("objective is %.2f"%(-d[0][-1]))
d = np.loadtxt("F:/data.txt", dtype=np.float)
(bn,cn) = d.shape
s = list(range(cn-bn,cn-1)) #基变量列表
solve(d,bn)
printSol(d,cn)
运行结果：
x0=0.00
x1=1.00
x2=3.00
x3=0.00
x4=2.00
x5=0.00
x6=0.00
objective is 32.00
2.3 Python使用scipy库对实际线性规划问题的求解
整体代码如下：
#导入包
from scipy import optimize
import numpy as np
#确定c,A_ub,B_ub
c = np.array([1,14,6])
A_ub = np.array([[1,1,1],[1,0,0],[0,0,1],[0,3,1]])
B_ub = np.array([4,2,3,6])
#求解
res =optimize.linprog(-c,A_ub,B_ub)
print(res)
运行结果：
con: array([], dtype=float64)
fun: -31.99999999819265
message: 'Optimization terminated successfully.'
nit: 4
slack: array([6.62327970e-11, 2.00000000e+00, 3.88720167e-10, 3.41993101e-10])
status: 0
success: True
x: array([3.06911596e-10, 1.00000000e+00, 3.00000000e+00])
从代码中可以发现
c：c指的应该是要求最大值的函数的系数数组
A_ub：A_ub是应该是不等式未知量的系数矩阵,也就是不等式左边
B_ub：B_ub就是不等式的右边了，也就是不等式右边
3、结果对比分析
3.1 单纯形法结果
3.2 scipy结果
通过对两个的结果分析，可以看出单纯形法的结果更加具体，因为结果为整数；对于SciPy库，其运算结果为小数，是否更加具体不知道，但是两个的运算结果相差不大，其误差也比较小，所以可以选择忽略。
二、非线性规划问题的求解
1、等式约束下的拉格朗日乘子法
公式推导：这里只是简单的放了一张图片对等式约束下拉格朗日乘子法的求解步骤进行了讲解。
2、Python实现对带约束的非线性规划求解
求解实际例题
2.1 Python编程实现求解
Python代码：
#导入sympy包，用于求导，方程组求解等等
from sympy import *
#设置变量
x1 = symbols("x1")
x2 = symbols("x2")
alpha = symbols("alpha")
#beta = symbols("beta")
#构造拉格朗日等式
L = 60 - 10*x1 - 4*x2 + x1*x1 + x2*x2 - x1*x2 - alpha * (x1 + x2 - 8)
#求导，构造KKT条件
difyL_x1 = diff(L, x1) #对变量x1求导
difyL_x2 = diff(L, x2) #对变量x2求导
difyL_alpha = diff(L, alpha) #对alpha求导
#求解KKT等式
aa = solve([difyL_x1, difyL_x2, difyL_alpha], [x1, x2, alpha])
print(aa)
运行结果：
{x1: 5, x2: 3, alpha: -3}
2.2 python使用SciPy库实现求解问题
python代码如下：
from scipy.optimize import minimize
import numpy as np
#目标函数：
def func(args):
fun = lambda x: 60 - 10*x[0] - 4*x[1] + x[0]**2 + x[1]**2 - x[0]*x[1]
return fun
#约束条件，包括等式约束和不等式约束
def con(args):
cons = ({'type': 'eq', 'fun': lambda x: x[0]+x[1]-8})
return cons
if __name__ == "__main__":
args = ()
args1 = ()
cons = con(args1)
x0 = np.array((2.0, 1.0)) #设置初始值，初始值的设置很重要，很容易收敛到另外的极值点中，建议多试几个值
#求解#
res = minimize(func(args), x0, method='SLSQP', constraints=cons)
print(res.fun)
print(res.success)
print(res.x)
运行结果：
17.000000000000007
True
[4.99999994 3.00000006]
3、Python求解结果对比分析
3.1普通法求解结果
3.2 scipy库求解结果
