Gaussian process的样本生成与其mean和kernel的联系

 

转自https://zhuanlan.zhihu.com/p/31427491

1. 给定mean和covariance，如何生成一个GP。

当给定mean function和kernel的时候，我们可以确定唯一的GP，但是唯一的这个GP却有着无穷多个样本，比如

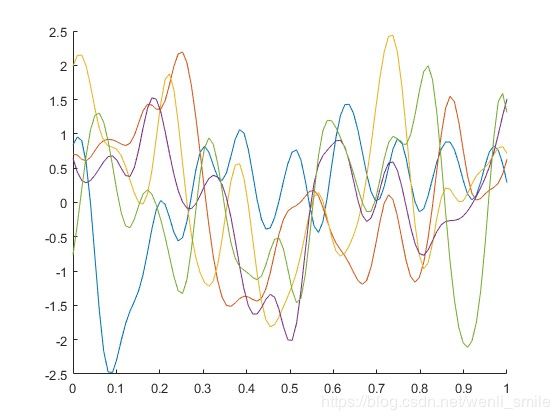
                                      5条样本曲线

这个的五条曲线都是来自于一个的确定参数的mean function（零均值）和确定参数的kernel（Squared Exponential, ell = 0.04, sf = 1）的GP的。当然你还可以画出50条，500条，甚至无穷多条GP的样本，不过归根到底他们都是来自同一个确定的GP。

或者你会问，这些乱七八糟的线，看上去没有任何规律呀！

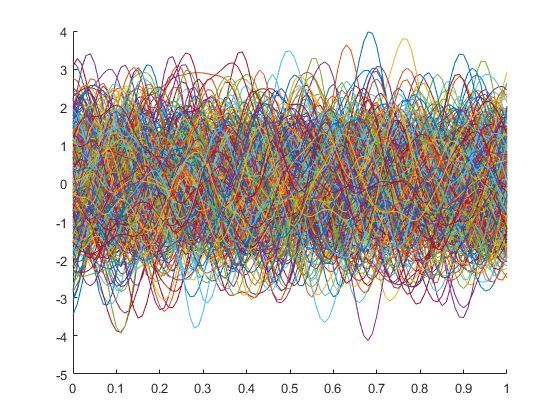
的确，画五条的时候，还没有看不出规律，但是你若是画上500条呢？

                                            500条样本曲线

嗯，似乎好像还是杂乱的曲线呀，这能有什么规律呀？

“真的没有呀！”

再仔细看看！

“似乎好像那些曲线似乎都在-2到2之间波动”

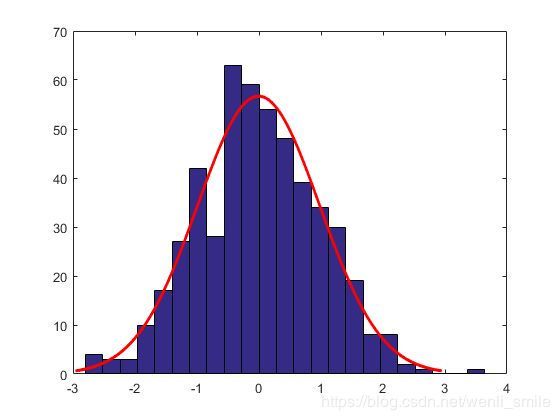
对嘛，其实这就是规律！如果我们随便挑选一个横轴x=0.5去寻找对应的500个样本中每一个对应的x=0.5的点，然后画个直方图，一切就明了了！

                                500样本中所有x=0.5的直方图

看着是不是还蛮像我们最开始说的高斯分布的的直方图呀？

什么？还是不像！

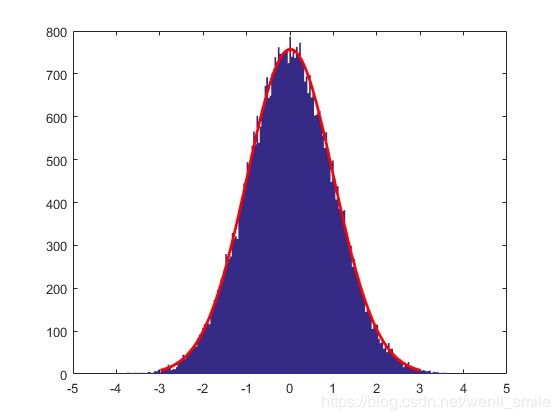
好吧，那一定是因为这个500不够，来个50000的吧！

这次看着是不是像了很多呢？再仔细观察是不是发现这个高斯分布也不是一个普通的高斯分布，而是一个以0为均值，以1为方差的高斯分布哦！

这个也可以做实验得到么？

当然，其实只要直接把之前50000个点的数据用MATLAB自带的函数一fit就知道啦

[muhat,sigmahat] = normfit(data)
[muhat,sigmahat,muci,sigmaci] = normfit(data)
[muhat,sigmahat,muci,sigmaci] = normfit(data,alpha)

没错，这个数值的结果就是mean = 0, variance = 1。回过头来再想一下，这个0是什么呢，这个0其实就是我们之前给定的mean function在x=0.5处的值（其实因为是常数0，所以无论x等于多少，都是0）呀，而这个1呢，其实就是之前我们给定的kernel，Squared Exponential, 当x=0.5时自己与自己的covariance（其实就是方差啦）！

PS： 当然可能数字取的太随意的，0太普通，没有标示性，有兴趣的话，你可以将之前的mean function设置成为任意的非零数，看看之后对应的高斯分布的均值是不是也会相应移动哦！

 

wow，原来那么神奇呀！

汗！

其实一点也不神奇，这一切都是因为之前我们给出的GP的定义呀！

从理论的角度看，根据GP的定义，连续输入空间（时间或者是空间）中每个点都是与一个高斯分布的随机变量相关联，换言之就是，在任意一个时间或者空间点上，对应的随机变量都是满足高斯分布，而这个被满足的高斯分布的里面的决定量（mean和variance）又是被对应的高斯过程的中的mean function和covariance function所确定的。

因而才会发生之前我们所观察到情况，即在50000条样本曲线的x=0.5处的所有可以估计出一个被确定均值和方差的高斯分布，因为在我们开始生成GP样本前，mean function和kernel是预先给定的！

 

原来如此呀！可是生成GP的过程和代码呢？

别急，这就来！步骤如下：

1. 给定mean function和covariance（kernel） function，比如最简单的mean默认为constant，且为0，,kernel = Squared Exponential(SE)。
2. 给定mean function以及kernel中的hyperparameter的初始值，比如，mean是constant，一点为0那就是处处为0了，kernel =SE, 需要给出其中的 (这个表述跟gpml一致，并且这个代码包中也允许mean为空，即使用mean=0，Documentation for GPML Matlab CodeDocumentation for GPML Matlab Code)。
3. 给定想要产生的样本函数定义域，比如问题图中的范围[0,1]，如果是计算程序的，自然还涉及到取多少个点，比如在给定的[0,1]每隔0.01去一个点总共101个输入点。
4. 有了mean function和kernel以及对应的初始超参数，那么我们就可以计算对应的mean function 的均值向量，记为M， kernel的covariance matrix，记为C。
5. 对C进行SVD分解，。
6. 从标准高斯分布中产生n个点的样本，这里n就是输入点的个数，记为。
7. 则利用 就可以生成一个给定具体mean function和kernel的GP的样本。

当然如果要问为什么这样生成的东西就是GP，那其实只要计算mean和covariance就好，原因在于下面这个定理（详见https://arxiv.org/pdf/1605.07906.pdf）[3]

所以， ,，因此就可以说明这就是以上GP的一个样本。

简单的给个基于gpml工具包的函数代码（代码需要先加载gpml的startup，切记切记，不然代码可是动不了哈）：

meanfunc = @meanConst; m = 0; hyp_mean = m;
% meanfunc = @meanLinear; a = 2; hyp_mean = 2;
% 这里也可以使用gpml包里面的其他mean function

covfunc = @covSEiso; ell = 0.04; sf = 1; hyp_cov = log([ell,sf]);
% 这里也可以使用gpml包里面的其他kernel

x = 0:0.01:1; x=x';
n = size(x,1);

M = feval(meanfunc,hyp_mean,x);
C = feval(covfunc,hyp_cov,x);

[u,s,~] = svd(C);  %SVD decomposition, C=usv'
gn = randn(n,1);  % Genearate a sample from standard normal distribution
z_gp = u*sqrt(s)*gn + M; 

 

不难吧？

必须的！

有了这个基本的代码，重复50000次，获得50000条样本区别不用我继续详细说了吧？

然后给定任意一个输入点，看看对应的点整体是不是服从一个特别的高斯分布！

非常建议仍然不是很理解的小伙伴们，可以动手试一试哈！

 

最后在说说再简单关于实际用GPR的进行预测时候，如何处理mean function的设定问题。其实这是一个理论上重要的问题，但是实际操作中经常默认取常数值0。

 

首先我们需要明确是的，在运用GPR做预测的时候，我们假定是：给定的样本来自一个参数待定的确定形式GP的一个样本（即对应无穷多条样本曲线中的一条），这里注意的是，假定是来自的高斯过程，不是说一定需要来自高斯分布哦（这个话题下一节我们还要仔细讨论）！然后根据训练集，学习得出给定mean function和kernel的形式所对应具体的超参数。这里的学习依据有很多种方法，但是说到底，并不是唯一可以被确定的。

也就是说给定有限个数据点，通过学习后，可以得到的一个最有可能的归属GP（当然根据不同的学习，得出所归属的GP也并非同一个），而不是一个唯一确定的归属GP。所以这也就导致了给定一组数据，它既可以看做是mean=0的某一个GP，也可以看做对应其他mean function对应的另一个GP。当然若是看做mean=0的某一个GP，各种计算都要方便简单很多。所以说如果可能的话，我们当然要选择一个简单的啦！

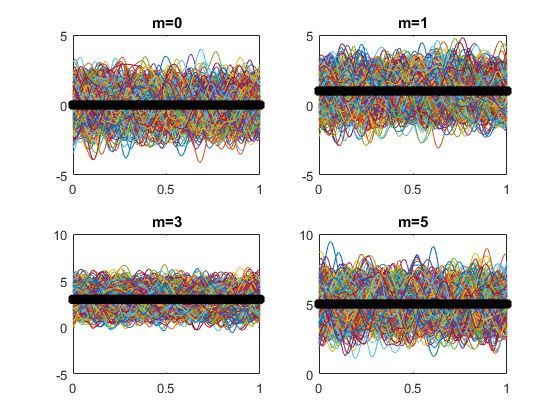
另外，对于mean来说，比如constant， 不同的constant最后在样本的体现上很明显吧，如下图所示

mean function是constant,但对应的常数值不同

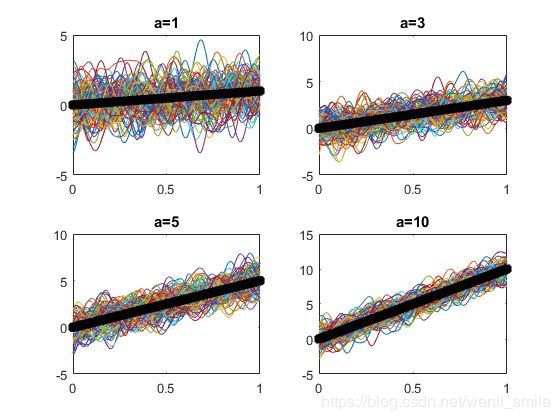
其实，也就是把所有样本整体进行的平移！也正是如此，那么方便起见，我们在处理数据的时候只要将数据先做一些基本的预处理，比如归零化处理后，那么我们假设mean=0的也是合情合理吧！当然如果有明显的其他特征也是先行除掉哈，比如线性，下图就是用了不同斜率的linear mean function所产生的。

Linear mean function对应不同斜率值

究其本质，事实上就是公式（1）中的求期望是对于随机变量的，而关于x的函数此时就是个常数，而常数的期望就是它本身，因而最终样本产生事实上就是  ，即mean=0的部分外加一个给定的mean形式。

 

当然如果一定要加入非零mean function也是合理的，然后需要增加待确定参数，而这一切的压力就是转嫁到之后的参数学习的步骤中，增加计算量，而效果一般而言也并非会有本质提升。当然一些长期的预测模型中，整体而言，由于GPR最后回归于给定mean function，所以其实这种情况下，mean的给定也代表了对长期未来的一种先验。具体的一部分学术上讨论的并不是很多，可以参考文献[1][2]。

 

总而言之，对以GPR模型的使用中，最好先对数据进行预处理（事实上，这也是大多数数据分析是所必须的），然后再没有特殊要求的情况下，选择零均值函数的GPR模型即可，因为这是最常用的选择也是性价比最高的选择！

 

 

参考文献

[1] Roberts, Stephen, et al. "Gaussian processes for time-series modelling." Phil. Trans. R. Soc. A371.1984 (2013): 20110550.

[2] Chen, Zexun. Gaussian process regression methods and extensions for stock market prediction. Diss. Department of Mathematics, 2017.

[3] Chen, Zexun, and Bo Wang. "How priors of initial hyperparameters affect Gaussian process regression models." arXiv preprint arXiv:1605.07906 (2016).