机器学习西瓜书复习 - 5 集成学习
1 说明
关于集成学习，目前还没有学完，梯度上升树的算法只看了一点，直方图那些连看都没有看，但是拖的已经够久了，近期的时间用来整理自然语言处理的论文了，暂时也没有精力去深入学习其他集成学习方法，先把已经涉及过的部分复习写好，还没有复习到的地方，进行标注。
1.1 目录
加粗的部分只进行了部分复习，后续有时间再进行补上
2 集成学习方法简述
2.1 bagging
2.2 boost
2.3 学习方差和学习误差
3 AI研习社手势分类任务
3.1 任务说明
3.2 利用箱图数据分析
3.3 使用svm进行数据分析
3.4 使用集成学习方法进行数据分析
2 集成学习方法简述
- 集成学习方法，就我的理解而言，说简单也简单，说复杂也复杂。
- 简单来说，基本的思路是用多个学习器来替代单一的学习器
- 其中复杂的是，选取什么样的学习器，如何集成多个学习器
- 我是这样理解的，集成方法中的学习器集合，学习到的是原本的任务的一个子集，就好比去一个孤岛找人，单学习器的目标是训练出一个优秀的情报员，而多学习器的目标是训练出多个合格的情报员，假设我们对这个孤单所知极少，那么三个合格的情报员分头搜索很可能比一个优秀情报员很快的找到目标。
- 按照上述的理解，对于集成方法可以粗浅地用两种划分来表征，其一是样本上的划分，其二是学习目标上的划分。比如，三个情报员分头寻找，即是对样本的划分；第一个情报员搜索之后，发现岛上很多沼泽，并把自己的经验传授给第二个情报员，第二个情报员携带穿越沼泽的设备，并且调整了学习的目标，重点搜索沼泽附近的人，即是对学习目标的划分。
2.1 bagging
2.1.1基本过程：
- 在样本集中进行有放回的随机采样，进行m次采样得到一个样本划分，再执行k轮，得到k个样本划分
- 分别对k个样本划分训练k个学习器
- 使用投票法、求平均值法等组合方法，组合k个学习器的输出，得到最终的结果
2.1.2 一些理解
- 问题1：为何bagging能提升学习能力
A 从自然语言的角度来看，bagging很像是分头搜索，一个人负责一个区域，再将单个个体所学到的知识组合起来，对于单个区域而言，单独的分配一个人，能了解到区域内更加细节的信息，因此，这个组合对于整个孤岛的了解会更加全面。尽管一个完美的情报员能够迅速搜索出孤岛上所有的目标，但是实际上，完美的样本集是不存在的，因此也不可能在不完美的样本集上训练出完美的情报员。所以，直观上来看，对整个孤岛的了解更全面的bagging方法，学习能力更强
B 从学习的角度来说，极端情况下，学习器的数量为样本的总数，这时候训练误差为0，很明显，这个时候模型过拟合了，但是从另一个角度来看，模型也学习到了样本的所有特征
C 同时，多个学习器采取组合的方式来决定最终的输出，对于异常值来说，大部分学习器都会将其排除掉，学习器的鲁棒性更强
- 问题2： 为何进行有放回的随机采样
A 有放回的随机采样是基于样本划分的bagging方法的核心，这是我个人的理解
B 从自然语言的角度来看，随机采样，即三个情报员搜索的路线是随机的；有放回的采样，即三个情报员的搜索路线可能有重复的，结合起来，即随机选出三块足够大的区域，将三个情报员分别派出到三个区域搜索
C 从学习的角度来说，引入随机性，模型的泛化能力越强
D 对于引入有放回的采样，其一，不放回采样的情况下，样本划分互斥，切蛋糕一样把样本切开，这样的划分很可能是不合理的。其二，放回采样时，单个学习器能学到更全面的知识，提升了单个学习器的能力。其三，放回采样时，一个样本可以被多个学习器学习到，相当于从多个维度上对样本进行了学习。
问题3： 如何进行样本划分？
A 对样本进行随机有放回的采样：单个学习器仅使用部分样本
B 对特征进行随机有放回的采样：单个学习器仅使用部分特征
C 对样本和特征皆进行随机有放回的采样：单个学习器仅使用部分特征和部分样本，比较典型的应用便是随机森林
D 根据自己的需求自定义采样规则：根据自己的需求设计采样规则，应该是有效的，比如我进行手势数据的分析时，先筛选出了一分部分异常样本，采样的时候，单个学习器只能得到一部分类别的异常样本，尽管事实证明没什么用，但是也是一种尝试
2.2 boost
2.1.1 基本过程：
- 选择一个基础学习器，比如决策树学习器，在样本数进行训练
- 基于第一个基础学习器的结果，对样本分布进行调整，重点关注第一个学习器犯错的样本
- 再选择一个基础学习器，在调整过的分布上进行学习
- 重复以上过程
2.1.2 一些理解
问题一：为何boost方法能提升学习能力？
显而易见，每一轮学习之后，犯错的样本数越来越少，相对应的模型的偏差也会越来越少，学习能力相比单个学习器而言，是要强的。正因为如此，boost方法中，对于基础学习器的学习能力要求也相对低一些
问题二：如何设计boost方法？
A boost方法从直观上来理解很简单，每一步都针对上一步进行优化，但是如何根据实际情况来设计优化的目标并不是一件简单的事，这里了解的不多，暂时不写了，下次复习再写。
2.3 学习方差和偏差
以前对于方差和误差的理解都有些模糊，这里整理一下，以免下次再踩坑
2.3.1 第一阶段的理解：打靶图
对于方差的理解
方差是稳定程度，像是开枪射击靶子，弹孔都挨的很近，则方差小，离的很远，则方差大，对应于方差与均值的公式如下：
对于偏差的理解
偏差代表的是准确程度，如果弹孔越接近十环，则偏差越小，反之，则偏差越大
2.3.2 第二阶段的理解：学习方差和学习偏差
对于方差的理解
方差是训练误差和测试误差之间的相似表征，方差越小，训练误差与测试误差越接近，方差越大，训练误差与测试误差差别越大
对于偏差的理解
偏差主要是针对训练误差，这里考虑到训练效果不好的情况，测试效果也不会好。偏差越小，训练误差越小，偏差越大，训练误差越大
2.3.3 第三阶段的理解：bagging和boost
对于方差的理解
A 由上所述，我理解的bagging方法是对样本进行全面的学习，用多个学习器深入到样本的方方面面，再在组合学习器的过程中，筛选出样本中最本质的特征。直观上来看，bagging方法中引入更多的学习器，那么引入了更全面的样本信息，同时也引入了更多随机性，一方面学到了关于样本的更多知识，另一方面，也缓解了过拟合的问题
B 这里引用一下随机森林算法的作者的话，你可以往随机森林之中加入任意多的树，随机森林不会过拟合。随着树的增多，越能突出样本的有效信息，减少噪音的作用，自然，测试结果跟训练结果会更加的接近，从而方差更小了
C 因此，方差与模型拟合度联系到了一起，用以缓解过拟合的方法能从减少方差的角度来理解
- 减少特征：过拟合时，引入更少的特征，目的是学到样本更泛化的特征
- 增加样本数量： 过拟合时，引入更多数据，目的是对样本有全面的了解
- 引入正则化项：引入的正则化是对样本的一个先验猜测，如果猜测合理，那么训练集和测试集则有了一部分天然的共同点
- 剪枝：提早结束训练，目的是保持一个更泛化的结果
无论是对样本进行更泛化的认识，还是更全面的认识，方差太大的模型在训练集跟测试集上的表现会更相近，方差会更小、
D 需要注意的是，实际应用中随机森林是会过拟合的，这样的结论显而易见，找一个例子跑一下就知道了，而随机森林的作者所说的那番话，是过于自信，还是有其他的考虑，暂时不清楚，下次复习的时候，可以再来思考一下。
对于偏差的理解
A 这部分理解起来相对简单一些，从boost方法的每一轮结果来看，一个合理的boost方法，每一轮都会提升其在训练集上的表现，如果不考虑过拟合的情况，一直迭代下去，训练集上的偏差会越来越小
B 以梯度提升树为例，先介绍概念
- 提升，即boost，意思是每一轮的新增的树都是要提升整体模型的表现
- 梯度，即每一轮进行提升时，朝着目标函数负梯度的方向前进，显然，这是让每一轮得到的提升最大化
- 对树进行梯度下降优化的概念不是那么直观，用一个图说明一下：
C 梯度提升树的优化过程中，累计学习器F对训练集的拟合效果越来越好，同时偏差越来越小，与方差偏大对应了过拟合类似，偏差偏大，对应的欠拟合。因此，可以从缓解欠拟合的角度来理解偏差
增加特征：与过拟合中的减少特征的作用类似
减少正则化项：与过拟合中的增加正则化项的作用类似
增加模型复杂度：直观上来看，就是梯度提升树引入的梯度优化方法，以及神经网络引入更多的层，以模型复杂度为代价，得到的是训练集上错误率的减少，即偏差减少了
3 AI研习社手势分类任务
3.1 任务说明
详见AI研习社官网：URL1
官网上有数据集，数据说明，并且还有一些高分的源码，源码没来得及看，等把西瓜书都复习完再来学习
3.2 利用箱图数据分析
3.2.2 生成箱图
A 将训练集中的各个类别的手势数据全部取出来，并对数据进行归一化处理
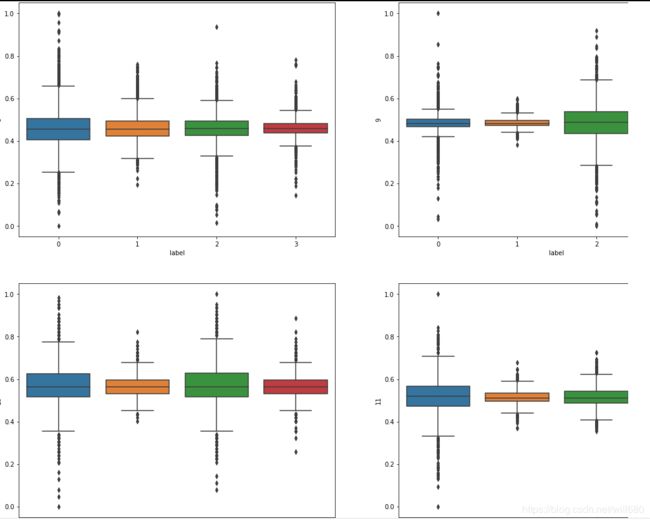
B 使用seaborn的boxplot方法，依次对单个特征生成箱图，箱图如下所示
其中横坐标label代表四种手势，纵坐标是每一个特征归一化之后的值，一共64个箱图，这里截出几个
3.2.3 箱图数据分析
A 第一次尝试
- 作为一个新手，面对这64张没有明显差别的图，没有什么头绪，于是直接用svm跑了一遍数据，效果很差
- 之后对异常值进行分析，先是将单个特征的异常值所在的行号都取出来，再对行号取并集，发现所有的数据集都是异常的，只能放弃
B 第二次尝试
- 开始考虑部分特征的组合，并且观察到每个传感器的对应信号的箱图相似度很大，比如1号传感器的1号信号，2号传感器的1号信号，以此类推。于是将对应的特征单独拿出来对比，如下图所示
- 此外，为了进一步验证这些特征之间的关联性，对这些特征组合进行异常值分析，得到的结果如下
显然，异常值数量大多在1000以下，不到总数据集的10%
C 观察到这个信息之后，脑子里第一反应就是集成学习的方法，于是便将这个练习搁置下来，作为集成学习复习时候的练习题
3.3 使用svm进行数据分析
3.3.1 实验设置
A 学习器使用的是最简单的基于核函数的svc，凭直觉简单选取了一些参数，代码放在下面了
def svm_factory():
svms = []
for c in [10,100,400]:
classifier_weight = SVC(C=c,cache_size=1000,class_weight={1: 3})
svms.append((classifier_weight,'c:'+str(c)))
classifier = LinearSVC(C=c,class_weight={1: 3},random_state=7, tol=1e-6,max_iter=1000000)
svms.append((classifier,'LinearSVC'+str(c)))
return svms
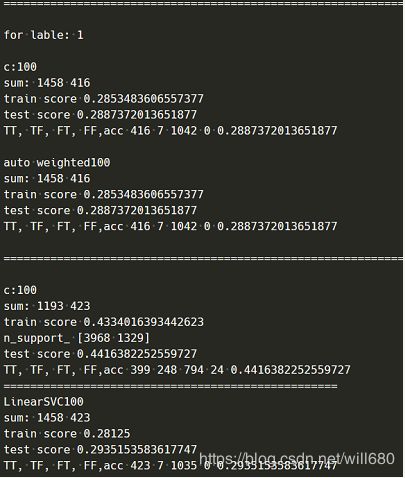
B 测试数据是8个传感器的第三个信号，其中一些异常数据已经被筛除，标签的设置是依次选取一个手势作为正类，其他手势作为负类。具体的部分测试结果如下所示：
C 上面截取了几个简单的学习器的测试结果，很明显，无论是基于核方法的SVC还是线性SVC，进行第0个手势的分类表现要远远优于其他手势的分类表现（这里仅仅列出了第一个手势的分类）。原本下一步要进行基于svm的bagging方法的训练了，但是时间有限，一番思索，这些工作还是留待下次复习，先用sklearn的随机森林的API观察一下效果
3.4 使用集成学习方法进行数据分析
3.4.1 实验设置
A 用的是sklearn的标准随机森林作为学习器，考虑到这个数据集的特点主要是特征，简单起见，仅选取 max_features 参数可调，其他参数默认
B 使用梯度提升树，AdaBoostClassifier，LogisticClassifier作为对比
C 不对数据集进行异常值处理
3.4.2 实验结果
A 先给出结论，不经过任何调优，由于这个数据集的特殊性，随机森林是要优于梯度提升树的，下面给出具体结果
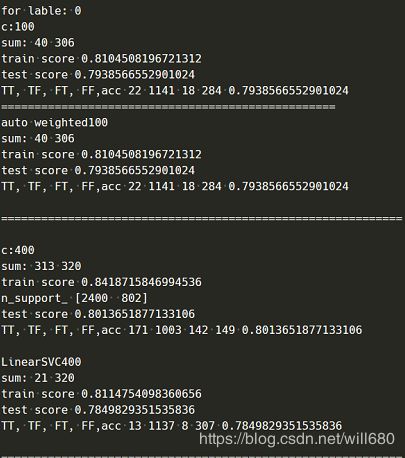
B 由上图可知，对于这个任务
- 集成方法的表现远远要好于单学习器
- 随机森林在训练集上的表现很优秀，测试集上也比梯度上升树稍好
C 回到之前提到过的随机森林是否会过拟合的问题，这里使用了更大的n_estimators做了一个对比
- 很明显，随机森林过拟合了
- 值得注意的梯度上升树的表现效果大幅度提升，符合其学习器越多，偏差越低的特点。同时，这个任务上面，没有做任何的优化，梯度上升树在训练集和测试集上都得到了很好的效果
参考：
AI研习社手势分类任务 https://god.yanxishe.com/14 URL1
https://www.cnblogs.com/maybe2030/p/4585705.html 随机森林的一些概念解释
https://blog.csdn.net/u010429286/article/details/100101768 随机森林过拟合证明
https://www.cnblogs.com/yanshw/p/12112243.html 机器学习中非正式的偏差与方差的概念