数据结构_栈及其应用
栈及其应用
栈
栈是存放数据对象的一种特殊容器,栈中的元素始终遵循后进先出的顺序,作为一种抽象数据类型,栈支持的操作接口如下:
stack栈的应用
- 逆序输出
输出次序与处理过程颠倒;递归深度和输出长度不易知道。
conversion(进制转换)
void convert(stack<char>&s,_int64 n,int base)
{
static char digit[]={'0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'};
while(n>0)
{
s.push(digit[n%base]);//余数对应的数位入栈
n/=base;
}
}
int main()
{
stack<char> s;
convert(s,n,base);
while(!s.empty())
cout<- 递归嵌套
具有自相似性的问题可递归描述,但分支位置和嵌套深度不固定。
stack permutation+parenthesis(栈混洗和括号匹配)
1、括号匹配
消去一对紧邻的左右括号,不影响全局的匹配判断。

顺序扫描表达式,用栈记录已经扫描的部分,反复迭代:凡遇到”(“,则进栈;凡遇到”)“,则出栈。

bool paren(const char exp[],int lo,int hi)
{
stack<char>s;
for(int i=0;iif(exp[i]=='(') //左括号入栈
s.push(exp[i]);
else if(!s.empty())
s.pop();
else
return false;
}
return s,empty();//最终,匹配时栈空。
} 2、栈混洗
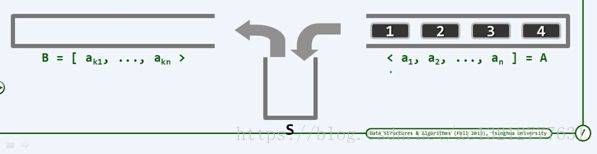
只允许将A的顶元素弹出并压入s,或将s的顶元素弹出并压入B中,经过一系列以上操作后,A中的元素全部转入B中,则称之为A的一个栈混洗。
对于有n个元素而言他的栈混洗个数记为sp(n);则可以由如下过程推出sp(n)的递推式:
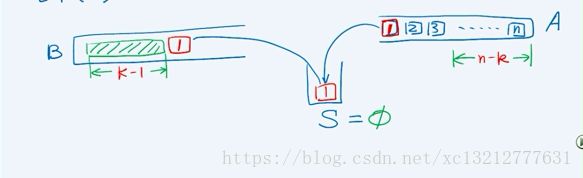
当第一个元素作为第k个元素被推入栈B中时,此时中转栈应该为空,栈A中还剩下n-k个元素。因为,此时栈B中的K-1个元素的栈混洗个数与剩下的n-k个元素的栈混洗个数相互独立。则可以推出:

栈混洗的甄别:
我们可以知道任意三个元素能否按照某种相对次序出现于混洗中,与替他元素无关,因此可以推出:
![]()
对于上述条件反过来也成立,只要任意序列中不含上述形式,就是一种栈混洗。
算法:直接借助栈A,B和S,模拟栈混洗过程,每次在S.pop()之前,检测S是否为空;或需要弹出的元素在S中,却不是顶元素。
example:
1、栈的压入、弹出序列
题目描述:输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。
分析:实际上这就是一个栈混洗的过程,我们使用上述描述的算法就可以解决。即:如果下一个弹出的数字刚好是辅助栈S的栈顶数字,那么直接弹出。如果下一个弹出的数字不在栈顶,我们把压栈序列中还没有入栈的数字压入S中,直到把下一个需要弹出的元素压入栈顶为止。如果所有元素都压入了栈还没有找到下一个弹出的数字,那么该序列就不是一个栈混洗。
class Solution {
public:
bool IsPopOrder(vector<int> pushv,vector<int> popv) {
stack<int> s; //辅助栈S
int id=0;
for(int i=0;iwhile(s.empty()||s.top()!=popv[i])
{
s.push(pushv[id++]);
if(id>pushv.size())
return false;
}
s.pop();
}
return true;
}
}; 栈混洗与括号匹配之间的联系,n个元素的栈混洗有多少种,n对括号所能表达的合法表达式就有多少种。
将左括号换成push操作,右括号换成pop操作,
由n对括号构成的一个合法的表达式可以解释为对n个元素进行栈混洗的合法的过程。

2、包含min函数的栈(扩展应用)
题目描述:定义栈的数据结构,在该类型中实现一个能够得到栈的最小的元素的min函数。
首先最直观的是我们可以想到在栈里添加一个成员变量存放最小的元素。每次压入一个新元素的时候,如果比当前元素还要小,就更新最小元素,但是这时候会存在一个问题,如果当最小元素被弹出栈后,没法获得下一个最小元素,以此推广,我们借助一个辅助栈S,它用来记录栈A中每一个元素作为栈顶元素时,栈的最小元素。也就是说,我们把每一次的最小元素都存起来。
class Solution {
public:
void push(int value) {
m_data.push(value);
if(m_min.size()==0||valueelse
m_min.push(m_min.top());
}
void pop() {
m_data.pop();
m_min.pop();
}
int top() {
return m_data.top();
}
int min() {
return m_min.top();
}
private:
stack<int> m_data;
stack<int> m_min;//构造辅助栈 相当于记录的m_data中的每一位元素作为栈顶元素时,栈中的最小值是多少,若用一个变量记录最小值,当其弹出时,无法在得到最小值。
}; - 延迟缓冲
在线性扫描算法模式中,在预读足够长之后,方能确定可处理的前缀。
evaluation(表达式求值)
该算法自左向右扫描表达式,并对其中字符逐一做相应的处理。那些已经扫描过但是因信息不足尚不能够处理的操作数与运算符,将分别缓冲至栈opnd和栈optr中。一旦判定以缓存的子表达式优先级足够高,便弹出相关的操作数和运算符,随机执行运算,并将结果压入栈opnd中。
#define N_OPTR 9 //运算符总数
typedef enum { ADD, SUB, MUL, DIV, POW, FAC, L_P, R_P, EOE } Operator; //运算符集合
//加、减、乘、除、乘方、阶乘、左括号、右括号、起始符与终止符
const char pri[N_OPTR][N_OPTR] = { //运算符优先等级 [栈顶] [当前]
/* |-------------------- 当 前 运 算 符 --------------------| */
/* + - * / ^ ! ( ) \0 */
/* -- + */ '>', '>', '<', '<', '<', '<', '<', '>', '>',
/* | - */ '>', '>', '<', '<', '<', '<', '<', '>', '>',
/* 栈 * */ '>', '>', '>', '>', '<', '<', '<', '>', '>',
/* 顶 / */ '>', '>', '>', '>', '<', '<', '<', '>', '>',
/* 运 ^ */ '>', '>', '>', '>', '>', '<', '<', '>', '>',
/* 算 ! */ '>', '>', '>', '>', '>', '>', ' ', '>', '>',
/* 符 ( */ '<', '<', '<', '<', '<', '<', '<', '=', ' ',
/* | ) */ ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ',
/* -- \0 */ '<', '<', '<', '<', '<', '<', '<', ' ', '='
};
float evaluate ( char* S, char*& RPN ) { //对(已剔除白空格的)表达式S求值,并转换为逆波兰式RPN
Stack<float> opnd; Stack<char> optr; //运算数栈、运算符栈
optr.push ( '\0' ); //尾哨兵'\0'也作为头哨兵首先入栈
while ( !optr.empty() ) { //在运算符栈非空之前,逐个处理表达式中各字符
if ( isdigit ( *S ) ) { //若当前字符为操作数,则
readNumber ( S, opnd ); append ( RPN, opnd.top() ); //读入操作数,并将其接至RPN末尾
} else //若当前字符为运算符,则
switch ( orderBetween ( optr.top(), *S ) ) { //视其与栈顶运算符之间优先级高低分别处理
case '<': //栈顶运算符优先级更低时
optr.push ( *S ); S++; //计算推迟,当前运算符进栈
break;
case '=': //优先级相等(当前运算符为右括号或者尾部哨兵'\0')时
optr.pop(); S++; //脱括号并接收下一个字符
break;
case '>': { //栈顶运算符优先级更高时,可实施相应的计算,并将结果重新入栈
char op = optr.pop(); append ( RPN, op ); //栈顶运算符出栈并续接至RPN末尾
if ( '!' == op ) { //若属于一元运算符
float pOpnd = opnd.pop(); //只需取出一个操作数,并
opnd.push ( calcu ( op, pOpnd ) ); //实施一元计算,结果入栈
} else { //对于其它(二元)运算符
float pOpnd2 = opnd.pop(), pOpnd1 = opnd.pop(); //取出后、前操作数
opnd.push ( calcu ( pOpnd1, op, pOpnd2 ) ); //实施二元计算,结果入栈
}
break;
}
default : exit ( -1 ); //逢语法错误,不做处理直接退出
}//switch
}//while
return opnd.pop(); //弹出并返回最后的计算结果
}
- 栈式计算
基于栈结构的特定计算模式。
RPN(逆波兰表达式)
RPN表达式(后缀表达式):在由运算符和操作数组成的表达式中,不适用括号,即可以表示带优先级的运算关系,RPN表达式中运算符的执行次序,可以更为简洁的确定,既不必在事先做任何约定,也不用括号强制改变优先级。

由中缀表达式转换为后缀表达式:
1、手工转换

对于运算数的顺序而言,不会改变,操作数在中缀表达式和后缀表达式中一致。
2、转换算法
凡是遇到操作数,即追加至RPN;而运算符只有在从栈中弹出并且执行时,才会被追加。

example:
请实现如下接口
/* 功能:四则运算
* 输入:strExpression:字符串格式的算术表达式,如: "3+2*{1+2*[-4/(8-6)+7]}"
* 返回:算术表达式的计算结果
*/
public static int calculate(String strExpression)
{
/* 请实现*/
return 0;
}
约束:
pucExpression字符串中的有效字符包括[‘0’-‘9’],‘+’,‘-’, ‘*’,‘/’ ,‘(’, ‘)’,‘[’, ‘]’,‘{’ ,‘}’。
pucExpression算术表达式的有效性由调用者保证;
#include