虚数的几何意义
它是一个数学概念，用来套套公式就行。
它在高等物理里面才会用到，所以别担心，到大学你就明白了。
如此教学怎么能激发出孩子学习数学的热情呢!所以今天我们将借助以下几种工具来攻克虚数这个概念：
关注数学概念间的联系，而非公式。
将虚数概念的引进看做 数学系统的扩展，就像 零、小数、负数的概念一样。
还有我们的秘密武器：类比式的学习。我们将从虚数的前辈，负数开始讨论。负数与虚数的比较如下（图就不翻了哈哈）：
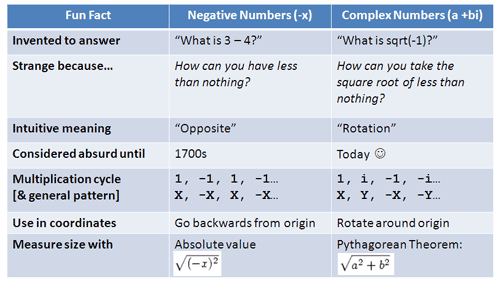
如果这会儿还看不懂，那就暂时先放一边。到最后我们会把一切都弄清楚的。
情景回放：
我们真的理解负数吗？
负数的概念并不简单。想象自己是1700年的一个欧洲数学家。你有3和4，你可以知道4-3=1.很简单。但是3-4 该怎么办？这个运算到底什么意思呢？你怎么能从3头牛中拿走4头牛？你如何拥有比 没有还少的东西？
负数曾被认为荒谬之极，它“玷污了整个等式理论”（Francis Maseres, 1759）而今天，认为负数不合逻辑而且没用才是荒谬的。问问你数学老师负数有没有颠覆数学的根基。
为什么呢？我们创造了一个 有用的 理论数。负数看不见摸不着，但是却能很好地描述一些特定的关系（如债务）。所以它是有用的。
比如说“我欠你30”，如果要记下来的话，我会写下“-30”，说明我欠了钱。
如果我挣了钱，还了债，（-30+100=70）我可以很容易把交易过程记录下来，现在我有+70，说明我没有欠债。
正数和负数自动地跟随着方向，你不必特意去描述每次交易的作用。计算也变得更简单，更优雅。负数是否是“有形的”并不重要，它很有用处，也成为了我们日常计算的一部分。
但负数概念的却来之不易：这是一场宏大的思想变革，即使是欧拉，发现了 e 常数及其他伟大成就的数学巨人，也不能像今天的我们一样理解负数。
直面虚数
虚数有着相似的身世。我们很容易求出这样的方程解：
很多人第一次看到这个方程的时候都懵了。你想让一个数的平方小于零？太荒唐了！
看起来的确很疯狂，就像 负数，零，无理数，刚进入人们视野时一样。这个方程看起来毫无意义，不是吗？
你错了。所谓的“虚数”和其他数一样正常，它们同样是描述世界的工具。只要 -1，0.3,和0 存在，就让我们假设存在一个数使得
一个数乘以它本身等于-1，这是怎么回事呢？
好吧，这确实有点头疼。“让我们假装它存在”的把戏的确让数学变得简单又优雅。新的逻辑可以更轻松地描述某个概念。
你可能不接受i的存在，就像当年那些古板的数学家不接受-1一样。
新颖，费脑的概念总是不能立即被人理解，即使他是欧拉。但如同负数那样，这些陌生的概念仍然有它的用处。我不喜欢管它叫“虚数”，这简直是种侮辱、讽刺，令人扫兴。数字 i和别的数字一样，但是“虚数”的叫法沿袭下来，所以我们还是如此称呼它。
负数和复数的图形化理解
等式x^2=9意味着：
变换x 为何值时，经过两次变换能将1变成9？
答案是"x=3"和"x=-3"。
现在看看方程x^2=-1,经过什么变换x两次后，1变成了-1？
把一个正数平方显然不对，因为结果是正数。
把一个负数平方也不对，两个负数相乘结果会翻转成正数。
但如果进行的是旋转变换呢！听起来不靠谱，但是想象一下x代表“旋转90度”，经过两次x变换可以得到一个180度的旋转，正好把1翻转成-1！
再想想，我们还可以从其他方向讲1 变成-1 ，“负”旋转或者乘以 -i
如果我们两次 乘以 -i，就会把 1 变成 -i ，把 -i 变成 -1 所以-1 的平方根是 i和 - i。
看上去很酷。我们已经有了方程的解，但是它有什么用呢？
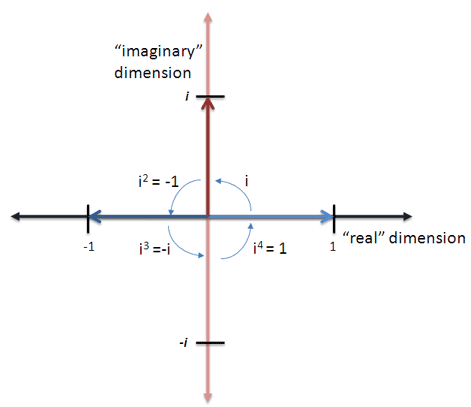
i 是用来衡量数字 的一个“新的虚构维度”
i 或-i 代表了经过旋转后的数字。
乘以 i 代表 旋转逆时针90度
乘以 -i代表旋转顺时针90度
经过同一方向的两次旋转后结果为 -1 ，回到了只有正数和负数的”正常“维度。
数字是二维的。有点伤脑筋，想当年分数和长除法也让古罗马的人伤透了脑筋（1和2 之间才不会还有数字呢！）。
当我们提问”如何用两步把1 变成-1 ?“,我们已经有了答案:经过两次90度旋转。这是一种思考数字的全新视角。但是它很管用（顺便提一下，复数运算的几何意义在复数出现几十年后才被发现）。出于习惯我们规定逆时针旋转90度为正。
找规律
我们再深入一点。当你连乘一个负数（如-1），你会得到形如：
1, -1, 1, -1, 1, -1, 1, -1的数列
因为-1 不会改变数字的大小，只会改变符号，运算结果会在正负间不来回变换。对于任意数“x”，你可以得到数列：
x, -x, x, -x, x, -x…
数x 可以代表周期，假设周期在 好坏之间来回变换，如果此时是一个好的周期，那么47个周期之后会是好还是坏呢？
-x代表了坏周期。注意负数是如何保持符号的——我们把 -1^47按进计算器里而不需要掰着手指头算（老外真SB。）
现在如果我们连乘 i会怎么样呢？
对数列求值
（三次逆时针旋转等于一次顺时针旋转）
（四次旋转得到一个完整的周期）
（新的周期）
表达成图形就是：
四个旋转为一周期。明白了吗？小孩子都知道4个转向与没转时方向一样。在看下面这个数列：
X, Y, -X, -Y, X, Y, -X, -Y…
如同负数的翻转模式一样，虚数可以使一个数在两个维度“X”和"Y"之间旋转。
理解复数
一个数有可能即是“实”的，又是“虚”的吗？
当然。谁说我们只能转90度？如果我们有一个数它是实部为1，虚部也为1，看上去是这样：
我们就有了一个45度角，它的实部和虚部大小相等。
事实上我们可以用虚数和实数的结合来代表角度。这个角 的意义是“旋转角”。既有实部又有虚部的数称为复数，写作a+ib 的形式。
a 是实部，b是虚部。
计算实部和虚部的大小，因为这样不能从整体上衡量复数。
让我们退一步想想。负数的大小也不是掰着手指头数出来的——它代表了负数和零点间的距离。负数的大小计算如下：
也即计算绝对值，那么对于复数而言，如何计算两个相差90度的部分呢？当然是毕达哥拉斯定理。我们讲实部和虚部构造成一个直角三角形，其斜边就是到原点的距离：
计算复数的大小虽然没有“去掉负号”那样简单，但是复数的大小很有用处。请看一个列子。
一个实例：旋转
不用等到学大学物理时再使用复数运算，今天我们就搞定它。关于复数的乘法可讲的内容很多，但是请记住一点：乘以一个复数就是按照复数的角度进行旋转。
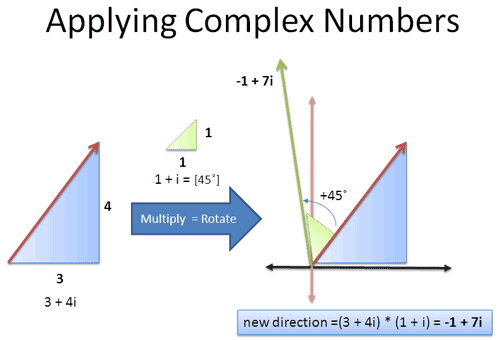
我们来看一个例子：假设我有一艘船，船头朝向偏东3个单位而偏北4个单位的方向。如果我逆时针旋转我的船头45度， 现在我的船头朝向哪里？
某高手也许会用三角函数去解出这道题目，但这里我们会选用一种更简便的方法：我的船正处于3+4i 方向（不必在意角度到底是多少），需要正传45度。好，45度角的复数形式是 1+ i ,用它乘以原来的方向就行啦！
解题思想是这样的：
原方向：向东3个单位，向北4个单位=3 + 4i
逆时针旋转45度= 乘以 1+i
两个复数相乘得到：
所以新的船头方向是向西1个单位（向东-1个单位），向北7个单位。
惊讶吧，我们用了十秒钟就算出来的，甚至不用正弦余弦运算，也不用考虑向量、矩阵、象限等概念。仅仅使用了算数中的交叉相乘。虚数天生适合表达旋转。
计算的结果也十分有用，我们得到一个方向（-1，7），而不是一个角度（atan(7/-1),第二象限）这个角度和难用量角器画出来，却可以用坐标轻松地表示出来。
如果你和我一样，你会觉得这个方法简直太过瘾了。如果不是，额，恐怕数学不适合你，孩子。
三角运算很有用，但是复数运算可以让丑陋的计算过程变得简单（比如计算cos(a+b)）这里只做一点简单介绍，在后面的文章中我会讲全部内容奉献给你。