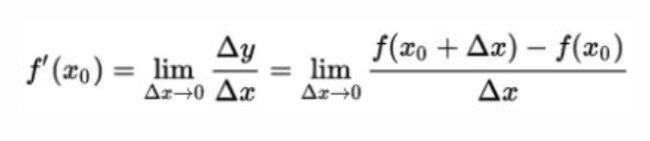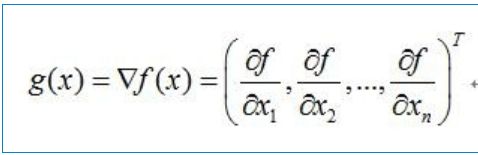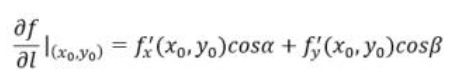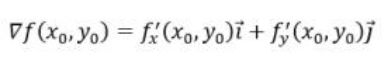微积分：
倒数和偏导数的定义
导数定义：一元导数及函数斜率，反映因变量随自变量变化的快慢
偏导数：偏导数对应多元函数的情况，对于一个 n元函数 y=f(x1,x2,…,xn)，在 ℝn 空间内的直角坐标系中，函数沿着某一条坐标轴方向的导数，就是偏导数
全微分：
若函数z = f (x, y)在点(x, y)可微分，则该函数在点(x,y)的偏导数必存在，且函数z = f (x, y)在点(x,y)的全微分为
链式求导法则：
设u=u(x)、v=v(x)在x可导，z=f(u,v)在相应点(u,v)有连续偏导数，则复合函数z=f(u(x),v(x))在x可导，则有：
梯度向量和方向导数的定义
目标函数f为单变量，是关于自变量向量x=(x1,x2,…,xn)T的函数，
单变量函数f对向量x求梯度，结果为一个与向量x同维度的向量，称之为梯度向量；
方向导数：函数在任意方向上的导数就是方向导数。
当α=0，方向I与梯度相同，增长最快；
当α=π，方向I与梯度相反，减少最快；
当α=π/2，方向I与梯度垂直，增长率为0；
方向导数和梯度的关系：
方向导数是标量，只有大小，没有方向。当函数f(x, y)在点P(x0, y0)可微时，存在如下关系式：
梯度是矢量，既有大小，又有方向，且梯度前提是函数f(x, y)具有连续一阶可偏导：
方向导数最大的方向，为梯度方向，最大方向导数是梯度的模。
方向导数最小的方向，为梯度方向的反方向，最小方向导数是梯度的模的相反数。
梯度、全微分和方向导数区别：
极值定理
当函数f(x)在闭区间[a,b]上是连续函数时，存在c属于[a,b]，d属于[a,b],有f(c)≤f(x)≤f(d),x∈[a,b]成立。
雅克比矩阵
在向量微积分中，雅可比矩阵是一阶偏导数以一定方式排列成的矩阵，其行列式称为雅可比行列式。雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近。
是在这点的导数。在此情况下，
Hession矩阵
在数学中，海赛矩阵是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵，此函数如下：
如果f所有的二阶导数都存在，那么f 的海赛矩阵即：
- H(f)ij(x) = DiDjf(x)
在x0点上，hessian矩阵是负定的，且各分量的一阶偏导数为0，则x0为极大值点。
在x0点上，hessian矩阵式正定的，且各分量的一阶偏导数为0，则x0为极小值点。
矩阵是负定的充要条件是各个特征值均为负数。
矩阵是正定的充要条件是各个特征值均为正数。
特征值：
设 A 是n阶方阵，如果存在数m和非零n维列向量 x，使得 Ax=mx 成立，则称 m 是A的一个特征值（characteristic value)或本征值（eigenvalue)。
凸函数的定义与判断方法
定义：对于D中任意两点的连线，必须在此集合内。
函数定义：
泰勒展开式
若函数f（x）在包含x0的某个闭区间[a,b]上具有n阶导数，且在开区间（a,b）上具有（n+1）阶导数，则对闭区间[a,b]上任意一点x，成立下式：
拉格朗日乘数法
拉格朗日乘子法主要用于解决约束优化问题，它的基本思想就是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有（n+k）个变量的无约束优化问题。
KKT条件：
对于不等式约束，只要满足一定的条件，依然可以使用拉格朗日乘子法解决，这里的条件便是 KKT 条件
KKT条件
对于不等式约束，只要满足一定的条件，依然可以使用拉格朗日乘子法解决，这里的条件便是 KKT 条件