C#红黑树实现代码
在学习红黑树之前,最好已经学习过AVL树了,因为二者的实现方式是有很大程度类似的(左旋和右旋),但是只不过二叉平衡树是在每次加入节点时,需要计算该节点的左右子树高度差,如果高度差大于一则旋转调节使其平衡;而红黑树是在每次加入节点时计算红黑节点之间的关系,如果关系错误,则通过旋转和改变颜色来调节树的结构。
总之,AVL树也好,RB树也好,都只不过是一种优化二叉查找树的高级方式而已。
下面是C#实现的红黑树插入操作,并附加了详细的注释,如果你了解红黑树的原理,应该很容易看懂,最后通过优雅的层序遍历将节点值和节点颜色输出出来。并且利用一个国外一个有名的红黑树网站生成了树的结构,验证了代码的正确性。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace RBTree
{
class Program
{
static void Main(string[] args)
{
int[] a = { 11, 2, 14, 1, 7, 15, 5, 8 };
RBTree rbTree = new RBTree();
foreach (var item in a)
{
rbTree.Insert(item);
}
rbTree.LayerOrder(rbTree.rootnode);
rbTree.Insert(4);
Console.WriteLine();
Console.WriteLine();
rbTree.LayerOrder(rbTree.rootnode);
Console.WriteLine();
Console.WriteLine();
}
}
public enum Color
{
red,black
}
class RBTreeNode
{
public int key;
public RBTreeNode left;
public RBTreeNode right;
public Color color;
//由于红黑树需要寻找父节点和祖父节点以及叔节点
//因而需要多设置一个parent节点来方便操作
public RBTreeNode parent;
public RBTreeNode(int item,Color color)
{
key = item;
left = null;
right = null;
this.color = color;
}
public override string ToString()
{
//重写tostring()方法,在输出时会默认调用
return key + "(" + color.ToString() + ")";
}
}
class RBTree
{
//定义根节点
public RBTreeNode rootnode;
public void Insert(int item)
{
if(rootnode == null)
{
//注意,根节点为黑色
rootnode = new RBTreeNode(item,Color.black);
}
else
{
//这一步只完成插入操作,与二叉查找的插入是一样的
var newnode = Inserts(item);
//重点在于这一步,看节点是否需要调整
InsertFixUp(newnode);
}
}
public RBTreeNode Inserts(int item)
{
var node = rootnode;
var newnode = new RBTreeNode(item,Color.red);
while (true)
{
if(item > node.key)
{
if(node.right == null)
{
//注意父子关系要确定
newnode.parent = node;
node.right = newnode;
break;
}
node = node.right;
}
else if(item < node.key)
{
if(node.left == null)
{
newnode.parent = node;
node.left = newnode;
break;
}
node = node.left;
}
}
return newnode;
}
//红黑树的关键操作,如何平衡红黑树
//插入节点的初始颜色为红,如果父节点为黑则不要平衡操作,除此之外,
//红黑树插入节点的情况可以分为一下两种:
//1.叔节点为红:祖父,父叔,当前节点,三者关系为“黑红红”改为“红黑红”即可,但是调整后的祖父节点可能不平衡,再对祖父节点进行InsertFixUp递归
//2.叔节点为黑或者为空:此时需要旋转,具体左旋还是右旋需要根据当前节点在父节点的左子树还是右子树来确定
public void InsertFixUp(RBTreeNode node)
{
var parentnode = node.parent;
//显然插入节点的父节点存在且为红我们才需要平衡操作
if (parentnode != null && parentnode.color == Color.red)
{
var gparent = parentnode.parent;
//如果父节点是祖父节点的左子节点
if(parentnode == gparent.left)
{
var unclenode = gparent.right;
//第一种情况:
//树节点存在且为红色,只需要修改颜色,然后对祖父节点递归
if(unclenode != null && unclenode.color == Color.red)
{
setRed(gparent);
setBlack(parentnode);
setBlack(unclenode);
InsertFixUp(gparent);
}
//第二种情况:
//如果叔节点为红或者不存在,那么就是分为左旋还是右旋
else
{
//类似于AVL树中的LL型,因而右旋
if(node == parentnode.left)
{
setBlack(parentnode);
setRed(gparent);
Rightrotate(gparent);
}
//类似AVL树中的LR型,先对父节点左旋
//再把父节点当做新插入的节点,进行递归
else if(node == parentnode.right)
{
LeftRotate(parentnode);
InsertFixUp(parentnode);
}
}
}
else
{
//如果父节点是祖父节点的右子节点
//与上面完全类似
var unclenode = gparent.left;
if(unclenode != null && unclenode.color == Color.red)
{
setBlack(parentnode);
setBlack(unclenode);
setRed(gparent);
InsertFixUp(gparent);
}
else
{
if(node == parentnode.right)
{
setBlack(parentnode);
setRed(gparent);
LeftRotate(gparent);
}
else if(node == parentnode.left)
{
Rightrotate(parentnode);
InsertFixUp(parentnode);
}
}
}
}
//最后将输出的根节点直接设置为黑色
setBlack(rootnode);
}
private void LeftRotate(RBTreeNode node)
{
//这里的旋转操作比AVL树复杂,因为需要交换父子节点之间的关系
//注意这里的交换顺序
var temp = node.right;
node.right = temp.left;
if(temp.left != null)
{
temp.left.parent = node;
}
temp.parent = node.parent;
if(node.parent == null)
{
rootnode = temp;
}
else
{
if(node == node.parent.left)
{
node.parent.left = temp;
}
else
{
node.parent.right = temp;
}
}
temp.left = node;
node.parent = temp;
}
private void Rightrotate(RBTreeNode node)
{
var temp = node.left;
node.left = temp.right;
//1.调整node右子节点的父节点
if(temp.right != null)
{
temp.right.parent = node;
}
//2.调整temp节点当前的父节点
temp.parent = node.parent;
//3.如果node的父节点不存在,则需要修改根节点
if(node.parent == null)
{
rootnode = temp;
}
else
{
//4.如果node的父节点存在,那么需要把temp节点分配到该父节点对应的位置
if(node == node.parent.left)
{
node.parent.left = temp;
}
else if(node == node.parent.right)
{
node.parent.right = temp;
}
}
temp.right = node;
//5.把temp节点设置为node节点的父节点
node.parent = temp;
//以上五个步骤,是与AVL树的旋转有区别的地方,其原因是为每一个node增加了parent字段,
//因而不仅需要修改节点的左右关系,还需要修改各个节点的父子关系
}
public void setBlack(RBTreeNode node)
{
node.color = Color.black;
}
public void setRed(RBTreeNode node)
{
node.color = Color.red;
}
public void LayerOrder(RBTreeNode rootnode)
{
//优雅的层序遍历
RBTreeNode current = rootnode;
Queue queue = new Queue();
queue.Enqueue(rootnode);
while (queue.Any())
{
var temp = queue.Dequeue();
//这里默认会调用tostring()方法
Console.Write(temp + " ");
if(temp.left != null)
{
queue.Enqueue(temp.left);
}
if(temp.right != null)
{
queue.Enqueue(temp.right);
}
}
}
}
}
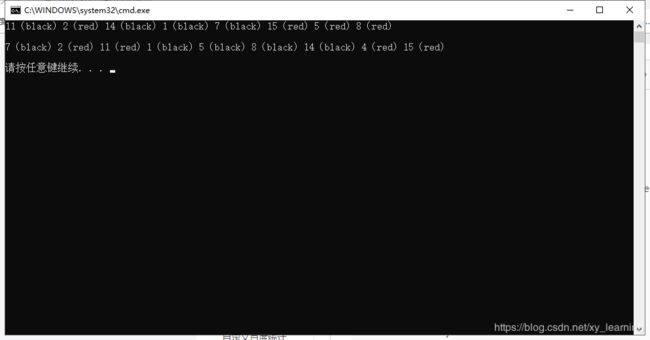
最后输出的结果:
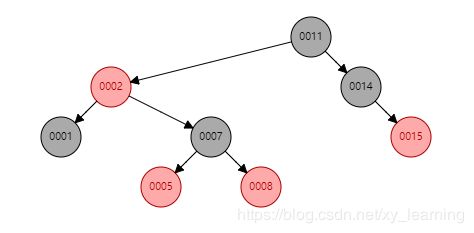
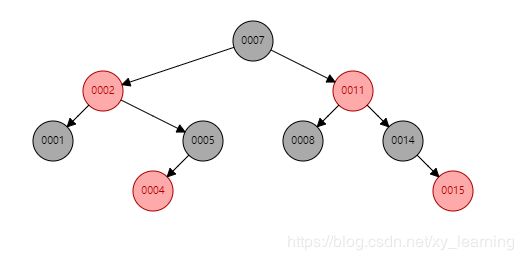
红黑树生成网站:https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
生成结果与上述结果相同,说明了代码的正确性。
参考1: https://www.jianshu.com/p/e136ec79235c
参考2:https://www.cnblogs.com/bbvi/p/5070560.html