线性判别分析(LDA)和python实现（二分类问题）
线性判别分析（Linear Discriminant Analysis, LDA）是一种经典的线性学习方法，思路是将两种数据投影到一条直线上，使这两种数据之间尽可能远离，且同类数据尽可能聚集在一起
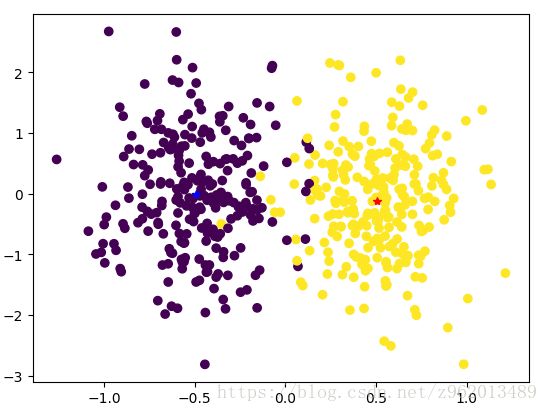
假如我们有如上图所示的2种数据集
$$X1=\left \{ x_{1}^{1}, x_{2}^{1},..., x_{n}^{1}\right \}$$
$$X2=\left \{ x_{1}^{2}, x_{2}^{2},..., x_{n}^{2}\right \}$$
其中
以及其对应的标签
我们希望有一条直线
$$y=w_{1}x_{1}+w_{2}x_{2}=\mathbf{wx}$$
使得将两种数据集中的样本带入后可以获得比较明显的分类效果，例如将X1数据集中的样本带入函数后y的值范围在[-1,0],而将X2数据集中的样本带入函数后y的值范围在[1,2]，这样就可以很轻松的进行分类了。
那么为了达到这样的效果，我们首先要让同类的样本投影点尽可能小,即期望投影后同类样本数据方差
小，然后我们还要让两个类的中心
投影后的距离尽量大，即
要尽量大。
定义“类内散度矩阵”
$$S_{w}=\Sigma _{1}+\Sigma _{2}=\sum_{x \in X1}(x-\mu_{1} )(x-\mu_{1} )^{T}+\sum_{x \in X2}(x-\mu_{2} )(x-\mu_{2} )^{T}$$
定义“类间散度矩阵”
$$S_{b}=(\mu_{1}-\mu_{2} )(\mu_{1}-\mu_{2} )^{T}$$
则我们的代价函数可写为：
$$J=\frac{w^{T}S_{b}w}{w^{T}S_{w}w} （1）$$
我们希望最大化上述代价函数，由于代价函数的分子分母都有2个w，因此J的最大解与w的长度无关，只与方向有关，我们令
$$w^{T}S_{w}w=1$$
则（1）式等价于
$$min_{w}-w^{T}S_{b}w$$
$$s.t. w^{T}S_{w}w=1$$
加入拉格朗日乘子并求导求得下式：
$$c(w)=w^{T}S_{b}w-\lambda (w^{T}S_{w}w-1)$$
$$\Rightarrow \frac{dc}{dw}=2S_{b}w-2\lambda S_{w}w=0$$
$$\Rightarrow S_{b}w=\lambda S_{w}w (2)$$
由于
的方向恒为
可以令
$$S_{b}w=\lambda (\mu_{1}-\mu_{2}) $$
带入（2）式可得
$$w=S_{w}^{-1}(\mu _{1}-\mu _{2})$$
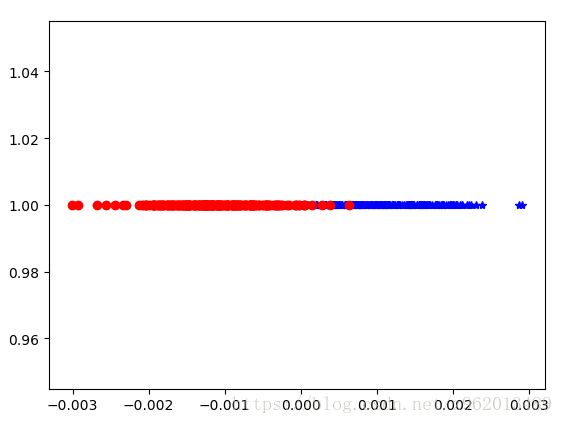
将开始时的数据使用LDA方法分类后如下图所示
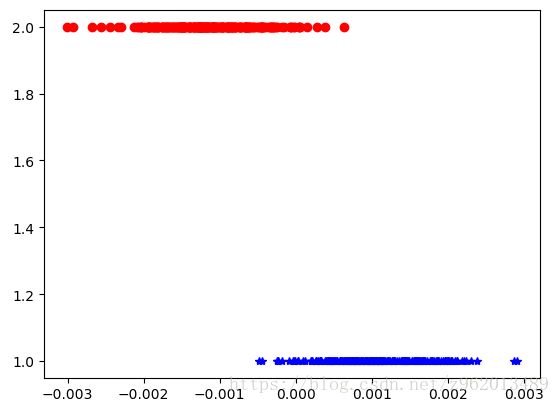
图中的点的横坐标为y值，为了观察方便，我们将各点的纵坐标设为其标签，获得下图
python3.6实现如下：
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_classification
from mpl_toolkits.mplot3d import Axes3D
def LDA(X, y):
X1 = np.array([X[i] for i in range(len(X)) if y[i] == 0])
X2 = np.array([X[i] for i in range(len(X)) if y[i] == 1])
len1 = len(X1)
len2 = len(X2)
mju1 = np.mean(X1, axis=0)#求中心点
mju2 = np.mean(X2, axis=0)
cov1 = np.dot((X1 - mju1).T, (X1 - mju1))
cov2 = np.dot((X2 - mju2).T, (X2 - mju2))
Sw = cov1 + cov2
w = np.dot(np.mat(Sw).I, (mju1 - mju2).reshape((len(mju1), 1))) # 计算w
X1_new = func(X1, w)
X2_new = func(X2, w)
y1_new = [1 for i in range(len1)]
y2_new = [2 for i in range(len2)]
return X1_new, X2_new, y1_new, y2_new
def func(x, w):
return np.dot((x), w)
if '__main__' == __name__:
X, y = make_classification(n_samples=500, n_features=2, n_redundant=0, n_classes=2,
n_informative=1, n_clusters_per_class=1, class_sep=0.5, random_state=10)
X1_new, X2_new, y1_new, y2_new = LDA(X, y)
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)
plt.show()
plt.plot(X1_new, y1_new, 'b*')
plt.plot(X2_new, y2_new, 'ro')
plt.show()参考：
https://blog.csdn.net/u012005313/article/details/50933517
https://www.cnblogs.com/engineerLF/p/5393119.html
《机器学习》周志华
注：numpy中array类型的二维矩阵A求逆若使用A**(-1)求出来不是逆矩阵，也不知道求出来的是什么，之前写程序就被这个东西坑了
下一篇博客介绍了对多分类问题的降维处理
https://blog.csdn.net/z962013489/article/details/79918758