高博14讲--第七讲 视觉里程计-7.3 2D-2D:对极几何(未完待续)
高博14讲--第七讲 视觉里程计-7.3 2D-2D:对极几何
- 基本问题
- 对极约束
- 对极约束推导过程
- 本质矩阵
- 八点法
- 八点法推导过程
- 本质矩阵$\ E$的SVD分解
- 八点法的讨论
- 合理的创建标题,有助于目录的生成
- 如何改变文本的样式
- 插入链接与图片
- 如何插入一段漂亮的代码片
- 生成一个适合你的列表
- 创建一个表格
- 设定内容居中、居左、居右
- SmartyPants
- 创建一个自定义列表
- 如何创建一个注脚
- 注释也是必不可少的
- KaTeX数学公式
- 新的甘特图功能,丰富你的文章
- UML 图表
- FLowchart流程图
- 导出与导入
- 导出
- 导入
基本问题
当相机为单目时,只知道2D的像素坐标,根据两组2D点估计相机的运动,用对极几何来解决。
对极约束
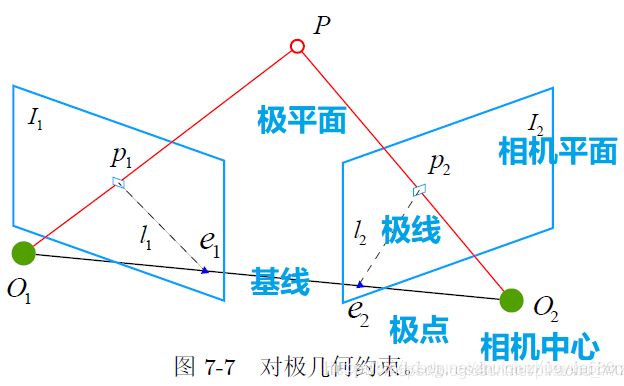
两个相机之间的变换为 T 12 \ T_{12} T12: p 1 = T 12 ⋅ p 2 \ p_1=T_{12}·p_2 p1=T12⋅p2,即:通过 P 2 \ P_2 P2的坐标乘以 T 12 \ T_{12} T12,即可求得 P 1 \ P_1 P1的坐标 。
在实践中:
- 已知:匹配点对 p 1 \ p_1 p1, p 2 \ p_2 p2的像素坐标。
- 给定:两张二维图像,二维图像上特征点的匹配关系。
- 未知:P的三维空间坐标, I 1 \ I_1 I1到I I 2 \ I_2 I2的变换矩阵( T 1 , 2 \ T_{1,2} T1,2, 即 R , T \ {R,T} R,T)。
- 一般是用于单目SLAM的初始化,用对极几何可求出位姿,在用三角测量估计三维空间点的位置后,就能用其他更准确的方法继续求解了。
对极约束推导过程
设P在图1的相机坐标系下,坐标为: P = [ X , Y , Z ] T P=[X,Y,Z]^T P=[X,Y,Z]T
p 1 \ p_1 p1, p 2 \ p_2 p2的像素坐标(单位像素): s 1 p 1 = K P , s 2 p 2 = K ( R P + t ) s_1p_1=KP,s_2p_2=K(RP+t) s1p1=KP,s2p2=K(RP+t)
K \ K K为相机的内参矩阵, R , t \ R,t R,t为两个坐标系的相机运动。
使用齐次坐标,上式乘以非零常数都成立: p 1 = K P , p 2 = K ( R P + t ) p_1=KP,p_2=K(RP+t) p1=KP,p2=K(RP+t)
其归一化平面坐标(单位米): x 1 = K − 1 p 1 , x 2 = K − 1 p 2 x_1=K^{-1}p_1,x_2=K^{-1}p_2 x1=K−1p1,x2=K−1p2
得到: x 2 = R x 1 + t x_2=Rx_1+t x2=Rx1+t
这里的 x 1 , x 2 \ x_1,x_2 x1,x2是齐次坐标,等式表达了一个齐次关系。
两边同时左乘 t \ t t^,即:两侧同时与 t \ t t做外积,即,与 t \ t t作叉乘: t × x 2 = t × R x 1 + t × t t×x_2=t×Rx_1+t×t t×x2=t×Rx1+t×t
t \ t t与 t \ t t作叉乘,夹角为0,则结果为0,即: t × t = 0 \ t×t=0 t×t=0,上式化简为: t × x 2 = t × R x 1 t×x_2=t×Rx_1 t×x2=t×Rx1
两侧同时左乘 x 2 T \ x_2^T x2T: x 2 T t × x 2 = x 2 T t × R x 1 x_2^Tt×x_2=x_2^Tt×Rx_1 x2Tt×x2=x2Tt×Rx1
左式中, t × x 2 \ t×x_2 t×x2是一个与 t \ t t 和 x 2 \ x_2 x2都垂直的向量,把它再和 x 2 \ x_2 x2做内积时,将得到0。
所以得到对极约束, x 1 , x 2 为 归 一 化 坐 标 \ x_1,x_2为归一化坐标 x1,x2为归一化坐标: x 2 T t × R x 1 = 0 x_2^Tt×Rx_1=0 x2Tt×Rx1=0
重新带入 p 1 , p 2 \ p_1,p_2 p1,p2, p 1 , p 2 为 像 素 坐 标 \ p_1,p_2为像素坐标 p1,p2为像素坐标: p 2 T K − T t × R K − 1 p 1 = 0 p_2^TK^{-T}t×RK^{-1}p_1=0 p2TK−Tt×RK−1p1=0
上面两式子为对极约束,几何意义是: O 1 , P , O 2 \ O_1,P,O_2 O1,P,O2三者共面。
定义本质矩阵 E \ E E(Essential Matrix)和基础矩阵 F \ F F(Fundamental Matrix): E = t × R , F = K − T E K − 1 E=t×R,F=K^{-T}EK{-1} E=t×R,F=K−TEK−1
所以对极约束简写为: x 2 T E x 1 = p 2 T F p 1 = 0 x_2^TEx_1=p_2^TFp_1=0 x2TEx1=p2TFp1=0
根据对极约束,相机位姿估计问题变为以下两步,即估计 R , t \ R,t R,t的方法为:
1.根据匹配点的位置,求出 E \ E E或者 F \ F F。
2.根据 E \ E E或者 F \ F F,求出 R , t \ R,t R,t。
本质矩阵
本质矩阵长什么样子:
· E = t × R \ E=t×R E=t×R, E \ E E是一个3×3的矩阵,内有9个未知数。
· E \ E E在不同尺度下是等价的( E \ E E具有尺度等价性):由于对极约束是等式为零的约束,所以对 E \ E E 乘以任意非零常数后,对极约束依然满足。
· 平移和旋转各有3个自由度,所以 t × R \ t×R t×R共6个自由度。由于 E \ E E具有尺度等价性,这是由于对极约束 的性质,其乘任意非零向量依然满足,即增加一个约束条件,所以6个自由度中可以去掉一个, 所以 E \ E E实际有5个自由度。
八点法
· E \ E E具有5个自由度,最少使用5对点来求解 E \ E E。但是, E \ E E具有一种非线性性质,在求解线性方程时会 很麻烦。
· 把 E \ E E当成一个3×3的普通矩阵,共9个自由度,由于 E \ E E的尺度等价性, E \ E E具有8个自由度,使用8对点 来估计 E \ E E,这就是“八点法”。
八点法推导过程
一对匹配点,它们的归一化坐标为 x 1 = [ u 1 , v 1 , 1 ] T , x 2 = [ u 2 , v 2 , 1 ] T \ x_1=[u_1,v_1,1] ^ T,x_2=[u_2,v_2,1]^T x1=[u1,v1,1]T,x2=[u2,v2,1]T,根据对极约束,有:
[ u 1 , v 1 , 1 ] [ e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ] [ u 2 v 2 1 ] = 0 [u_1,v_1,1] \left[ \begin{matrix} e_1 & e_2 & e_3 \\ e_4 & e_5 & e_6 \\ e_7 & e_8 & e_9 \end{matrix} \right] \left[ \begin{matrix} u_2 \\ v_2 \\ 1 \end{matrix} \right]=0 [u1,v1,1]⎣⎡e1e4e7e2e5e8e3e6e9⎦⎤⎣⎡u2v21⎦⎤=0
把 E \ E E展开,写成向量的形式:
e = [ e 1 , e 2 , e 3 , e 4 , e 5 , e 6 , e 7 , e 8 , e 9 ] T e=[e_1,e_2,e_3,e_4,e_5,e_6,e_7,e_8,e_9]^T e=[e1,e2,e3,e4,e5,e6,e7,e8,e9]T
把对极约束写成与 e \ e e有关的线性形式:
[ u 1 u 2 , u 1 v 2 , u 1 , v 1 u 2 , v 1 v 2 , v 1 , u 2 , v 2 , 1 ] e = 0 [u_1u_2,u_1v_2,u_1,v_1u_2,v_1v_2,v_1,u_2,v_2,1]e=0 [u1u2,u1v2,u1,v1u2,v1v2,v1,u2,v2,1]e=0
同理,对于其他店对也有相同的表示。把所有点都放在一个方程中,变成线性方程组( u i , v i \ u^i,v^i ui,vi表示第 i \ i i个特征点):
[ u 1 1 u 2 1 u 1 1 v 2 1 u 1 1 v 1 1 u 2 1 v 1 1 v 2 1 v 1 1 u 2 1 v 2 1 1 u 1 2 u 2 2 u 1 2 v 2 2 u 1 2 v 1 2 u 2 2 v 1 2 v 2 2 v 1 2 u 2 2 v 2 2 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . u 1 8 u 2 8 u 1 8 v 2 8 u 1 8 v 1 8 u 2 8 v 1 8 v 2 8 v 1 8 u 2 8 v 2 8 1 ] [ e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ] = 0 \left[ \begin{matrix} {u_1}^1{u_2}^1&{u_1}^1{v_2}^1&{u_1}^1&{v_1}^1{u_2}^1&{v_1}^1{v_2}^1&{v_1}^1&{u_2}^1&{v_2}^1&1\\ {u_1}^2{u_2}^2&{u_1}^2{v_2}^2&{u_1}^2&{v_1}^2{u_2}^2&{v_1}^2{v_2}^2&{v_1}^2&{u_2}^2&{v_2}^2&1 \\ ...&...&...&...&...&...&...&...&...\\ {u_1}^8{u_2}^8&{u_1}^8{v_2}^8&{u_1}^8&{v_1}^8{u_2}^8&{v_1}^8{v_2}^8&{v_1}^8&{u_2}^8&{v_2}^8&1 \end{matrix} \right]\left[ \begin{matrix} e_1 \\ e_2 \\ e_3 \\ e_4 \\ e_5 \\ e_6 \\ e_7 \\ e_8 \\ e_9 \end{matrix} \right]=0 ⎣⎢⎢⎡u11u21u12u22...u18u28u11v21u12v22...u18v28u11u12...u18v11u21v12u22...v18u28v11v21v12v22...v18v28v11v12...v18u21u22...u28v21v22...v2811...1⎦⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡e1e2e3e4e5e6e7e8e9⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤=0
由上式可以求得 E \ E E,根据 E \ E E求取相机的运动 R , t \ R,t R,t。
本质矩阵 E \ E E的SVD分解
根据 E \ E E求取相机的运动 R , t \ R,t R,t,对 E \ E E进行奇异值分解( S V D \ SVD SVD):
设 E \ E E的SVD分解为:
E = U Σ V T E=U\Sigma{V^T} E=UΣVT
其中 U , V \ U,V U,V为正交阵, Σ \ \Sigma Σ为奇异值矩阵。根据本质矩阵 E \ E E的内在性质, E \ E E的奇异值必定为 [ σ , σ , 0 ] T \ [\sigma,\sigma,0]^T [σ,σ,0]T, 所以 Σ = d i a g [ σ , σ , 0 ] \ \Sigma=diag[\sigma,\sigma,0] Σ=diag[σ,σ,0]
在 S V D \ SVD SVD分解中,对于任意一个 E \ E E,存在两个可能的 t , R \ t,R t,R与它对应:
t 1 Λ = U R Z ( π 2 ) Σ U T , R 1 = U R Z T ( π 2 ) V T t_1^{\Lambda}=UR_Z(\frac{π}{2}){\Sigma}U^T,R_1=UR_Z^T(\frac{π}{2})V^T t1Λ=URZ(2π)ΣUT,R1=URZT(2π)VT
t 2 Λ = U R Z ( − π 2 ) Σ U T , R 2 = U R Z T ( − π 2 ) V T t_2^{\Lambda}=UR_Z(-\frac{π}{2}){\Sigma}U^T,R_2=UR_Z^T(-\frac{π}{2})V^T t2Λ=URZ(−2π)ΣUT,R2=URZT(−2π)VT
其中 R Z T ( π 2 ) \ R_Z^T(\frac{π}{2}) RZT(2π)表示沿 Z \ Z Z轴旋转 9 0 ∘ \ 90^\circ 90∘得到的旋转矩阵。
由于 − E \ -E −E和 E \ E E等价,所以任意一个 t \ t t取负号,也会得到相同的结果。因此,从 E \ E E分解到 t , R \ t,R t,R时,一共存在4个可能的解。
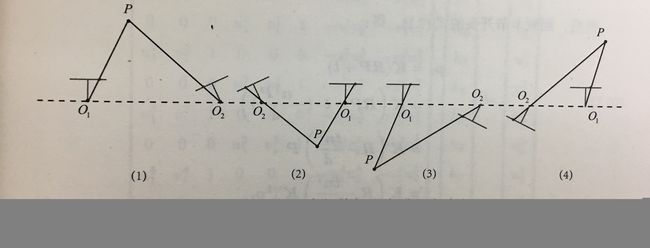 (1) P \ P P在 O 1 , O 2 \ O_1,O_2 O1,O2两个相机的前面,深度都为正。
(1) P \ P P在 O 1 , O 2 \ O_1,O_2 O1,O2两个相机的前面,深度都为正。
(2) P \ P P在 O 1 , O 2 \ O_1,O_2 O1,O2两个相机的后面,深度都为负。
(3) P \ P P在 O 1 \ O_1 O1相机的后面,深度为负;在 O 2 \ O_2 O2相机的前面,深度为正。
(4) P \ P P在 O 1 \ O_1 O1相机的前面,深度为正;在 O 2 \ O_2 O2相机的后面,深度为负。
假设一共有N个特征点,则列出如下线性方程组:
八点法的讨论
(1)用于单目SLAM的初始化
一开始,相机在运动时,只知道图像与图像之间的关系,只知道第一帧图像的特征点与第二帧图像的特征点之间的匹配关系,只能得到 2 D − 2 D \ 2D-2D 2D−2D之间的关系。
当初始化之后,可以得到 3 D \ 3D 3D的点。当知道这两帧图像之间相机的运动,并计算出图像中点的深度值,这样就有 3 D \ 3D 3D的点,之后使用 3 D − 2 D \ 3D-2D 3D−2D的 P n P \ PnP PnP算法求解。
(2)尺度不确定性:归一化或特征点的平均深度
一开始,
当初始化之后,
撤销:Ctrl/Command + Z
重做:Ctrl/Command + Y
加粗:Ctrl/Command + B
斜体:Ctrl/Command + I
标题:Ctrl/Command + Shift + H
无序列表:Ctrl/Command + Shift + U
有序列表:Ctrl/Command + Shift + O
检查列表:Ctrl/Command + Shift + C
插入代码:Ctrl/Command + Shift + K
插入链接:Ctrl/Command + Shift + L
插入图片:Ctrl/Command + Shift + G
合理的创建标题,有助于目录的生成
直接输入1次#,并按下space后,将生成1级标题。
输入2次#,并按下space后,将生成2级标题。
以此类推,我们支持6级标题。有助于使用TOC语法后生成一个完美的目录。
如何改变文本的样式
强调文本 强调文本
加粗文本 加粗文本
标记文本
删除文本
引用文本
H2O is是液体。
210 运算结果是 1024.
插入链接与图片
链接: link.
图片: ![]()
带尺寸的图片: ![]()
居中的图片: ![]()
居中并且带尺寸的图片: ![]()
当然,我们为了让用户更加便捷,我们增加了图片拖拽功能。
如何插入一段漂亮的代码片
去博客设置页面,选择一款你喜欢的代码片高亮样式,下面展示同样高亮的 代码片.
// An highlighted block
var foo = 'bar';
生成一个适合你的列表
- 项目
- 项目
- 项目
- 项目
- 项目1
- 项目2
- 项目3
- 计划任务
- 完成任务
创建一个表格
一个简单的表格是这么创建的:
| 项目 | Value |
|---|---|
| 电脑 | $1600 |
| 手机 | $12 |
| 导管 | $1 |
设定内容居中、居左、居右
使用:---------:居中
使用:----------居左
使用----------:居右
| 第一列 | 第二列 | 第三列 |
|---|---|---|
| 第一列文本居中 | 第二列文本居右 | 第三列文本居左 |
SmartyPants
SmartyPants将ASCII标点字符转换为“智能”印刷标点HTML实体。例如:
| TYPE | ASCII | HTML |
|---|---|---|
| Single backticks | 'Isn't this fun?' |
‘Isn’t this fun?’ |
| Quotes | "Isn't this fun?" |
“Isn’t this fun?” |
| Dashes | -- is en-dash, --- is em-dash |
– is en-dash, — is em-dash |
创建一个自定义列表
- Markdown
- Text-to- HTML conversion tool
- Authors
- John
- Luke
如何创建一个注脚
一个具有注脚的文本。1
注释也是必不可少的
Markdown将文本转换为 HTML。
KaTeX数学公式
您可以使用渲染LaTeX数学表达式 KaTeX:
Gamma公式展示 Γ ( n ) = ( n − 1 ) ! ∀ n ∈ N \Gamma(n) = (n-1)!\quad\forall n\in\mathbb N Γ(n)=(n−1)!∀n∈N 是通过欧拉积分
Γ ( z ) = ∫ 0 ∞ t z − 1 e − t d t . \Gamma(z) = \int_0^\infty t^{z-1}e^{-t}dt\,. Γ(z)=∫0∞tz−1e−tdt.
你可以找到更多关于的信息 LaTeX 数学表达式here.
新的甘特图功能,丰富你的文章
- 关于 甘特图 语法,参考 这儿,
UML 图表
可以使用UML图表进行渲染。 Mermaid. 例如下面产生的一个序列图::
这将产生一个流程图。:
- 关于 Mermaid 语法,参考 这儿,
FLowchart流程图
我们依旧会支持flowchart的流程图:
- 关于 Flowchart流程图 语法,参考 这儿.
导出与导入
导出
如果你想尝试使用此编辑器, 你可以在此篇文章任意编辑。当你完成了一篇文章的写作, 在上方工具栏找到 文章导出 ,生成一个.md文件或者.html文件进行本地保存。
导入
如果你想加载一篇你写过的.md文件或者.html文件,在上方工具栏可以选择导入功能进行对应扩展名的文件导入,
继续你的创作。
注脚的解释 ↩︎