NaiveBayes Class

NavieBayes Class(朴素贝叶斯分类器)

贝叶斯定理

贝叶斯定理解决了现实生活里经常遇到的问题：已知某条件概率，如何得到两个事件交换后的概率，也就是在已知P(A|B)的情况下如何求得P(B|A)。这里先解释什么是条件概率：
P(A|B)表示事件B已经发生的前提下，事件A发生的概率，叫做事件B发生下事件A的条件概率。其基本求解公式为：

P(A|B)=P(AB)P(B)

贝叶斯定理之所以有用，是因为我们在生活中经常遇到这种情况：我们可以很容易直接得出P(A|B)，P(B|A)则很难直接得出，但我们更关心P(B|A)，贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。
下面不加证明地直接给出贝叶斯定理：

P(B|A)=P(AB)P(A)

朴素贝叶斯分类的原理与流程

朴素贝叶斯分类是一种十分简单的分类算法，叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素。
朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。
通俗来说，就好比这么个道理，你在街上看到一个黑人，我问你你猜这哥们哪里来的，你十有八九猜非洲。为什么呢？因为黑人中非洲人的比率最高，当然人家也可能是美洲人或亚洲人，但在没有其它可用信息下，我们会选择条件概率最大的类别，这就是朴素贝叶斯的思想基础。
朴素贝叶斯分类器应用的学习任务中，每个实例x可由属性值的合取描述，而目标函数f(x)从某有限集合V中取值。学习器被提供一系列关于目标函数的训练样例，以及新实例（描述为属性值的元组） < a1,a2…an > ，然后要求预测新实例的目标值（或分类）。
贝叶斯方法的新实例分类目标是在给定描述实例的属性值 < a1,a2…an > 下, 得到最可能的目标值 VMAP 。

VMAP=argmaxvj∈VP(vj|a1,a2,..,an)

可使用贝叶斯公式将此表达式重写为

VMAP =argmaxvj∈VP(a1,a2,...,an|vj)P(vj)P(a1,a2,...,an)=argmaxvj∈VP(a1,a2,...,an|vj)P(vj)

现在要做的是基于训练数据估计两个数据项的值。估计每个P(vj)很容易，只要计算每个目标值vj出现在训练数据中的频率就可以。然而，除非有一非常大的训练数据的集合，否则用这样方法估计不同的 P(a1,a2…an|vj) 项不太可行。问题在于这些项的数量等于可能实例的数量乘以可能目标值的数量。因此为获得合理的估计，实例空间中每个实例必须出现多次。
朴素贝叶斯分类器基于一个简单的假定：在给定目标值时属性值之间相互条件独立。换言之，该假定说明给定实例的目标值情况下，观察到联合的 a1,a2…an 的概率正好是对每个单独属性的概率乘积：

P(a1,a2,..,an|vj)=∏iP(ai|vj)

简化后，可以得到朴素贝叶斯分类器所使用的方法：

朴素贝叶斯分类器:

VNB=argmaxvj∈VP(vj)∏iP(ai|vj)

其中 vNB 表示朴素贝叶斯分类器输出的目标值。注意在朴素贝叶斯分类器中，须从训练数据中估计的不同 P(ai|vj) 项的数量——这比要估计P(a1,a2…an|vj)项所需的量小得多。
概括地讲，朴素贝叶斯学习方法需要基于它们在训练数据上的频率,估计不同的 P(vj) 和 P(ai|vj) 项。这些估计对应了待学习的假设。然后该假设使用上面式中的规则来分类新实例。只要所需的条件独立性能够被满足，朴素贝叶斯分类 vNB 等于MAP分类。朴素贝叶斯学习方法和其他已介绍的学习方法之间有一有趣的差别：没有明确的搜索假设空间的过程（这里，可能假设的空间为可被赋予不同的P(vj)和P(ai|vj)项的可能值。相反，假设的形成不需要搜索，只是简单地计算训练样例中不同数据组合的出现频率）。

朴素贝叶斯分类的正式定义

1. 设x= a1,a2,...,am 为一个待分类项，而每个 ai 为x的一个特征属性;
2. 有类别集合 C=y1,y2,...,yn ;
3. 计算 P(y1|x),P(y2|x),...,P(yn|x) ;
4. 如果 P(yk|x)=maxP(y1|x),P(y2|x),...,P(yn|x) , 则 x∈yk 。
   那么现在的关键就是如何计算第3步中的各个后验概率。我们可以这么做：
   1> 找到一个已知分类的待分类项集合，这个集合叫做训练样本集。
   2> 统计得到在各类别下各个特征属性的条件概率估计, 即:
   P(a1|y1),P(a2|y1),...,P(am|y1) ;
   ⋅⋅⋅⋅⋅⋅
   P(a1|yn),P(a2|yn),...,P(am|yn) .
   3> 如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：
   
   P(yi|x)=P(x|yi)P(yi)P(x)
   
   因为分母对于所有类别为常数，我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有：
   
   P(x|yi)P(yi) =P(a1|yi)P(a2|yi)...P(am|yi)P(yi)=P(yi)∏j=1mP(aj|yi)

朴素贝叶斯分类的数学定义

已知集合： C=y1,y2,...,yn 和 I=x1,x2,...,xm,... ，确定映射规则 y=f(x) , 使得任意 xi∈I 有且仅有一个 yi∈C 使得 yi=f(xi) 成立。
其中C叫做类别集合，其中每一个元素是一个类别，而I叫做项集合，其中每一个元素是一个待分类项，f叫做分类器。分类算法的任务就是构造分类器f。
这里要着重强调，分类问题往往采用经验性方法构造映射规则，即一般情况下的分类问题缺少足够的信息来构造100%正确的映射规则，而是通过对经验数据的学习从而实现一定概率意义上正确的分类，因此所训练出的分类器并不是一定能将每个待分类项准确映射到其分类，分类器的质量与分类器构造方法、待分类数据的特性以及训练样本数量等诸多因素有关。

朴素贝叶斯分类器训练方法

以matlab为例
matlab中的贝叶斯分类器(NaiveBayes class)
matlab 2016b —> NaiveBayes class(后续版本将会删除)

Description

A NaiveBayes object defines a Naive Bayes classifier. A Naive Bayes classifier assigns a new observation to the most probable class, assuming the features are conditionally independent given the class value.
假设特征独立的情况下，构造一个贝叶斯分类器；

Construction

NaivesBayes： 构造NaiveBayes类

Methods

disp:  Display NaiveBayes classifier object；
display:  Display NaiveBayes classifier object;
fit:  通过训练数据构造一个NaiveBayes类；
posterior:  计算测试数据下每个类的后验概率；
predict:  预测测试数据的类标签；
subsasgn:  Subscripted reference for NaiveBayes object
subsref:  Subscripted reference for NaiveBayes object

Properties

ClsNonEmpty:  非空类的标签
ClassLevels： 统计数据中的类型(Class levels)
Dist: 特征分布的名字(Distribution names)
        'normal'    正态分布(Normal distribution)
        'kernel'    平滑核密度估计(kernel smoothing density estimate)
        'mvmn'      多元多项分布(Multivariate multinominal distribution)
        'mn'        Multinomial bag-of-tokens model
NClasses:  类别数目(Number of classes)
NDims:  特征维度(Number of dimensions)
Params:  评估的参数(Parameter estimates)
    属性参数是一个 NClass x NDims 的元胞数组(元胞内的每一个元素为一个数组)，它包含了除类先验属性之外的参数信息，Params（i，j）表示第i个类下第j个特征的评估参数。
        'normal'  一个二维的向量，向量中第一个元素表示正态分布均值，第二个元素表示标准差；
        'kernel'  一个 ProbDistUnivKernel 类
        'mvmn'    表示i类下第j个特征可能服从的分布的概率(如高斯混合模型)
        'mn'      A scalar representing the probability the jth token appearing in the ith class, Prob(token j | class i). It is estimated as (1 + the number of occurrence of token J in class I)/(NDims + the total number of token occurrence in class I).
Prior:  类先验(Class priors), 是一个长度为NClasses的向量，包含了每一个类才样本中出现的概率

以下是matlab自带的example
1. 考虑正态分布情况(‘normal’)
首先加载一个费舍尔数据样本

    load fisheriris
    X = meas(:,3:4);  %选取数据的第3和第4个特征作为训练特征；
    Y = species;  % Y是分类标签
    tabulate(Y);  % 用表格的形式统计样本中的种类数量及其概率；
    NBModel = fitNaiveBayes(X,Y)； %以默认'normal'的形式训练出一个NaiveBayes类；
    setosaIndex = strcmp(NBModel.ClassLevels,'setosa'); %获取类setosa的参数索引； 
    estimates = NBModel.Params{setosaIndex,1} %获取第一个特征的评估参数；

画出三种类别下数据的高斯曲线；

    figure
    gscatter(X(:,1),X(:,2),Y); %画出散度图(如下图)

    h = gca; %获得坐标属性；
    xylim = [h.XLim h.YLim]; 
    hold on; %保留图表信息；
    Params = cell2mat(NBModel.Params)； % 将存储参数的原胞转换为矩阵；
    Mu = Params(2*(1:3)-1,1:2); % 获取每个参数对应的高斯均值；
    Sigma = zeros(2,2,3);
    for j = 1:3
        Sigma(:,:,j) = diag(Params(2*j,:)); % Extracts the standard deviations
        % ezcontour: 画出引用函数对应的曲线图
        % mvnpdf: 多元正态分布函数；
        % 句柄函数@(x1,x2)mvnpdf([x1,x2],Mu(j,:),Sigma(:,:,))用来表示对应的二元正态分布函数(取两个特征是为了形象表示)
        ezcontour(@(x1,x2)mvnpdf([x1,x2],Mu(j,:),Sigma(:,:,j)),...
            xylim+0.5*[-1,1,-1,1]) ...
            % Draws contours for the multivariate normal distributions
    end

用训练出的参数画出每一类对应的二元正态分布曲线图如下：

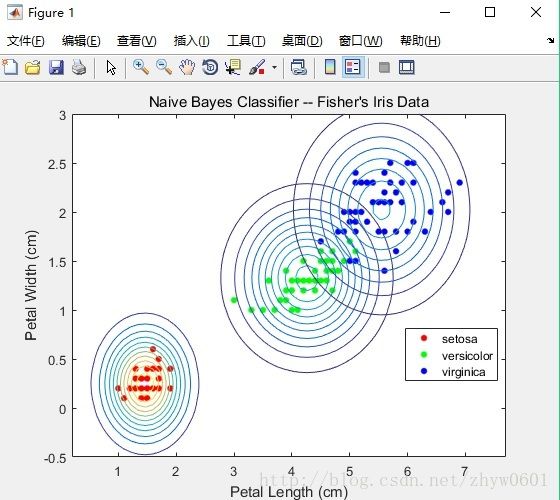
用训练出的模型进行预测

    load fisheriris
    X = meas;
    Y = species;
    NBModel1 = fitNaiveBayes(X,Y);
    NBModel1.ClassLevels % Display the class order
    NBModel1.Params
    NBModel1.Params{1,2}
    predictLabels1 = predict(NBModel1,X); %用训练出的模型对样本数据进行预测
    [ConfusionMat1,labels] = confusionmat(Y,predictLabels1) % 统计样本数据和预测结果的差别
    %Element (j, k) of ConfusionMat1 represents the number of observations that the software classifies as k, but the data show as being in class j.

1. Kernel smoothing density estimate

    NBModel2 = fitNaiveBayes(X,Y,...
    'Distribution',{'normal','kernel','normal','kernel'});
    NBModel2.Params{1,2}

我们用KDE来做1,3特征的模型，用标准正态分布来做2,4特征的模型；

3. Nayes Classifiers Using Multinomial Predictors
以垃圾分类器来做说明
假设需要对1000封邮件进行垃圾处理，我们用以下的方式来模拟，其中用-1和1来对垃圾邮件和非垃圾邮件进行标记；

n = 1000;
rng(1); % For reproducibility
y = randsample([-1 1],n true)

为了建立一个预测数据，假设词汇中有5个tokens，在每封邮件中有20个tokens作为特征。那么垃圾邮件中 tokens 出现的频率与非垃圾中出项的频率不同。

tokenProbs = [0.2 0.3 0.1 0.15 0.25;...
    0.4 0.1 0.3 0.05 0.15];             % Token relative frequencies
tokensPerEmail = 20;
X = zeros(n,5);
%% 随机生成垃圾邮件
% mnrnd生成多元随机数
%% r = mnrnd(n,p)
% 生成随机数r，r服从n和p设定的多元分布，其中，n指定每个多元分布输出的样本大小(
% 生成的r的每个元素要小于等于n);
% p是一个k维向量，P的模为1，其中的每个元素指定对应分布的概率;
% r也是一个k维行向量，它包含了n个样本中，对应k个多元概率分布的样本个数；
%% R= mnrnd(n,p,m) 生成m个 1 x k 的样本数据；
X(y==1,:) = mnrnd(tokensPerEmail,tokenProbs(1,:),sum(y==1));
X(y==-1,:) = mnrnd(tokensPerEmail,tokenProbs(2,:),sum(y==-1));
%% 训练数据
NBModel = fitNaiveBayes(X,y,'Distribution','mn');
% 验证错误率
predSpam = predict(NBModel,X);
misclass = sum(y'~=predSpam)/n

mn对应的一般是词袋模型，即每封邮件中的20个词对应的5个tokens出现的概率；

重新整理参数

Input Arguments
 X:  predictor data
 Y:  Class labels
   'kernel'     Kernel smoothing density estimate
   'mn':        Multinomial distribution. If you specify mn, then all features are components of a multinomial distribution. Therefore, you cannot include 'mn' as an element of a cell array of character vectors  
   'mvmn':      Multivariate multinomial distribution
   'normal':    Normal (Gaussian) distribution.
        'KSSupport':   Kernel smoothing density support
            'ubbounded(default)'|'positive'|cell array|mumeric row vector
            控制KDE的上下界
        'KSType':      Kernel smoother type
            'nomal(default)'|'box'|'epapnechnikov'|'triangle'|cell array of character vectors
        'KSWidth':     Kernel smoothing window bandwidth
'Prior':  Class prior probabilities
    'empirical':  uses the class relative frequencies distribution for the prior probabilities
    'numeric vector':  A numeric vector of length K specifying the prior probabilities for each class. The order of the elements of Prior should correspond to the order of the class levels
    'structure array':  A structure array S containing class levels and their prior probabilities. S must have two fields:
        S.prob: A numeric vector of prior probabilities. The software normalizes prior probabilities to sum to 1.
        S.group: A vector of the same type as Y containing unique class levels indicating the class for the corresponding element of S.prob. S.class must contain all the K levels in Y. It can also contain classes that do not appear in Y. This can be useful if X is a subset of a larger training set. The software ignores any classes that appear in S.group but not in Y.
    'uniform':  The prior probabilities are equal for all classes.
Output Arguments
'NBModel':  训练好的朴素贝叶斯分类器(Traied naive Bayes classifier)。