ANN to SNN
论文名:Conversion of Continuous-Valued Deep Networks to Efficient Event-Driven Networks for Image Classification
中文名:将连续值深度网络转换为高效的事件驱动SNN做图像分类
1. 摘要
脉冲神经网络(SNN)可能提供了一种高效的推理方法,因为网络中的神经元是稀疏激活的,并且计算是事件驱动型。之前的工作已经展示了简单的连续值CNN可以转换为精确的脉冲等价物。这些网络不包含像最大池化、softmax、batch-normalization和Inception模块这种常见的操作。本篇论文将会展示这些操作等价的脉冲操作,它几乎可以转换任意结构的CNN网络。我们展示了流行的CNN架构(包括VGG-16和Inception-v3)转换为SNN之后的最好的性能结果(在MNIST、CIFAR-10、ImageNet数据集上)。SNN在分类的错误率和操作的数量上做了一个权衡,从LeNet(MNIST)和BinaryNet(CIFAR-10)的例子来看,我们转换之后的错误率高了一点点,但是SNN的操作相比于原始的CNN减少了2倍。这凸显了SNN的潜能,尤其是当在嵌入式平台上部署高能效的脉冲神经芯片时。
2. 方法
2.1 ANN转换到SNN的理论
从ANN到SNN的转换最基本的原则就是脉冲神经元的发放频率应该和ANN里面的模拟激活值相匹配。Cao等人首次提出了一种转换ReLU层的机制,但是这个工作的理论部分很缺乏,在这里我们展示了一种近似的分析解释,并且在它的基础上提出了对脉冲发放后的reset机制提出了一个简单的修改,这使得每个SNN神经元转换成对目标函数的无偏置的近似。
我们假设在每个SNN单元和ANN单元之间存在一一映射,即使每个ANN单元对应一组脉冲神经元是有可能的。对于一个L层的网络,我们让 W l , l ∈ { 1 , 2 , . . . , L } W_{l},l \in \left \{ 1,2,...,L \right \} Wl,l∈{1,2,...,L}表示从 l − 1 l-1 l−1层到 l l l层的权重矩阵,偏置为 b l b_{l} bl。第 l l l层的神经元个数为 M l M_{l} Ml。那么第 l l l层的连续值神经元 i i i通过ReLU层的计算如下:

考虑 a 0 = x a^{0}=x a0=x,x表示归一化后的输入,其中 x i ∈ [ 0 , 1 ] x_{i}\in [ 0,1] xi∈[0,1]。第 l 层 第 i 个 l层第i个 l层第i个SNN神经元在t时刻的膜电位用 V i l ( t ) V_{i}^{l}(t) Vil(t)表示,每个time step下的输入电位为:

在这里的 V t h r V_{thr} Vthr是阈值电位, Θ t , i l \Theta _{t,i}^{l} Θt,il指示着 t t t 时刻脉冲的产生与否:

时间窗口为T,每个time step size为 △ t ∈ R + \bigtriangleup t\in R^{+} △t∈R+,那么脉冲发射率最高为 r m a x = 1 / △ t r_{max}=1/\bigtriangleup t rmax=1/△t。第一层输入的发射率和常量的像素值或者说是RGB通道值有关,我们每个SNN神经元i的发射率为: r i l ( t ) : = N i l ( t ) / t r_{i}^{l}(t):=N_{i}^{l}(t)/t ril(t):=Nil(t)/t,这里的 N i l ( t ) : = ∑ t ′ = 1 t Θ t ′ , i l N_{i}^{l}(t):=\sum_{t^{'}=1}^{t}\Theta _{t^{'},i}^{l} Nil(t):=∑t′=1tΘt′,il,即为直到t时刻为止发射脉冲的个数。
ANN-to-SNN的原理正如Cao等人介绍的那样,提出了发射率 r i l r_{i}^{l} ril和原始ANN的激活值 a i l a_{i}^{l} ail正相关,在接下来,我们会对两者之间的关系作公式化的表述。
2.1.1. 膜方程
神经元 i i i在 t t t时刻的输入为 z i l ( t ) z_{i}^{l}(t) zil(t),此时的膜电位是要在原来的基础上加上 z i l ( t ) z_{i}^{l}(t) zil(t)得到 V i l ( t ) V_{i}^{l}(t) Vil(t),只有膜电位超过阈值 V t h r ∈ R + V_{thr}\in R^{+} Vthr∈R+时才会产生脉冲。一旦脉冲被产生,膜电位就被复位。现在我们讨论下两种复位的机制:reset to zero(将膜电位复位到一个基准值,通常是0)和 reset by subtraction(给现在的膜电位减去一个阈值 V t h r V_{thr} Vthr):

从这两个膜方程来看,我们可以得出略有不同的近似属性。在本节中,我们分析了第一个隐藏层并在2.1.2节将其扩展到更高层。我们假设输入电位 z i 1 > 0 z_{i}^{1}>0 zi1>0,这个假设在2.2.4节有证明。对于第一层神经元的输入(2)式可以通过 z i 1 = V t h r a i 1 z_{i}^{1}=V_{thr}a_{i}^{1} zi1=Vthrai1和ANN的激活值(1)式联系起来。为了将ANN的激活值和SNN的脉冲发射率关联起来,我们得到了下面的膜方程(4a)和(4b):

关于上面方程的推导本来是在补充材料里给出的,下面我们来看一下推导过程:
2.1.1.1 Reset to zero
我们的目标是得到脉冲发射率 r i 1 ( t ) r_{i}^{1}(t) ri1(t)和ANN激活值之间的关系。未来简化标记,我们去掉了层和神经元的索引,现在开始推导,仿真时间t内的平均发射率求和可以简化为:

我们之前已经做了一个假设——对于第一个隐藏层而言输入z是一个模拟常量(2.2.4节中有证明),并且使用 N ( t ) = ∑ t ′ = 1 t Θ t ′ N(t)=\sum_{t^{'}=1}^{t}\Theta _{t^{'}} N(t)=∑t′=1tΘt′,同时 ∑ t ′ = 1 t 1 = t / △ t \sum_{t^{'}=1}^{t}1=t/\bigtriangleup t ∑t′=1t1=t/△t,我们可以得到:

将 r m a x = 1 / △ t r_{max}=1/\bigtriangleup t rmax=1/△t带入上式,得:

又因为 ∑ t ′ = 1 t ( V ( t ′ ) − V ( t ′ − 1 ) ) = V ( t ) − V ( 0 ) \sum_{t^{'}=1}^{t}(V(t^{'})-V(t^{'}-1))=V(t)-V(0) ∑t′=1t(V(t′)−V(t′−1))=V(t)−V(0),带入上式得到:

Θ t \Theta _{t} Θt非1即0,S4的最后一项是对脉冲发放之前的膜电位求和,在reset-to-zero、constant input、constant threshold、no leak的情况下, t ′ t^{'} t′从1到t-1的阶段 Θ t ′ = 0 \Theta _{t^{'}}=0 Θt′=0,而每次膜电位都会增加一个相同的输入z,所以可以得到 ( n − 1 ) z < V t h r ⩽ n z (n-1)z<V_{thr}\leqslant nz (n−1)z<Vthr⩽nz,进而有:

将S5代入S4中,可以得到:

我们现在定义残差 ε \varepsilon ε为t时刻膜电位超过阈值的部分,即
![]()
将其代入S6式中,平均的脉冲发射率为:

最后,我们确保第一个隐藏层的输入为常量,即 z 1 = V t h r a 1 z^{1}=V_{thr}a^{1} z1=Vthra1,让 V ( 0 ) = 0 V(0)=0 V(0)=0,S8式可以转换为(5a):

2.1.1.2 Reset by subtraction
先对(4b) t ′ 从 1 到 t t^{'}从1到t t′从1到t求和,再取平均值,有:
1 t ∑ t ′ = 1 t V ( t ′ ) = 1 t ∑ t ′ = 1 t V ( t ′ − 1 ) + 1 t ∑ t ′ = 1 t z i l ( t ′ ) − 1 t ∑ t ′ = 1 t V t h r Θ t , i l \frac{1}{t}\sum_{t^{'}=1}^{t}V(t^{'})=\frac{1}{t}\sum_{t^{'}=1}^{t}V(t^{'}-1)+\frac{1}{t}\sum_{t^{'}=1}^{t}z_{i}^{l}(t^{'})-\frac{1}{t}\sum_{t^{'}=1}^{t}V_{thr}\Theta _{t,i}^{l} t1∑t′=1tV(t′)=t1∑t′=1tV(t′−1)+t1∑t′=1tzil(t′)−t1∑t′=1tVthrΘt,il
而 1 t ∑ t ′ = 1 t z i l ( t ′ ) = n z t \frac{1}{t}\sum_{t^{'}=1}^{t}z_{i}^{l}(t^{'})=\frac{nz}{t} t1∑t′=1tzil(t′)=tnz,且 t = n △ t , r m a x = 1 / △ t t=n\bigtriangleup t,r_{max}=1/\bigtriangleup t t=n△t,rmax=1/△t,所以有 1 t ∑ t ′ = 1 t z i l ( t ′ ) = z r m a x \frac{1}{t}\sum_{t^{'}=1}^{t}z_{i}^{l}(t^{'})=zr_{max} t1∑t′=1tzil(t′)=zrmax,省略下标,进而得到:
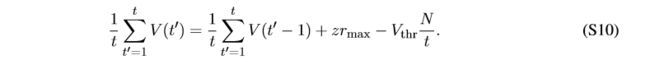
将 z 1 = V t h r a 1 和 r = N / t z^{1}=V_{thr}a^{1}和r=N/t z1=Vthra1和r=N/t代入S10中,得到:

令 V ( 0 ) = 0 V(0)=0 V(0)=0,S11变成了(5b)式。
————————————————————————————————————分界线
到这里对(5a)和(5b)的推到就结束了,我们来看看结果。正如我们在2.1节最后所期望的那样,脉冲发射率和ANN的激活值 a i 1 a_{i}^{1} ai1成比例,但是这个比例被一个额外的误差项减小了。在reset to zero的情况下,增加了一个乘法误差项,同时输入一直都是常量,对于同一个神经元 i 来说time steps n i 1 n_{i}^{1} ni1也是常量,膜电位超过阈值的那部分 ε i 1 = V i 1 ( n i 1 ) − V t h r = n i 1 ⋅ z i 1 − V t h r ⩾ 0 \varepsilon _{i}^{1}=V_{i}^{1}(n_{i}^{1})-V_{thr}=n_{i}^{1}\cdot z_{i}^{1}-V_{thr}\geqslant 0 εi1=Vi1(ni1)−Vthr=ni1⋅zi1−Vthr⩾0,在reset to zero时这个误差项最后被丢弃了,这将会导致发射率的减小从而造成信息损失。对于浅层网络和如MNIST这样的小数据集而言,这个误差项只是一个小问题,但是我们发现在深层中近似误差会累加从而降低分类错误率。我们也可以从等式(5a)观察到一个更大的 V t h r V_{thr} Vthr或者更小的输入可以改进近似结果。又 ( n i 1 − 1 ) z i 1 < V t h r ⩽ n i 1 z i 1 (n_{i}^{1}-1)z_{i}^{1}<V_{thr}\leqslant n_{i}^{1}z_{i}^{1} (ni1−1)zi1<Vthr⩽ni1zi1,我们发现近似误差被上面的输入 z i 1 z_{i}^{1} zi1而限制,这个视角解释了为什么Diehl等人的权重归一化可以提高表现:通过保证ANN的激活值足够小而不足以在single time step就可以使得膜电位大于阈值,我们保持 z i 1 = V t h r a i 1 z_{i}^{1}=V_{thr}a_{i}^{1} zi1=Vthrai1,因此 ε i 1 \varepsilon _{i}^{1} εi1很小,另一种改进近似的明显的方法就是减小 n i 1 n_{i}^{1} ni1来降低误差项,但是这会增加single time step内的计算成本。
reset by subtraction 机制改进了近似,这种方案更加适合深层网络,多余的电位 ε \varepsilon ε在reset时没有被丢弃,并用于下一次脉冲发射。因此,由于 ε \varepsilon ε引起的发射率误差在等式(5b)中消失了,相反,第一个隐藏层的发射率最终会收敛在 a i 1 r m a x a_{i}^{1}r_{max} ai1rmax,唯一的由于离散采样误差引起的近似误差也会随着时间消失。我们在3.1节通过实验仿真验证了这个机制的确导致了比Cao等人提出的转换更好的近似精度,尤其是在深层网络中 。
2.1.2. 更高层的发射率
之前的结果都建立在一个基础上——神经元在仿真时间内接受到的输入z是一个常量。当隐藏层的神经元发射脉冲时,这个条件仅对第一个隐藏层成立,并且我们用模拟电位的形式取代脉冲序列。在reset-by-subtraction这种条件下,我们分析得出近似误差是怎么在深层中传播的。为此,我们将SNN的输入 z i l z_{i}^{l} zil的表达式等式(2)插入到(4b)所示的膜等式(4b)中(针对 l > 1 l>1 l>1层),又 r m a x ∑ j = 1 M l − 1 W i j l Θ t , j l − 1 = 1 △ t ∑ j = 1 M l − 1 W i j l ∑ t ′ = 1 t Θ t ′ , j l − 1 = ∑ j = 1 M l − 1 W i j l N ( t ) t = ∑ j = 1 M l − 1 W i j l γ j l − 1 r_{max}\sum_{j=1}^{M^{l-1}}W_{ij}^{l}\Theta _{t,j}^{l-1}=\frac{1}{\bigtriangleup t}\sum_{j=1}^{M^{l-1}}W_{ij}^{l}\sum_{t^{'}=1}^{t}\Theta _{t^{'},j}^{l-1}=\sum_{j=1}^{M^{l-1}}W_{ij}^{l}\frac{N(t)}{t}=\sum_{j=1}^{M^{l-1}}W_{ij}^{l}\gamma _{j}^{l-1} rmax∑j=1Ml−1WijlΘt,jl−1=△t1∑j=1Ml−1Wijl∑t′=1tΘt′,jl−1=∑j=1Ml−1WijltN(t)=∑j=1Ml−1Wijlγjl−1,故得到:
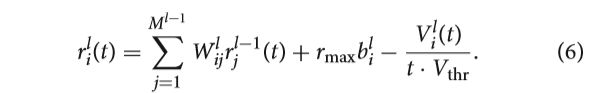
等式描述了第l层神经元的发射率被之前层的发射率的权重和所决定,正如等式(5b)中减去了一个随时间衰减的误差项一样,这个关系反应了每一层都要对权重和之前层的近似误差项乘积求和,然后再加上自己的近似误差项。将之前层的发射率迭代代入(6)式,其中 第一层的发射率用(5b)计算:

其中 △ V i l : = V i l ( t ) / ( t ⋅ V t h r ) \bigtriangleup V_{i}^{l}:=V_{i}^{l}(t)/(t\cdot V_{thr}) △Vil:=Vil(t)/(t⋅Vthr)。因此,第l层的神经元i接受一个输入脉冲序列,可以观察到越往后的层由于之前层神经元量化误差 △ V \bigtriangleup V △V的存在逐渐减小。这些误差逐层累加,这也解释了为什么实现与人工神经网络激活值高相关性的发射率需要更长的时间,和为什么SNN发射率在高层会恶化的原因。
2.2. ANN操作的脉冲实现
在本节中,我们介绍一些新方法改善深度SNN的分类错误率,这些方法将会允许一个更宽范围ANN的转换,也会减少SNN的近似误差。
2.2.1. Converting Biases
偏置在ANN中是一种标准结构,但是它在以前的ANN到SNN的转换方法中是明确排除在外的。在脉冲神经网络中,偏置可以简单地用一个和偏置符号相同的常量输入电位来实现。另外,Neftci等人之前也提到过可用额外常量脉冲(其发射率和ANN偏置大小成比例),尽管有时当偏置为负时需要反转脉冲的符号,2.1节介绍的理论也可以用到带偏置的神经元上,并且之后在2.2.2节中要介绍的参数归一化也将应用到偏置上。
2.2.2. Parameter Normalization
近似误差的来源之一就是在模拟SNN时的时间步长,神经元的发射率被限制在一个区间 [ 0 , r m a x ] [0,r_{max}] [0,rmax],然而ANN通常不会有这样的约束。权重归一化是被Diehl等人引入作为一种避免由于太高或太低的发射率而造成的近似误差的方法。通过使用一种“data-based weight normalization mechanism”的方法展示了将ANN转换为SNN时性能上的提升,我们将这个方法扩展到带有偏置的神经元上,提出了一种方法使得归一化过程对异常值更加稳健。
2.2.2.1. Normalization with biases
data-based权重归一化机制是基于用于ANN中的ReLU单元的线性度,它可以简单地扩展到偏置,通过线性的缩放所有的偏置和权重以使得ANN的激活值 a a a(正如等式(1)计算出来的值)对于所有的训练样本都小于1。为了保留一个层内编码的信息,一个层的参数需要联合缩放。定义 λ l = m a x [ a l ] \lambda ^{l}=max[a^{l}] λl=max[al],对权重 W l 和 偏 置 b l W^{l}和偏置b^{l} Wl和偏置bl的归一化可以通过 W l → W l λ l − 1 λ l 和 b l → b l / λ l W_{l}\rightarrow W_{l}\frac{\lambda _{l-1}}{\lambda _{l}}和b_{l}\rightarrow b_{l}/\lambda _{l} Wl→Wlλlλl−1和bl→bl/λl来完成。
2.2.2. Robust normalization
尽管权重归一化避免了SNN中的发射率饱和问题,但是它可能会导致非常低的发射率,因此需要增加信息到达更高层的延迟(即增大 n i l n_{i}^{l} nil)。我们参考了之前提到的“max-norm”算法,因为归一化因子 λ l \lambda ^{l} λl被设置为一个层内ANN激活值的最大值,通常激活值也是参考了训练数据中的一个大的子集。这是一个非常保守的方法,它确保了SNN的发射率很大可能不会超过最大的发射率 r m a x r_{max} rmax,缺点是这个过程很容易被单个异常样本所影响,从而导致较高的激活值,但对于大多数样本来说,发射率是在最大发射率之下的。
正如Figure 1A所示,这些的异常并不少见,Figure 1A中描述了对于16666个CIFAR 10的采样样本第一个卷积层中非零激活值的log-scale的分布,可以观察到最大的激活值要比处在所有激活值中99.9%处对应的激活值大三倍。Figure 1B展示了对于16666个采样样本同一层中所有ANN单元最大激活值的分布情况,反应了数据集之间比较大的方差,尖峰是远离绝对最大值的,这个分布解释了为什么通过最大值归一化会导致SNN有一个比较差的分类表现。对于大多数输入样本,一个层内最大激活值是远远低于被选择的归一化因子的,这将会导致驱动高层时发射率太低的问题,进而会导致比较差的分类结果。

我们提出了一个更加稳健的替代方案——将 λ l \lambda ^{l} λl设置为第l层所有激活值分布中比例为p处对应的激活值(p在[0, 100]之间),这个选择丢弃了额外的异常值,增加了一部分样本的SNN发射率,可能的缺点就是很小比例的神经元会饱和,所以选择归一化因子就是在饱和和不充分的发射率之间权衡。在接下来,我们将p定义为归一化尺度,并且"max-norm"对应p=100,表现比较好的典型p值的范围为[99.0, 99.999]。通常来讲,一小部分神经元饱和导致的分类错误率比要比发射率过低这种情况小很多,这种方法也可以在训练期间和BN层相结合,对每一层进行归一化,因此会使得异常值少很多。
2.2.3. BN层的转换
BN层减少了ANN中内部协变量的偏移,因此可以加速训练进程。BN层引入了额外的仿射变换,使得数据变成0均值、1方差。输入x经过BN层要做的变换为 γ σ ( x − μ ) + β \frac{\gamma}{\sigma}(x-\mu)+\beta σγ(x−μ)+β,这里的 γ , β , μ , σ \gamma,\beta,\mu,\sigma γ,β,μ,σ都是训练获得的参数。在训练之后,这些变换可以被集成到权重向量中,因此保留了BN的影响,但是消除了BN层进行归一化的计算需求。特别地,我们设置 W ~ i j l = γ i l σ i l W i j l , b ~ i l = γ i l σ i l ( b i l − μ i l ) + β i l \tilde{W}_{ij}^{l}=\frac{\gamma _{i}^{l}}{\sigma _{i}^{l}}W_{ij}^{l},\tilde{b}_{i}^{l}=\frac{\gamma _{i}^{l}}{\sigma _{i}^{l}}(b_{i}^{l}-\mu _{i}^{l})+\beta _{i}^{l} W~ijl=σilγilWijl,b~il=σilγil(bil−μil)+βil。这使得将BN层转换为SNN很简单,因为在将BN层折算进前层后,不需要对BN层进行额外的转换了,我们发现这个转换过程是零损失的,优势在于当BN层用于训练时得到的网络性能更好。
2.2.4. Analog Input to First Hidden Layer
因为基于事件的基准测试集很少见,传统的frame-based的图像数据集(比如MNIST或CIFAR)已经用于对转换后的SNN的分类错误率做评估。之前的方法经常将模拟的输入激活值、灰度值或RGB值转换为泊松发射率,但是这种转换对网络的发射引入了可变性,一定程度上损害了性能。
在这里,我们将模拟的输入激活值看作常量电位,遵从等式(2),对于第一个隐藏层的神经元来说,输入就是可以通过相关核和图片的模拟输入x相乘得到:

对于每一个神经元i, z i l z_{i}^{l} zil是常量,以后的每个time step膜电位都会加一个 z i l z_{i}^{l} zil。我们发现这个在低激活值方案中非常有效,但对于脉冲神经元的下采样提出了挑战。
2.2.5. Spiking Softmax
softmax通常用在深度ANN的输出,它会有一个归一化的效果,并且使得输出像是类别概率。之前的ANN-to-SNN转换的方法不会转换softmax层,而是通过在仿真期间神经元的脉冲发射率来确定预测的输出类别的,但是这个方法当最后一层接受的都是负输入时会失败,因为没有脉冲发射。
我们有三种方法来转换softmax层:
- 第一种是基于Nessler等人提出的机制,输出脉冲是由固定发射率的额外的泊松生成器触发的,脉冲神经元自己不发射,只是简单的累加它们的输入,脉冲是否发射由额外的生成器产生,softmax competition根据累加的膜电位触发;
- 第二种脉冲softmax函数是类似的,但是不依赖额外的时钟,为了确定神经元是否发射脉冲,我们需要计算脉冲电位的softmax输出,使得输出值在[0,1]之间,这两种方法的最终分类结果都是根据仿真时间内发射率最高神经元索引决定的。我们倾向于选择第二种方法,因为这种方法仅依赖于一个超参数;
- 第三种方法是基于我们只需要根据softmax层的输入膜电位就可以确定最终的分类结果,这个简化可以加速推断时间,也可以通过减少随机性来提高精度。这种方法在不需要坚持纯粹的脉冲网络时是很有吸引力的。
2.2.6. Spiking Max-Pooling Layers
在这里,我们提出了一个简单的转换max-pooling机制,输出单元包含一个门控功能,它只会让最大值发射率神经元通过,而丢弃其他神经元,门控功能通过计算前突触发射率的估计值来控制。
2.3. Counting Operations
先来定义几个标记符号:
f i n f_{in} fin:一个神经元输入的连接关系,比如在卷积层, f i n f_{in} fin就是2维卷积核的尺寸乘以前层的通道数得到的,在卷积层就是前层的神经元个数;
f o u t f_{out} fout:神经元和下层的连接关系,比如在卷积层 l l l,后面紧跟着第 l + 1 l+1 l+1个卷积层, f o u t f_{out} fout通常由第 l + 1 l+1 l+1个卷积层的步长决定,假如stride为1, f o u t f_{out} fout简单地由第 l + 1 l+1 l+1个卷积层的二维卷积核的尺寸乘以其通道数得到的。
其中 n l n_{l} nl为第 l l l层神经元的个数,因子2是由于每个 f i n f_in fin操作都是乘加运算,+1是由于需要加上偏置,这里没有考虑池化操作。
在SNN中,当神经元状态更新时只需要加法,那么在仿真时间T内SNN的总操作量为:

s l ( t ) s_{l}(t) sl(t)代表在t时刻第l层神经元发射的脉冲数量。
在ANN中,要对一张图片做分类,前向传播的成本是一个常量。在SNN中,图片在仿真周期内被呈现给网络,网络在每个time step都有一个预测输出,为了在每个time step衡量分类错误率和操作量,我们展示了SNN的错误率是如何随着操作量的增加而减小的。

两种不同的操作模式——single forward pass in ANN vs. continuous simulation in the SNN,一个众所周知的事实就是SNN只需要做加法的成本要比ANN中乘加运算的成本低很多,举个例子,Global Foundry 28nm进程展示了执行32-bit的浮点加法的成本要比MAC操作的成本低14x,相关的芯片区域面积也小了21x。同时也展示了内存访问要比计算的能耗高两个数量级。在ANN中,读卷积核的权重、内存中的神经元状态、将状态写回内存中在单个样本的前向传播过程中都只进行一次,相反,SNN中的内存访问是不可预测的,可能对于单个神经元要访问多次(这和对应的发射率有关),如果SNN需要的操作量比ANN低,那么等价地SNN在内存访问上也会有减少。直接在脉冲硬件平台如SpiNNaker或TrueNorth上的实现留待将来的工作,而且将其与在传统的ANN硬件加速器如Eyeriss上实现ANN的能耗成本做对比也是很有必要的。
3. Results
我们有两种方法来改善转换为SNN后的分类错误率:
- 在转换之前训练一个更好的ANN;
- 通过消除SNN的近似误差改善转换;
接下来在3.1和3.2节我们使用CIFAR-10数据集评估影响,在3.3节将SNN转换方法扩展到ImageNet数据集,在3.4节我们展示了SNN的精度和操作量之间的权衡,在给定的计算力预算下允许微调网络的性能。
3.1. Contribution of Improved ANN Architectures
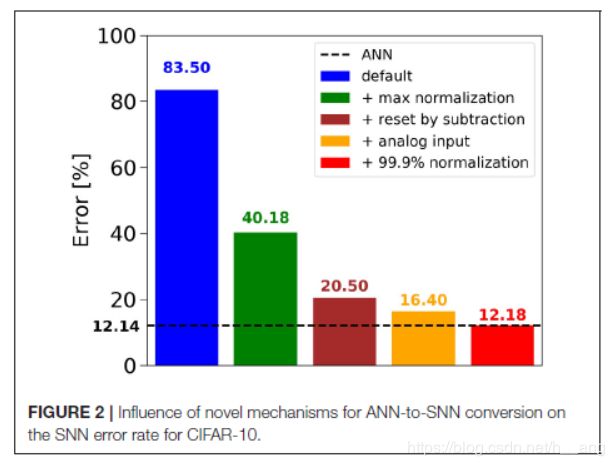
在第二节提出的方法允许被转换的CNN有偏置、softmax、batch-normalization、max-pooling层,这些提高了ANN的分类精度。我们的CIFAR-10上的网络结构为:4个卷积层(32 3x3 - 32 3x3 - 64 3x3 - 64 3x3),ReLU激活值,batch-normalization,2x2 max-pooling(在第2个和第4个卷积层之后),之后紧跟两个全连接层(512个神经元和10个神经元)和一个softmax输出。Table 1显示了ANN实现了12.14%的错误率,将偏置约束到0使得错误率增加为12.27%,用average-pooling进一步取代max-pooling时错误率为12.31%,消除softmax只使用ReLU会导致错误率变为30.56%。使用我们的新方法可以获得比之前ANN更好的性能。

3.2. Contribution of Improved SNN Conversion Methods
- —:ANN的错误率;
- default:no normalization、Poisson spike train input、reset-to-zero;
- 可以看出来,red bar的转换结果接近无损;
- accuracy-latency trade-off;

- ANN以每帧2.35MOps的计算量实现了1.04%的错误率;
- spiking model将计算量减小了2x,同时错误率只上升了1%(2.07%的错误率,1.07MOps/frame);
- 在1.47MOps时,SNN错误率为1.13%;

3.3. ImageNet
VGG和GoogLeNet被用来处理ImageNet数据集。
3.3.1. 瞬态动力学和电压钳位
section 2中提到的转换流水线对于MNIST和CIFAR-10数据集来说可以实现和ANN相当的错误率,但对于转换后的Iception-V3来说最初和ANN的错误率相差很大,主要原因有两点:
- 由于一些神经元的偏置或输入权重过大,神经元在仿真开始阶段经历了瞬态,在开始的几个time steps,发射脉冲之前都会累加输入脉冲,在第一层的神经元的发射率需要几个time steps就可以收敛到一个稳定的发射率,并且这个收敛时间在接受了瞬时变化输入的高层会增加,收敛时间在集成了高频输入的神经元会减少,但是在集成了低频脉冲的神经元会增加;
- 另外一个原因就是1x1的卷积层会造成一个大的瞬时响应,在这些层中,对于单个神经元的突触输入是前层的单列元素(长度为通道数),因此神经元的偏置或者强烈偏离的突触输入会决定输出范围。而随着核尺寸的增大,更多的脉冲会被聚集,会超多大偏置的影响;
为了克服神经元动态的瞬态负面影响,我们尝试了许多可能的解决方法,包括神经元状态的初始化、不同的reset机制和偏置放松方案。我们发现最成功的方法还是在最开始的N个time steps将膜电位钳位到0,N随着层深 l l l线性增加: N ( l ) = d ⋅ l N(l)=d \cdot l N(l)=d⋅l,斜率d代表时间延迟,d越长,就意味着下一层集成前层的输出之前,前层收敛到稳态的时间越长。
修正SNN状态变量的最简单的方法就是移除掉瞬态响应(如Figure S1所示,在补充材料中),膜电位钳位了10个time steps。

3.4. Combination with low-Precision Models
脉冲网络中神经元发射脉冲的频率与对应的ANN单元的激活值成正比,低精度目标激活值可以更快更准确地使用少量的脉冲事件来近似,举个例子,当激活值被量化为{0, 0.1, 0.2, 0.3,…,0.9, 1.0},脉冲神经元可以完美的在10个time steps内表达每一个值,另一方面,为了近似16位精度的浮点数,最坏情况下神经元需要在65536个time steps下保持激活。
为了展示在将给定模型转换为脉冲网络中低精度激活值的好处,我们应用2.2节中BinaryNet的方法,权重和激活值都约束到{0,+1}或者{-1,+1}。分别采用的是Heaviside(阶跃函数)和sign函数。为了解释BinaryNet中的负激活值,我们添加了第二个阈值-1,如果神经元阈值小于-1就发射一个幅度为-1的脉冲。
凭借着量化激活值,这两种SNN都可以在很少的操作内就近似达到ANN的错误率(如下图Figure 4所示)。BinaryNet SNN已经展示了和ANN目标错误率接近的错误率,像规范,在全精度模型中,ANN和SNN的错误率在操作量很小时相差较大,是随着计算量增加逐渐减小的。

