c语言实现1024bit大数欧几里德求逆元(6)

因为需要苟代码，需要知道欧几里德的定义，然后看了前人的解释，自己才可以继续编代码。
1.辗转相除法， 又名欧几里德算法(Euclidean algorithm)，是求两个正整数之最大公约数的算法。
其具体的算法是：设 a = qb + r，其中a，b，q，r都是整数，则 gcd(a,b) = gcd(b,r)，即 gcd(a,b) = gcd(b,a%b)。
证明：
令a=mc,b=nc,gcd(a,b)=c,且（m,n）=1
r=a-qb=mc-qnc=(m-qn)c
其中(m-qn)与n互素，（若(m-qn)与n不互素，设m-qn=xd,n=yd,可以推出m=qn+xd=qyd+xd=(qy+x)d,gcd(m,n)=d,与已知矛盾）
故 gcd(b,r)=c
gcd(a,b) = gcd(b,r)
1769 和 551的最大公因子是29

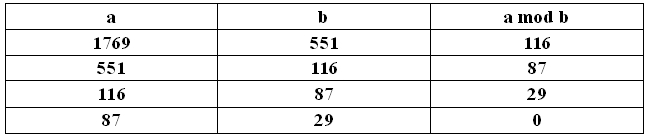
迭代实现欧几里德算法：

int gcd(int a,int b)
{
return a%b?gcd(b,a%b):b;
}

非迭代实现欧几里德算法：

int gcd(int a, int b)
{
    while(b)
    {
        int t = b;
        b = a % b;
        a = t;
    }
    return a;
}

辗转相除法的运算速度为 O(n)，其中 n 为输入数值的位数。
2.辗转相除法求逆元
贝祖等式(又称"裴蜀定理"[2])：对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性丢番图方程（称为裴蜀等式）：
ax + by = m 有整数解时当且仅当m是d的倍数。
裴蜀等式有解时必然有无穷多个整数解，每组解x、y都称为裴蜀数。
特别来说，方程 ax+by=1 有整数解当且仅当整数a和b互素。
对于一个例子47和23 gcd（113,47）=1
113=47 *2+ 19
47=19 *2+9
19=9 *2+1
倒推：
19-9 *2=1
（113-47 *2）-（47-19 *2） *2=1
（113-47 *2）-（47-（113-47 *2） *2） *2=1
5 *113-47 *12=1

设：a>b。
if b=0:
gcd(a,b)=a,可以得到x=1,y=0
if(ab)!=0:
gcd(a,b)=gcd(b,a mod b)
ax1+by1=bx2+(a-(a/b)*b)y2=ay2+bx2-(a/b)*by2;
x1=y2
y1=x2-(a/b)*y2
可以迭代，直到b=0
迭代方法求欧几里德逆元

int ex_gcd(int a,int b,int &x,int &y)       
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    int r=ex_gcd(b,a%b,x,y);
    int t=x;
    x=y;
    y=t-a/b*y;
    return r;
}

非迭代求欧几里德逆元[2]
给定两个正整数m和n， 计算他们的最大公因数d，并计算两个未必为正数的整数 a 和 b, 使得 am+bn=d.
a′←b←1,a←b′←0,c←m,d←n.a′←b←1,a←b′←0,c←m,d←n.
while(r!=0){.
q=c/d;r=c%d;
置 c←d,d←r,t←a′,a′←a,a←t−qa,t←b′,b′←b,b←t−qb ;
}

int exgcd(int m, int n, int &x, int &y) {
    if (n == 0) {
        x = 1; y = 0;
        return m;
    }
    int a, a1, b, b1, c, d, q, r, t;
    a1 = b = 1;
    a = b1 = 0;
    c = m; d = n;

    q = c/d; r = c%d;
    while (r) {
        c = d;
        d = r;
        t = a1;
        a1 = a;
        a = t - q * a;
        t = b1;
        b1 = b;
        b = t - q * b;

        q = c/d;
        r = c%d;
    }
    x = a; y = b;
    return d;
}

上文都是笔记，接下来仿照非迭代求欧几里德逆元的大数求法

/****************************************************************************************************
求不定方程ax-by的最小整数解
调用方式Inv(m,n,z)
返回值：z，满足：mz mod n=1
*****************************************************************************************************/


void Inv(unsigned int x[], unsigned int y[], unsigned int *z)
{
	unsigned int a[MAX], b[MAX], c[MAX], d[MAX], e[MAX], f[MAX];
	int s, t;
	Init(a);
	Init(b);
	Init(c);
	Init(d);
	Init(e);
	Init(f);
	if (Cmp(x, y) >= 0)
		Mod_Big(x, y, x);
	Mov_Big(y, a);
	Mov_Big(x, b);
	Mov_Long(0, c);
	Mov_Long(1, d);
	s = t = 1;
	while ((b[0] != 1) || (b[1] != 0))
	{
		Div_Big(a, b, e);
		Mod_Big(a, b, f);
		Mov_Big(b, a);
		Mov_Big(f, b);
		Mov_Big(d, f);
		Mul_Big(d, e, d);
		if (s == t)
		{
			if (Cmp(c, d) >= 0)
				Sub_Big(c, d, d);
			else
			{
				Sub_Big(d, c, d);
				t = 0;
			}
		}
		else
		{
			Add_Big(c, d, d);
			s = 1 - s;
			t = 1 - t;
		}
		Mov_Big(f, c);
	}
	if (s == 0)
		Sub_Big(y, c, c);
	if (Cmp(c, y) >= 0)
		Mod_Big(c, y, c);
	Mov_Big(c, z);


}

参考文献：
[1]:https://baike.so.com/doc/5939601-6152534.html欧几里德百科
[2]:https://blog.csdn.net/yoer77/article/details/69568676