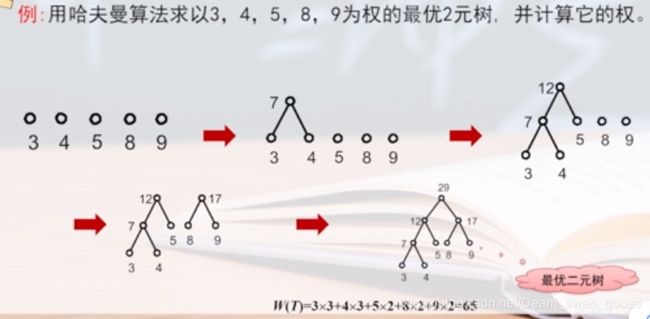
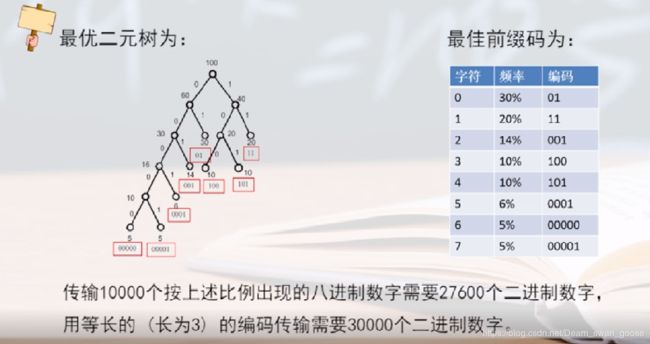
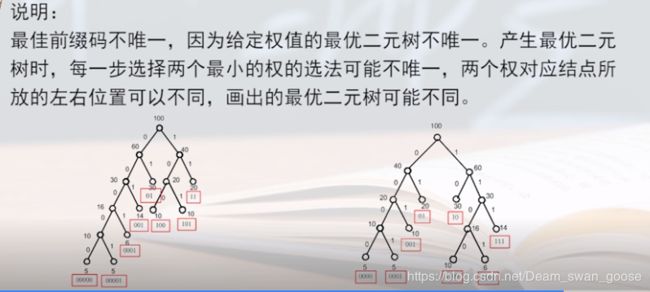
第五章 树和二叉树 —— 哈夫曼算法

哈夫曼算法

看到例题就懂了

最佳前缀码：

例题：


注意最佳前缀码可能是不唯一的。

---------------------------------------↓↓↓↓↓↓↓↓↓↓↓↓↓----------------------------------------
以下部分转载自：https://blog.csdn.net/harington/article/details/84202659
本人对该博主的代码加以修改和注释。

赫夫曼树的编码 代码 解码 建树过程

现在让我们一步一步构思

从最简单的开始，先给你 A B C D 4个节点 权值分别为 5 4 2 7

把他们一起存到一个数组内，然后 遍历 找到2个权值最小的 节点相加然后加入数组，标记一下，这两个及节点就被删除了，两个节点相加得到新的节点，加入到数组中，之后再继续 遍历 找到权值最小的两个点，继续重复上述操作，直到所有前面的 最初的 4 个节点都用过。（下面数组我们对第0列弃用，方便填下标）

下标	0	1	2	3	4	5	6	7
weight	0	5	4	2	7	0	0	0
parent	0	0	0	0	0	0	0	0
lchild	0	0	0	0	0	0	0	0
rchild	0	0	0	0	0	0	0	0

我们进行第一次遍历 找到最小的两个数 4 2 然后让他们作为左右子树构造成一个 二叉树 将这个 新的权值 2+4 = 6填入到下标第一空的地方，将 2 和 4 的parent 改为 新建权值的下标 将 新建节点的左右子树 改为两个节点的 下标

下标	0	1	2	3	4	5	6	7
weight	0	5	4	2	7	6	0	0
parent	0	0	5	5	0	0	0	0
lchild	0	0	0	0	0	2	0	0
rchild	0	0	0	0	0	3	0	0

之后继续遍历 weight 从第1个 到 第5个 找到 权值最小的两个（2 和 4已经被用过了）找到 5 和 6，继续建树 。新建树的权值为 11 ，然后改 5 和 6 的parent 为 新建权值的下标 6.改新建权值的 lchild为 1 。rchild 为 5。

下标	0	1	2	3	4	5	6	7
weight	0	5	4	2	7	6	11	0
parent	0	6	5	5	0	6	0	0
lchild	0	0	0	0	0	2	1	0
rchild	0	0	0	0	0	3	5	0

然后我们继续遍历找到 7 和 11 继续建树，加到数组的最后一个位置 改 7 和 11 的parent 改为 7, 新建节点18 的lchild 为 权值为7的下标4 .新建节点18 的 rchild 为权值为11 的下标6.这时所有的节点都用完了，我们构建赫夫曼树完成。

下标	0	1	2	3	4	5	6	7
weight	0	5	4	2	7	6	11	18
parent	0	6	5	5	7	6	7	0
lchild	0	0	0	0	0	2	1	4
rchild	0	0	0	0	0	3	5	6

然后求每个字符的Huffman编码。

举个例子，先找第一个 字符的huffman编码，也就是权值为 5 的赫夫曼编码，

1）先构建一个栈。

2）然后找第一个字符的 parent，判断是lchild 还是 rchild。（parent 是 6）找到下标为6的列

3）判断是lchild 还是 rchild。如果是lchild 则向栈中 压入0，如果是rchild 则向栈中压入1.（左孩子，把0压入栈中）

4）然后继续找parent。（找到6（权值11）的parent，下标为 7），重复操作 （3）操作（4）直到 Parent 变为0结束（也就是根节点）。然后弹栈，用一个数组接收。

然后我们求出第一个字符的 赫夫曼编码是 10

实验题：
给定报文中26个字母a-z及空格的出现频率{64, 13, 22, 32, 103, 21, 15, 47, 57, 1, 5, 32, 20, 57, 63, 15, 1, 48, 51, 80, 23, 8, 18, 1, 16, 1, 168}，构建哈夫曼树并为这27个字符编制哈夫曼编码，并输出。模拟发送端，从键盘输入字符串，以%为结束标记，在屏幕上输出输入串的编码；模拟接收端，从键盘上输入0-1哈夫曼编码串，翻译出对应的原文。

• 模拟发送端
  输入：I love you
  输出：01101111011110011100000010111100011100100001
• 模拟接收端 输入
  输入：01101101111011000111111010111101101001100001
  输出：it is a dog

代码如下：

#include

using namespace std;


typedef struct
{
    int weight;
    int parent, lchild, rchild;
} HTNode, *HuffmanTree;
typedef char **HuffmanCode;


void Select(HuffmanTree &HT, int end, int &s1, int &s2)		//找出最小的两个值。两个最小的值得下标记录到 s1 s2中。
{
    int min1 = 0x3f3f3f, min2 = 0x3f3f3f;//先将最小值定义为无穷大方便之后替换
    for(int i = 1; i <= end; i++)
    {
        if(HT[i].parent == 0 && HT[i].weight < min1)//在没有父结点的结点中循环找到权值最小的
        {
            min1 =  HT[i].weight;
            s1 = i;
        }
    }
    for(int i = 1; i <= end; i++)
    {
        if(HT[i].parent == 0 && HT[i].weight < min2 && s1 != i)//找出第二小的
        {
            min2 = HT[i].weight;
            s2 = i;
        }
    }
}

void HuffmanCoding(HuffmanTree &HT, HuffmanCode &HC, int *w, int n) //创建哈夫曼树和哈夫曼编码
{

    int i, s1, s2;
    HuffmanTree p;
    if(n <= 1)
        return ;//返回空地址
    int m = 2 * n - 1;//无度数为1的结点，故一共有2n-1个结点

    HT = (HuffmanTree) malloc((m + 1) * sizeof(HTNode));//分配空间
    for(p = HT + 1, i = 1; i <= n; i++, p++, w++)//从下标为1的位置开始把权值导入，父亲和孩子在最开始都没有
    {
        *p = {*w, 0, 0, 0};
    }


    for(; i <= m; i++, p++)//把后面的全初始化为0
        *p = {0, 0, 0, 0};

    for(i = n + 1; i <= m; i++)//从下标为n+1处开始赋值
    {

        Select(HT, i-1, s1, s2);//选择范围是0——n
        HT[i].weight = HT[s1].weight + HT[s2].weight;//将最小的两个先合并
        HT[s1].parent = i;
        HT[s2].parent = i;//这两个的父亲结点自然就是下标为i处
        HT[i].lchild = s1;
        HT[i].rchild = s2;//下标为i的结点的孩子结点就是他俩
    }

    //从叶子到根逆向求每个字符的哈夫曼树编码
    stack<char> s;//声明存放char类型的stack容器s
    for(i = 1; i <= n; i++)
    {

        int temp = i, p, k = 0;
        p = HT[temp].parent;
        while(p)
        {
            if(HT[p].lchild == temp)//左孩子入栈0
                s.push('0');
            if(HT[p].rchild == temp)//有孩子入栈1
                s.push('1');
            temp = p;
            p = HT[temp].parent;//更新父结点
            k++;
        }

        int j = 0;
        while(!s.empty())
        {
            HC[i][++j] = s.top();//将栈中的01序列存放在数组中
            s.pop();
        }
        HC[i][0] = j;//记录每个结点01序列的个数，方便循环输出
    }
}

void showHuffmanCode(HuffmanCode HC) 		//显示每个字符的哈夫曼编码
{
    char c ;
    for(int i = 1; i <= 27; i++)
    {
        if(i != 27)
        {
            c = i + 'A' - 1;
            cout << c << "的哈夫曼编码是：";
        }
        else
        {
            cout << "空格的哈夫曼编码是：";
        }
        for(int j = 1; j <= HC[i][0]; j++)
        {
            cout << HC[i][j];//输出哈夫曼编码
        }
        cout << endl;
    }
}


void TanserString(HuffmanCode HC,string s)	//将字符转化为哈夫曼编码
{
    string ss;
    for(int i = 0; i < s.length(); i++)
    {
        if(s[i] >= 'A' && s[i] <= 'Z')
            s[i] += 32;//转化为小写
        if(s[i] == ' ')
            s[i] = 'z' + 1;
    }

    for(int i = 0; i < s.length(); i++)
    {
        for(int j = 1; j <= HC[s[i] - 'a' + 1][0] ; j++)
            ss += HC[s[i] - 'a' + 1][j];//按字符类型相加
    }
    cout << ss << endl;
}


void TanserHuffmanCode(HuffmanCode HC,string s)	//将哈夫曼码变为字符
{
    string ss = "", s1 = "";
    string t[27];
    for(int i = 0 ; i < 27 ; i++) //将27个字符的哈夫曼编码存在数组t中
    {
        t[i] = "";
        for(int k = 1; k <= HC[i + 1][0] ; k++)
        {
            t[i] += HC[i + 1][k];
        }
    }
    for(int i = 0; i < s.size(); i++)
    {
        ss += s[i];//一直读取后面的编码直到有字符与其对应
        for(int j = 0; j < 27; j++)
        {
            if(ss == t[j])
            {

                ss = "";//将前面的清空，继续寻找下一组匹配的编码
                if(j != 26)
                {
                    s1 += j + 'a' ;
                }

                else if(j == 26)
                {
                    s1 += ' ';
                }
            }
        }
    }
    cout << s1 << endl;
}

void help()
{
    cout << "************************************************************" << endl;
    cout << "********   1.输入HuffmanTree的参数                      ****" << endl;
    cout << "********   2.初始化HuffmanTree参数.《含有26字母及空格》 ****" << endl;
    cout << "********   3.创建HuffmanTree和编码表。                  ****" << endl;
    cout << "********   4.输出编码表。                               ****" << endl;
    cout << "********   5.输入编码，并翻译为字符。                   ****" << endl;
    cout << "********   6.输入字符，并实现转码                       ****" << endl;
    cout << "********   7.退出                                       ****" << endl;
    cout << "************************************************************" << endl;
}



int main ()
{
    HuffmanTree HT;
    HuffmanCode HC;
    string s;
    HC = (HuffmanCode) malloc ((27+1) * sizeof(char *));
    for(int i = 1; i <= 28 ; i++)
        HC[i] = (char *)malloc((27+1) * sizeof(char));//HC是二维的故分配两次
    help();
    int a[27] = {64, 13, 22, 32, 103, 21, 15, 47, 57, 1, 5, 32, 20, 57, 63, 15, 1, 48, 51, 80, 23, 8, 18, 1, 16, 1, 168};

    int operator_code;
    while (1)
    {
        cout << "请输入操作 ：" << endl;
        cin >> operator_code;
        if(operator_code == 1)
        {
            HuffmanCoding(HT, HC, a, 27);
            cout << "创建成功，1,2,3已完成，无需输入2,3" << endl;
        }
        else if(operator_code == 4)
        {
            showHuffmanCode(HC);
        }
        else if(operator_code == 5)
        {
            cout << "请输入HuffmanCode：";
            cin>>s;
            TanserHuffmanCode(HC,s);
        }
        else if(operator_code == 6)
        {
            getchar();//将输入字符存放在缓冲区域内，直到按回车为止
            cout << "请输入字符：";
            getline(cin,s);//将输入内容传递给s
            TanserString(HC,s);
        }
        else if( operator_code == 7)
        {
            break;
        }
        else
        {
            cout << "输入违法请重新输入" << endl;
        }
    }
    return 0;
}