n^n的个位数字及求和情况

引言

记得初中还是小学的时候经常会做一种找规律的题，9的n次方的个位数规律：

9,81,729,6561,59049,531441......

可以发现个位数的规律是9,1,9,1,9,1

由乘法的原理可知：两个数相乘，所得积的个位数=原两个数的个位数相乘所得积的个位数。

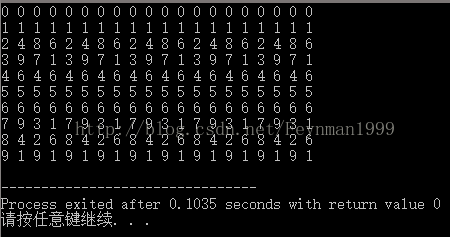
因为一个数的个位数在0~9的范围内，可知它们不停的乘以自身，个位数一定是有循环节的：

例如0永远是0,1永远是1,2的循环节是2,4,8,6......

打表后可以发现规律：

思路

所以当我们求n^n的个位数时(1<=n<=1*10^18),可用long long存n,%10得到个位数。(题外话：如果想到了大整数取模问题，可以参见http://blog.csdn.net/feynman1999/article/details/59117616)

之后利用已经发现的“个位数”规律即可求出n次方后的个位数

代码示例

#include
using namespace std;

int a[10][4]={{0},{1},{6,2,4,8},{1,3,9,7},{6,4},
{5},{6},{1,7,9,3},{6,8,4,2},{1,9}};//规律数组 

int main()
{
	long long n;
	while(cin>>n)
	{
		switch(n%10)
		{
			case 0:
			case 1:
			case 5:
			case 6:
				cout<

延伸   NBUT 1674

计算1^1+2^2+3^3.......+n^n的和的个位数

Input

输入整数 T （T个case）

输入整型 n （n < 10^18)

Output

输出算式的答案的个位数

Sample Input

3
1
2
3

Sample Output

1
5
2

思路

如果直接计算，n到e18，显然不可行，所以寻求规律

取个位数是2的数：2^2,12^12,22^22,32^32,42^42......

      其结果等同于：2^2,2^12,2^22,2^32,2^42

又由前面引言所得结论，2的循环节长为4：{2,4,8,6}  幂指数2,12,22,32,42，隔10出现一次，LCM（4,10）=20

所以每20个数中会有两个以2为个位数满足循环规律，如 2^2+2^12 =2^22+2^32=2^42+2^52......

这是个位数为2的情况，同理，因为n^n个位数情况循环节最大为4（还有1和2），2这样循环节为4的数满足20一循环，像1,5,6这样（循环节为1）自然也满足了。所以可知对于本题20是一个循环节。

代码示例

#include
#include
using namespace std;
int a[10][4]={{0},{1},{6,2,4,8},{1,3,9,7},{6,4},{5},{6},
              {1,7,9,3},{6,8,4,2},{1,9}};

int arr[22];

int main()
{
    int t,number,sum;
    long long m,n;
    //scanf("%d",&number);
    cin>>t;
    while(t--)
    {
        sum=0;
        cin>>n;
        m=n/20;//看有多少循环节
        m=4*m;//经计算，一个循环节的和的个位数是4,将这些个位数求和
        n=n%20;//重新定位n
        for(number=1;number<=n;number++){
        switch(number%10)
        {
            case 0:
            case 1:
            case 5:
            case 6:
            arr[number]=a[number%10][0];
            //printf("%d ",a[number%10][0]);
            break;
            case 2:
            case 3:
            case 7:
            case 8:
            arr[number]=a[number%10][number%4];
            //printf("%d ",a[number%10][number%4]);
            break;
            case 4:
            case 9:
            arr[number]=a[number%10][number%2];
            //printf("%d ",a[number%10][number%2]);
            break;
        }
        //if(number%10==0) printf("\n");
        }
        for(int i=1;i<=n;++i) sum+=arr[i];

        m+=sum;//加到m上
        cout<