感知机及Python实现

本文将讲解感知机的原理以及笔者使用Python语言对其的实现：

感知机原理

  什么叫感知机呢？
  在李航老师《统计学习方法》中是这么讲的：“感知机（perceptron）是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1和-1二值。”
  从定义我们可以看出，感知机其实就是能够实现一个二分类问题的表达式或函数。关于二分类问题，是指问题只可以被分为两类的问题，比如人类从性别上分可分为男性和女性，就是一个典型的二分类问题，还有只有黑球和白球的分类等等。那这样的问题如何让机器去实现呢？当然还得从数学上去考虑，如果我们把正确的分类标记为+1，错误的分类标为-1的话，只需要找到一个满足条件的函数去实现它就可以了。
  符号函数（一般用sign(x)表示）是很有用的一类函数，其表达式为：

$\{\begin{array}{l}sign(x)=1,x>0\\ sign(x)=0,x=0\\ sign(x)=-1,x<0\end{array}$​
  函数图像为：

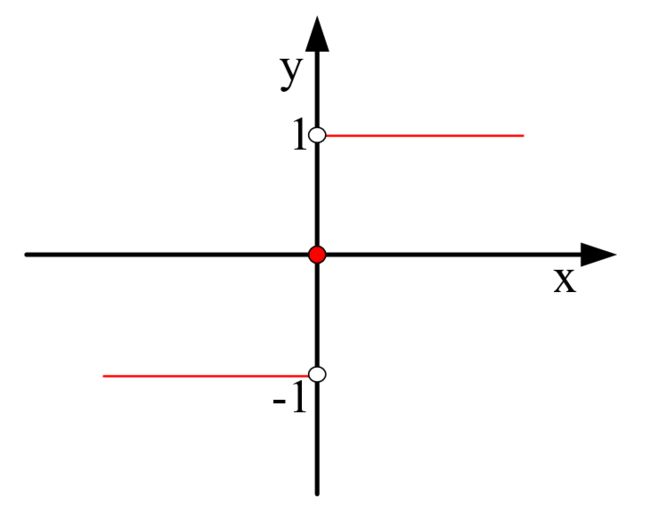
  即：当符号函数的自变量值大于0时其结果为1，自变量值小于0时其结果为-1，自变量等于0时值为0。那么，对于一个二分类问题，我们就可以利用符号函数的性质来解决我们的实际问题。下图坐标系中的方框和圆形就可以作为一个二分类的问题，当然，其分法有n多种，笔者画出了四种分法，哪一种最好呢？红线的分法应该是较为理想的，因为从目前方框和圆形的分布趋势我们有理由相信：即使有更多的方框或者圆形出现，按目前的趋势来讲红线依然有可能正确地分类，而其他颜色的线条则不然。

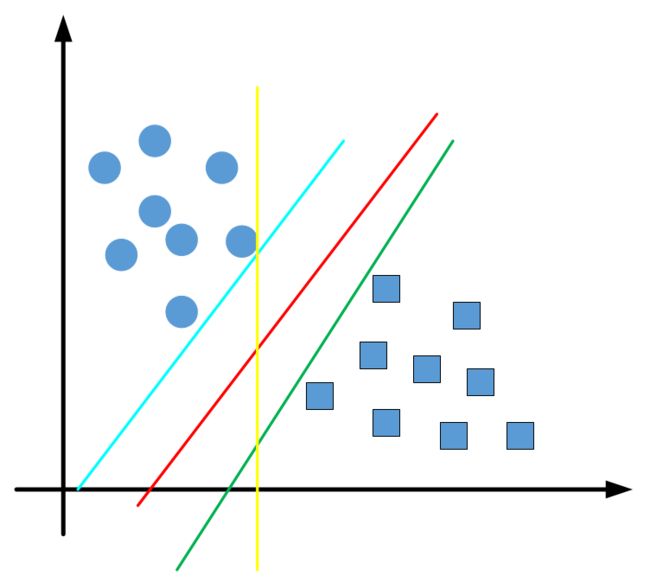
  那么，在坐标系中，我们将这些方框和圆圈可以表示为实际的坐标 $\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\}$，则我们的问题依然是去找一个这样的线（我们称满足这条线的方程为超平面），使得能够将这些属于二类的坐标点被正确地分类。这条线的表达式正是我们想要的，也就是我们所讲的 感知机。为了确定这样的感知机，我们需要确定一个学习策略，并定义一个损失函数使得该损失函数极小化。损失函数一般的选择方式是误分类点的总数，然而在选择感知机的过程中误分类点的总数不能直观地去改进我们的超平面，因此不能被很好地利用以改进我们的感知机。
  那么我们还得从感知机本身出发去考虑：
  从前面的讲解我们可以知道，感知机其实是一个线性方程，在二维平面坐标系中我们可以将其表示为 $Ax+By+C=0$   对于该方程，二维平面上任意一点 $P(x_0,y_0)$到任意一条直线 $Ax+By+C=0$的距离可以表示为： $d=\frac{A{x}_0+B{y}_0+C}{\sqrt{A^2+B^2}}$   那么我们可以选择将误分类的点到超平面的总距离作为损失函数。如果我们用 $w\cdot x+b=0$表示 $Ax+By+C=0$，那么我们分类问题中输入空间 $R^n$中任意一点 $x_0$到超平面的距离为数学中我们知道平面直角坐标系内任意一点到任意一条直线之间的距离可公式为： $\frac{1}{||w||}|w\cdot x_0+b|$ 其中 $||w||$是 $w$的 $L_2$范数。
  对于误分类点来说， $-y_i(w\cdot x_i+b)>0$，因为误分类时， $w\cdot x_i+b>0$，我们最初的定义误分类标记为 $-1$。【注意，这里的 $y_i$和 $Ax+By+C=0$中的 $y_i$不是一回事，这里 $y_i$表示点的分类标记。在我们用 $w\cdot x+b=0$表示 $Ax+By+C=0$时进行了一定的转换，即： $w=(w^{(1)},w^{(2)}{)}^T$， $x=(x^{(1)},x^{(2)}{)}^T$，那么， $w\cdot x+b=w^{(1)}{x}^{(1)}+w^{(2)}{x}^{(2)}+b$，也就是我们用 $w^{(1)},w^{(2)},x^{(1)},x^{(2)},b$分别表示了方程 $Ax+By+C=0$中的 $A,B,x,y,C$】
  如果假设超平面 $S$的误分类点集合为 $M$,那么所有误分类点到超平面 $S$的总距离为 $-\frac{1}{||w||}\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$ 方程给定后， $w$的值是一定的，那么我们可以不考虑 $-\frac{1}{||w||}$，直接将 $\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$作为感知机学习的损失函数。即给定训练集 $T=\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\}$，感知机的损失函数为： $L(w,b)=-\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$ 从表达式我们可以看出，损失函数的值非负的。如果没有误分类点，其值为 $0$，在误分类时，损失函数是参数 $w,b$的线性函数，则损失函数 $L(w,b)$是 $w,b$的连续可导函数。
  连续可导有什么用呢？回到最初的问题，我们的目标是求一个感知机，也就是能够将平面上的点正确二分类的方程 $w\cdot x+b=0$，在有误分类的情况发生时，不断修改 $w$和 $b$的值使得误分类的点越来越少，也就是让损失函数的值越来越小直至为 $0$。由于损失函数是关于 $w,b$连续可导的，其导数为： ${\nabla }_{w}L(w,b)=-\sum _{x_i\in M}{y}_i\cdot x_i$ ${\nabla }_{b}L(w,b)=-\sum _{x_i\in M}{y}_i$
  对于 $w$和 $b$的修改，我们可以随机选取一个误分类点 $(x_i,y_i)$，对 $w,b$进行更新： $w\leftarrow w+\eta y_i{x}_i$ $b\leftarrow b+\eta y_i$
  式中 $\eta (0<\eta \le 1)$是步长，又称为学习率（learning rate）。这样就可以通过不断跌代从而修改 $w$和 $b$的值使得损失函数不断减小直至为 $0$。
  可以看出，感知机学习的算法是误分类驱动的，在我们修改 $w,b$随机选取了一个点进行更新，我们将这个方法叫随机梯度下降法（stochastic gradient descent）。综上，感知机学习算法可以如下表示：
输入： 训练数据集 $T=\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\}$，其中， $x_i\in R^n,y_i\in \{-1,+1\},i=1,2,\cdots ,n;$ $\eta (0<\eta \le 1)$；
输出： $w,b$，感知机模型 $f(x)=sign(w\cdot x+b)$

1. 选取初值$w_0,b_0$
2. 在训练集中选取数据$(x_i,y_i)$
3. 如果$y_i(w\cdot x_i+b)\le 0$
   $\begin{array}{l}w\leftarrow w+\eta y_i{x}_i\\ b\leftarrow b+\eta y_i\end{array}$
4. 转至2.，直至训练集中没有误分类的点。

以上就是我们感知机的原理部分，接下来，我们将使用Python语言将其实现：

感知机的Python实现

话不多说，直接上python代码：

#   -*- encoding:utf-8 -*-
#   The entire code is used to implement the perceptron
"""
Created on Tuesday, 24 December 14:58 2019
@author:Jeaten
@email:[email protected]
"""
import numpy as np
import random
def data():
    '''
   该函数用于产生训练数据
    :return: 返回特征和标签
    '''
    train = [((3, 3), 1), ((4, 3), 1), ((1, 1), -1)]#((x,y),c):(x,y)为数据的坐标，c为所属类别
    feature=[]
    label=[]
    for i in train:
        feature.append(i[0])
        label.append(i[1])
    feature=np.array(feature)
    label=np.array(label)
    return feature,label
class perceptron:
    def __init__(self):
        '''
         :param w:感知机的权重
         :param b:感知机的偏置
         :param learning_rate:学习率
        '''
        self.w = np.array([0,0])
        self.b=0
        self.learning_rate=1
    def update(self,w,x,y,b):
        '''
        该函数用于参数的更新
        :param w: 权重
        :param x: 数据的特征
        :param y: 数据的标签
        :param b: 数据的偏置
        :return: 无
        '''
        self.w=w+self.learning_rate*x*y
        self.b=b+self.learning_rate*y
    def sign(self,w,x,b):
        '''
        该部分为符号函数
        :return 返回计算后的符号函数的值
        '''
        return np.sign(np.dot(w,x)+b)
    def train(self,feature,label):
        '''
        该函数用于训练感知机
        :param feature: 特征
        :param label: 标签（数据点所属类别）
        :return: 返回最终训练好模型（参数）
        '''
        stop=True
        while stop:
            count=len(feature)
            for i in range(len(feature)):
                if self.sign(self.w,feature[i],self.b)*label[i]<=0:
                    print( "分类错误！误分类点为:", feature[i] )
                    self.update( self.w, feature[i], label[i], self.b )
                else:
                    count -= 1
                if count == 0:
                    stop = False
        print( "最终权重 w:", self.w, "最终偏置 b:", self.b )
        return self.w,self.b
    def train_rand(self,feature,label):
        '''
        该函数使用随机选择数据点来进行训练（随机梯度下降法）
        :param feature: 特征
        :param label: 标签（数据点所属类别）
        :return: 返回最终训练好模型（参数）
        '''
        stop=True
        while stop:
            count=len(feature)
            index=[i for i in range(len(feature))]
            random.shuffle(index)
            for i in index:
                if self.sign(self.w,feature[i],self.b)*label[i]<=0:
                    print( "分类错误！误分类点为:",feature[i])
                    self.update(self.w,feature[i],label[i],self.b)
                else:
                    count-=1
            if count==0:
                stop=False
        print("最终w:",self.w,"最终b:",self.b)
        return self.w,self.b
class show:
    def draw_curve(self, data,w,b):
        '''
        该函数应用于查看拟合效果
        :param data: 数据点
        :param w: 权重
        :param b: 偏置
        :return: 无
        '''
        import matplotlib.pyplot as plt
        data,label=data
        coordinate_x=[]
        for i in data:
            coordinate_x.append(i[0])
        coordinate_y=[]
        for i in range(len(data)):
            coordinate_x.append(data[i][0])
            coordinate_y.append(data[i][1])
            if label[i]==1:
                plt.plot(data[i][0], data[i][1],'o'+'r',label='right',ms=10)
            else:
                plt.plot(data[i][0], data[i][1],'*'+'g',label='error',ms=10 )
        d_x=np.arange(0,max(coordinate_x),1)
        d_y=[]
        for i in d_x:
            d_y.append(-(w[0]*i+b)/w[1])#一定的学习率下可能会有除0错误
        plt.plot(d_x,d_y,)
        plt.show()
        return True
if __name__ == '__main__':
    feature,label=data()
    x=np.array(feature)
    y=np.array(label)
    neuron=perceptron()
    show=show()
    w, b = neuron.train( x, y )#按序调整
    # w,b=neuron.train_rand(x,y)#使用随机梯度下降法
    show.draw_curve( data(), w,b )

首先让我们跑一下看看效果，得到权重为w=[1 1],偏置为b=-3，其结果如下图所示：

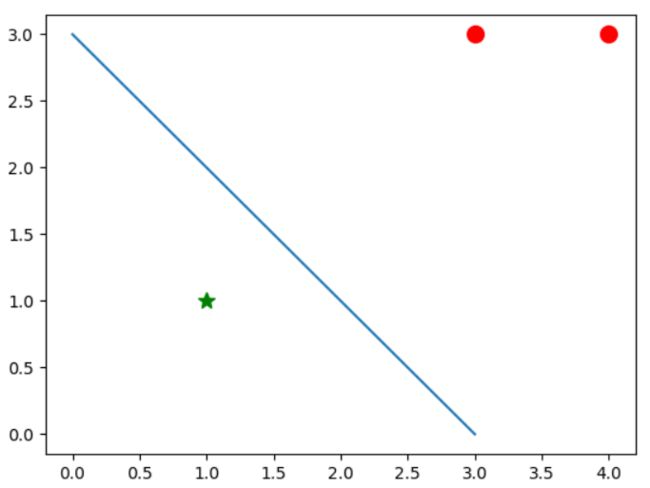
可以看出此超平面实现了对点的二分类，当然，我们可以使用随机梯度下降方法来进行分类，得到的一种结果为w=[2 1]，b=-5，其结果图如下：

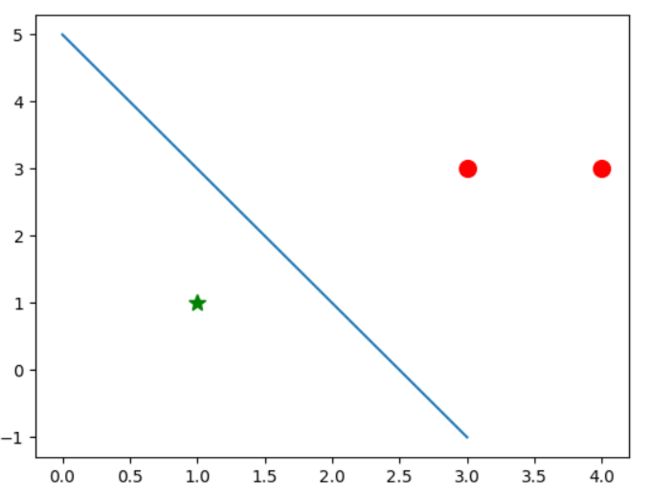
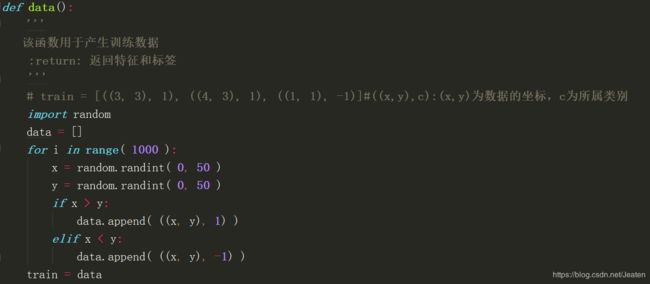
接下来，我们构造一个二分类的数据集来看看分类的效果，构造数据集的时候可将产生数据集的“train=”部分用以下或别的函数代替。笔者使用了随机产生1000个数的方法，产生代码如下：

import random
data = []
for i in range( 1000 ):
    x = random.randint( 0, 50 )
    y = random.randint( 0, 50 )
    if x > y:
        data.append( ((x, y), 1) )
    elif x < y:
        data.append( ((x, y), -1) )
train=data

产生方法如下：

我们使用随机梯度下降的方法进行二分类，得到一组参数为：w=[72 -72]，b=-1，分类结果如下图所示：

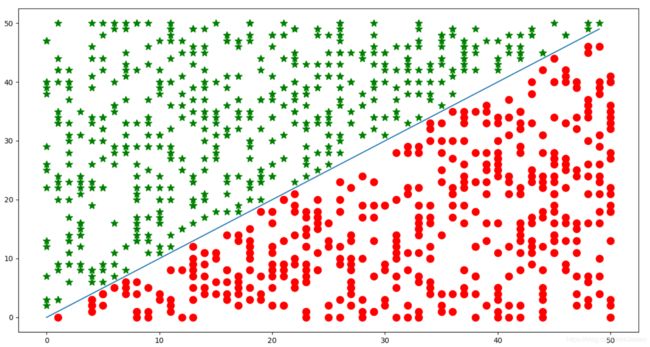
可以看出分类效果还是很不错的。
以上就是本期的感知机的原理和python的代码实现，欢迎交流批评指正！

创作不易，觉得写得不错就微信扫码奖励一下吧！