机器学习 | 聚类 —— FCM模糊聚类算法
1.FCM模糊聚类原理
模糊c均值聚类FCM算法融合了模糊理论的精髓,相较于k-means的硬聚类,FCM算法(Fuzzy C-Means,FCM)提供了更加灵活的聚类结果。因为大部分情况下,数据集中的对象不能划分成为明显分离的簇,将一个对象划分到一个特定的簇有些生硬,不符合人的客观认知。因此,对每个对象和每个簇赋予一个权值,指明对象属于该簇的程度即可。当然,基于概率的方法也可以给出这样的权值,但是有时候我们很难确定一个合适的统计模型,因此使用具有自然地、非概率特性的FCM聚类算法就是一个比较好的选择。
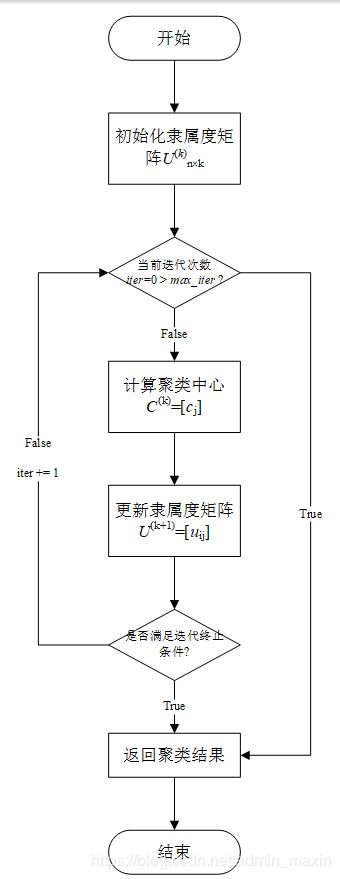
2.FCM模糊聚类流程
3.FCM模糊聚类程序
from pylab import *
from numpy import *
import pandas as pd
import numpy as np
import operator
import math
import matplotlib.pyplot as plt
import random
# 数据保存在.csv文件中
df_full = pd.read_csv("iris.csv")
columns = list(df_full.columns)
features = columns[:len(columns) - 1]
# class_labels = list(df_full[columns[-1]])
df = df_full[features]
# 维度
num_attr = len(df.columns) - 1
# 分类数
k = 3
# 最大迭代数
MAX_ITER = 100
# 样本数
n = len(df) # the number of row
# 模糊参数
m = 2.00
# 初始化模糊矩阵U
def initializeMembershipMatrix():
membership_mat = list()
for i in range(n):
random_num_list = [random.random() for i in range(k)]
summation = sum(random_num_list)
temp_list = [x / summation for x in random_num_list] # 首先归一化
membership_mat.append(temp_list)
return membership_mat
# 计算类中心点
def calculateClusterCenter(membership_mat):
cluster_mem_val = zip(*membership_mat)
cluster_centers = list()
cluster_mem_val_list = list(cluster_mem_val)
for j in range(k):
x = cluster_mem_val_list[j]
xraised = [e ** m for e in x]
denominator = sum(xraised)
temp_num = list()
for i in range(n):
data_point = list(df.iloc[i])
prod = [xraised[i] * val for val in data_point]
temp_num.append(prod)
numerator = map(sum, zip(*temp_num))
center = [z / denominator for z in numerator] # 每一维都要计算。
cluster_centers.append(center)
return cluster_centers
# 更新隶属度
def updateMembershipValue(membership_mat, cluster_centers):
# p = float(2/(m-1))
data = []
for i in range(n):
x = list(df.iloc[i]) # 取出文件中的每一行数据
data.append(x)
distances = [np.linalg.norm(list(map(operator.sub, x, cluster_centers[j]))) for j in range(k)]
for j in range(k):
den = sum([math.pow(float(distances[j] / distances[c]), 2) for c in range(k)])
membership_mat[i][j] = float(1 / den)
return membership_mat, data
# 得到聚类结果
def getClusters(membership_mat):
cluster_labels = list()
for i in range(n):
max_val, idx = max((val, idx) for (idx, val) in enumerate(membership_mat[i]))
cluster_labels.append(idx)
return cluster_labels
def fuzzyCMeansClustering():
# 主程序
membership_mat = initializeMembershipMatrix()
curr = 0
while curr <= MAX_ITER: # 最大迭代次数
cluster_centers = calculateClusterCenter(membership_mat)
membership_mat, data = updateMembershipValue(membership_mat, cluster_centers)
cluster_labels = getClusters(membership_mat)
curr += 1
print(membership_mat)
return cluster_labels, cluster_centers, data, membership_mat
def xie_beni(membership_mat, center, data):
sum_cluster_distance = 0
min_cluster_center_distance = inf
for i in range(k):
for j in range(n):
sum_cluster_distance = sum_cluster_distance + membership_mat[j][i] ** 2 * sum(
power(data[j, :] - center[i, :], 2)) # 计算类一致性
for i in range(k - 1):
for j in range(i + 1, k):
cluster_center_distance = sum(power(center[i, :] - center[j, :], 2)) # 计算类间距离
if cluster_center_distance < min_cluster_center_distance:
min_cluster_center_distance = cluster_center_distance
return sum_cluster_distance / (n * min_cluster_center_distance)
labels, centers, data, membership = fuzzyCMeansClustering()
print(labels)
print(centers)
center_array = array(centers)
label = array(labels)
datas = array(data)
# Xie-Beni聚类有效性
print("聚类有效性:", xie_beni(membership, center_array, datas))
xlim(0, 10)
ylim(0, 10)
# 做散点图
fig = plt.gcf()
fig.set_size_inches(16.5, 12.5)
f1 = plt.figure(1)
plt.scatter(datas[nonzero(label == 0), 0], datas[nonzero(label == 0), 1], marker='o', color='r', label='0', s=10)
plt.scatter(datas[nonzero(label == 1), 0], datas[nonzero(label == 1), 1], marker='+', color='b', label='1', s=10)
plt.scatter(datas[nonzero(label == 2), 0], datas[nonzero(label == 2), 1], marker='*', color='g', label='2', s=10)
plt.scatter(center_array[:, 0], center_array[:, 1], marker='x', color='m', s=30)
plt.show()