两种常见的点云配准方法ICP&NDT

迭代最近点算法ICP(Iterative Closest Point)

问题描述

  假设我们有两组点集，注意这里的$\mathbf{P}$和$\mathbf{Q}$分别相对于变换前和变换后的相机参考系。我们要解决的问题是找一组$\mathbf{R}$和$\mathbf{T}$，使得$\mathbf{P}$中的每一个点经过变化后同$\mathbf{Q}$中的最近点的误差之和最小。用数学的话描述就是最小化如下一个目标函数：
$$\frac{1}{2}\sum _{i=1}^n\Vert {\mathbf{q}}_i-\mathbf{R}{\mathbf{p}}_i-\mathbf{T}{\Vert }^2\text{\hspace{1em}(1.1)}$$
求解的方法有很多，这里只介绍SVD方法

目标函数简化

我们定义两组点集的中心为
$${\mu }_p=\sum _{i=1}^n{\mathbf{p}}_i\text{\hspace{1em}(1.2)}$$
$${\mu }_q=\sum _{i=1}^n{\mathbf{q}}_i\text{\hspace{1em}(1.3)}$$
$$\begin{gathered} \Vert {\mathbf{q}}_i-\mathbf{R}{\mathbf{p}}_i-\mathbf{T}{\Vert }^2=\Vert {\mathbf{q}}_i-\mathbf{R}{\mathbf{p}}_i-\mathbf{T}-({\mu }_q-\mathbf{R}{\mu }_p)+({\mu }_q-\mathbf{R}{\mu }_p){\Vert }^2 \\ =\Vert {\mathbf{q}}_i-{\mu }_q-\mathbf{R}({\mathbf{p}}_i-{\mu }_p)+({\mu }_q-\mathbf{R}{\mu }_p-\mathbf{T}){\Vert }^2 \\ =\Vert {\mathbf{q}}_i-{\mu }_q-\mathbf{R}({\mathbf{p}}_i-{\mu }_p){\Vert }^2+\Vert {\mu }_q-\mathbf{R}{\mu }_p-\mathbf{T}{\Vert }^2+2({\mathbf{q}}_i-{\mu }_q-\mathbf{R}({\mathbf{p}}_i-{\mu }_p){)}^T({\mu }_q-\mathbf{R}{\mu }_p-\mathbf{T}) \end{gathered}$$
注意到最后一项
$$\begin{gathered} \sum _{i=1}^n({\mathbf{q}}_i-{\mu }_q-\mathbf{R}({\mathbf{p}}_i-{\mu }_p){)}^T({\mu }_q-\mathbf{R}{\mu }_p-\mathbf{T}) \\ =({\mu }_q-\mathbf{R}{\mu }_p-\mathbf{T}{)}^T\sum _{i=1}^n({\mathbf{q}}_i-{\mu }_q-\mathbf{R}({\mathbf{p}}_i-{\mu }_p)) \\ =({\mu }_q-\mathbf{R}{\mu }_p-\mathbf{T}{)}^{T}0=0 \end{gathered}$$
从而原式可化简为
$$\frac{1}{2}(\sum _{i=1}^n\Vert {\mathbf{q}}_i^{\prime }-\mathbf{R}{\mathbf{p}}_i^{\prime }{\Vert }^2+\Vert {\mu }_q-\mathbf{R}{\mu }_p-\mathbf{T}{\Vert }^2)\text{\hspace{1em}(1.4)}$$
其中${\mathbf{q}}_i^{\prime }={\mathbf{q}}_i-{\mu }_q$ ，${\mathbf{p}}_i^{\prime }={\mathbf{p}}_i-{\mu }_p$
该目标函数的最优解求解可以分为两部分，先求第一项，再求第二项（实际上第二项最优解始终为0）
$$\begin{gathered} \Vert {\mathbf{q}}_i^{\prime }-\mathbf{R}{\mathbf{p}}_i^{\prime }{\Vert }^2=({\mathbf{q}}_i^{\prime }-\mathbf{R}{\mathbf{p}}_i^{\prime }{)}^T({\mathbf{q}}_i^{\prime }-\mathbf{R}{\mathbf{p}}_i^{\prime }) \\ =({\mathbf{q}}_i^{\prime T}{\mathbf{q}}_i^{\prime }+{\mathbf{p}}_i^{\prime T}{\mathbf{R}}^T\mathbf{R}{\mathbf{p}}_i^{\prime }-2{\mathbf{q}}_i^{\prime T}\mathbf{R}{\mathbf{p}}_i^{\prime }) \\ =({\mathbf{q}}_i^{\prime T}{\mathbf{q}}_i^{\prime }+{\mathbf{p}}_i^{\prime T}{\mathbf{p}}_i^{\prime }-2{\mathbf{q}}_i^{\prime T}\mathbf{R}{\mathbf{p}}_i^{\prime })\text{\hspace{1em}(1.5)} \end{gathered}$$
即最小化目标函数等价于最大化${\sum }_{i=1}^n{\mathbf{q}}_i^{\prime T}\mathbf{R}{\mathbf{p}}_i^{\prime }$

SVD求解

在上一步的基础上，有
$$\sum _{i=1}^n{\mathbf{q}}_i^{\prime T}\mathbf{R}{\mathbf{p}}_i^{\prime }=Tr(\sum _{i=1}^n\mathbf{R}{\mathbf{p}}_i^{\prime T}{\mathbf{q}}_i^{\prime })\triangleq Tr(\mathbf{R}\mathbf{H})\text{\hspace{1em}(1.6)}$$
引理1：对任意正定对称阵$A{A}^T$和任意正交阵$B$，有
$$Tr(A{A}^T)\ge Tr(BA{A}^T)\text{\hspace{1em}(1.7)}$$
这个引理用Schwarz不等式很容易得到，不在这里证明了。
我们的目的是什么呢？根据(1.6)，我们的目的是要找一个$R$使得$Tr(RH)$最大。那由上面这个引理，我们很容易想到，如果$RH$是一个对称正定的形式，那对任何旋转矩阵$R$，显然迹只会不增。因此我们对$H$做SVD分解，$H=U\Lambda V^T$，那么$X=V{U}^T$就是我们要找的$R$。因为
$$XH=V{U}^{T}U\Lambda V^T=V\Lambda V^T\text{\hspace{1em}(1.8)}$$是正定对称阵，则由引理1可知，对任意旋转矩阵（正交）$B$，都有$$Tr(XH)\ge Tr(BXH)\text{\hspace{1em}(1.9)}$$即$X$是使得(1.6)式最大的$R$。

迭代过程

实际上刚才我们只完成了一次计算，而ICP的全称是Iterative Closest Point，即迭代最近点。我们来理解一下整个过程

1. 对P中的每个点，在Q中找到匹配的最近点。这里需要注意，并不是每次的点云都是一一匹配，点云的数量是一方面，另外可以预见的是，很容易出现多对一最近点匹配，当然，可以通过一些额外的限定在达到一对一匹配的效果。
2. 根据上述过程计算最优的R和T.
3. 利用得到的位姿作用于P，如果此时的误差大于阈值，则重新进行迭代，直到迭代次数达到阈值或者误差小于阈值。

简单的理解，有点像梯度下降寻找极值点的过程，同样的，一个好的初值对加快ICP的收敛过程也十分重要。另外点对点的计算量十分大，复杂度为$O(mn)$，在一维的情况下，二分查找是常见的优化，对高维的情况，一个类似的过程是通过KD树来实现的。

KD树优化匹配过程

KD树原理

KD树是每个节点均为K维数值的二叉树，其上的每个节点代表一个超平面，该超平面垂直于当前划分维度的坐标轴，并在该维度上将空间一分为二。其构建过程是循环选取数据点的各个维度来作为切分维度，将当前维度的中值作为划分点，递归处理各子树，直到所有数据点挂载完毕。

KD树的一些优化

切分维度选择的时候，一般优先选择方差大的维度开始切分。
选择中值时，对数据量较大的维度，不一定严格取中值，可以随机采样一定的数据，并取采样的中值作为划分点，加快划分过程。

一个例子

以二维平面点(x,y)的集合(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)为例结合下图来说明k-d tree的构建过程。

对应的是将一个二维平面逐步划分的过程

KD树最近邻搜索过程

我们构建KD树的目的是为了加快最近点搜索过程，那么KD树如何进行最近邻搜索呢？
假设我们要搜索同（3,5）最近的点。
1）从根节点（7,2）出发，将当前的最近邻设为（7,2），对KD树做深度优先遍历。以（3,5）为圆心，到（7,2 ）的距离为半径画圆。对在圆外的点，如果位于左侧，则忽略左子树，位于右侧，则忽略右子树。下图忽略（8,1）的右子树。
2）深度遍历子节点。以（5,4）为根节点，判断（5,4）比（7,2）更近，更换最近点，并重新剪枝。此时，（7,2）的右子树均被忽略。
3）深度遍历子节点，直到遍历结束，返回最近点。

完整伪代码如下图

KD树构建的复杂度为$O(log(m))$，查找的复杂度为$O(mlog(n))$，所以利用KD查找最近邻的复杂度为$O(mlog(n))$，远小于$O(mn)$。

正态分布变换NDT(Normal Distribution Transform)

简介

目前的配准方法，前提都是环境大部分是不变的，但是完全不变的环境其实也是很少的，比如一辆车飞驰而过，一个人走过等。我们更多应该考虑的是允许小部分差异的配准，这时候点对点匹配比如ICP就会出现一些问题，而NDT则可以很好地解决细微差。
我们知道，如果随机变量满足正态分布，那么对应的概率密度函数（PDF）为
$$p(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$
对随机向量则有
$$p(x)=\frac{1}{(2\pi {)}^{\frac{D}{2}}\sqrt{|\mathbf{\Sigma }|}}{e}^{-\frac{(x-{\mu )}^T{\mathbf{\Sigma }}^{-1}(x-\mu )}{2{\sigma }^2}}$$
其中D表示维数，$\mathbf{\Sigma }$表示协方差矩阵。简单来说，一维的数变成了高维的向量。

目标函数

与ICP不同，NDT假设点云服从正态分布，我们的目的是找一个姿态，使得当前扫描点位于参考扫描平面上的可能性最大。假设当前扫描得到的点云为$X=\{x_1,x_2,...,x_n\}$，用空间转换函数$T(p,x)$来表示使用姿态变换$p$来移动$x$。我们的目标是最大化似然函数：
$$\theta =\prod _{k=1}^{n}p(T(p,x))$$
等价于最小化负对数似然，这么做还有一个好处，加法对求导更友好
$$-\log \theta =-\sum _{k=1}^n\log p(T(p,x)$$

基本步骤

在上一部分中我们没有解释p函数，当然你可能会说不就是概率密度函数吗？是，但是我们并没有先验的概率密度函数，怎么得到的。这里唯一可以利用的即使参考点云，我们将参考点云网格化，然后计算每个网格的多维正态分布参数。用$y_k=1,2,...,m$表示一个网格内的所有扫描点，则
均值：$\mu =\frac{1}{m}{\sum }_{k=1}^m{y}_k$
协方差矩阵：$\Sigma =\frac{1}{m}{\sum }_{k=1}^m(y_k-{\mu }_k)(y_k-{\mu }_k{)}^T$
概率密度函数：$p(x)=\frac{1}{(2\pi {)}^{\frac{3}{2}}\sqrt{|\mathbf{\Sigma }|}}{e}^{-\frac{(x-{\mu )}^T{\mathbf{\Sigma }}^{-1}(x-\mu )}{2}}$
实际上这里f不是正态分布也可以
下一步就是如何求解

对目标函数进行数学上的简化

如下图所示，直接取负对数会出现无穷大的点，这样偶然扫到的一些异常点可能会对本来表现很好的结果产生很大的影响导致被舍弃，为了避免这种情况，在原函数的基础上做了一些限制。
$\overline{p}(x)=c_{1}exp(-\frac{(x-{\mu )}^T{\mathbf{\Sigma }}^{-1}(x-\mu )}{2})+c_2{p}_0$

这时候我们的目标函数中的单项就变成
$$-\log (c_{1}exp(-\frac{(x-\mu {)}^T{\mathbf{\Sigma }}^{-1}(x-\mu )}{2})+c_2)$$
我们之前也提到了，加法对求导比较友好，但是log函数对求导不友好，而在求解优化问题的时候，经常会利用到一阶二阶导数（比如梯度下降，牛顿法），所以我们想办法对上述函数做一个近似，如果你对函数图像有一定的敏感性的化，很容易发现上面这两个绿色的函数好像还挺像？也就是说我们可以利用高斯函数来拟合负对数
$$p(x)=d_{1}exp(-d_2\frac{(x-\mu {)}^T(x-\mu )}{2{\sigma }^2})+d_3$$
$$\overline{p}(x)=-\log (c_{1}exp(-\frac{(x-\mu {)}^T(x-\mu )}{2{\sigma }^2})+c_2)$$
利用x=0，$\sigma$，$\infty$解得近似参数为
$d_3=-\log (c_2)$
$d_1=-\log (c_1+c_2)-d_3$
$d_2=-2\log ((-\log (c_{1}exp(-1/2)+c_2)-d_3)/d_1)$
这样，我们可以得到不同项对NDT结果的贡献（偏移项是一致的，可暂时忽略），注意这里多了一个负号，我的理解应该是为了之后求导时前面的负号正好可以消掉
$$p(x_k)=-d_{1}exp(-d_2\frac{(x_k-{\mu }_k{)}^T{\mathbf{\Sigma }}_k^{-1}(x-{\mu }_k)}{2})$$
原目标函数变成
$$s(p)=-\sum _{k=1}^{n}p(T(p,x_k))$$

牛顿法求解

这公式实在长，直接截图了，牛顿法的关键就是通过梯度矩阵g和海森矩阵H求解步长

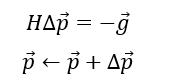
这里对上面的结果求导可得

举一个简单的二维的例子来说明上面的$x_k$对$p_i$的求导过程

最后结合流程图梳理一下NDT的流程

1）划分网格
2）计算各网格的PDF
3）对每个点云数据，找到对应的网格点，并根据PDF和评分函数计算结果
4）根据结果更新g和H，计算新的步长
5）判断是否收敛或达到迭代次数，是则跳出，否则继续步骤3-5

对NDT实验结果的一些优化

1. cell size. 太大了容易导致损失一些局部特征，太小了则会增加很多计算量，太小会导致失去统计普适性，部分数据对结果影响过大。另外，作者直接舍弃掉少于五个数据的网格（因为会造成协方差矩阵不可逆）。
2. Fixed discretization。固定大小是最常见的划分方式，操作简单，而且容易找到每个点对应的网格。缺点的话见底下几种方法
3. Octree discretization。如何快速找到每个点对应的网格是搜索速度的关键，八叉树结构是常见的三维搜索树。
4. Iterative discretization。好的初始位置可以加快收敛过程，一个常见的方法就是起始位置迭代，将上一次的终点位姿作为本次的起点位姿
5. Adaptive clustering。非固定大小网格划分的一种方法，采用K均值聚类（其他聚类方式类似）划分，更能表现出每个局部数据的特征。
6. Linked cells。上面提到数据少于五的网格会被舍弃，导致会出现一些空网格，损失了一些完整性，一个改进措施是将这些空网格用指针连接到最近的非空网格上，以该处的PDF代替，由于处于边缘，值还是很小，但是保证了数据的完整性。
7. Trilinear interpolation。插值的逻辑就是固定划分实际上会出现边缘不连续的情况，插值法相当于做了一个平滑，计算的时候考虑所有含该数据点的网格取最优值，计算量大约是原来的4倍，但效果也有较大的改善。示意图如下
   

其他一些配准方法

1. Iterative dual correspondences (IDC) algorithm。ICP的一种改进，主要是采用极坐标代替笛卡尔坐标系进行最近点搜索
2. Probabilistic iterative correspondence (PIC) method。这个方法考虑了噪声和初始位姿的不确定性
3. Gaussian fields。采用高斯混合模型，类似NDT
4. Conditional random fields (CRFs) 。条件随机场，还没细看
5. Branch-and-bound strategy 。分支定界法，没看。
6. Registration using local geometric features。结合图像的局部特征进行匹配
7. 除此之外最近还有一些结合深度学习的方法，比如百度无人车团队2019CVPR的工作：L3-Net: Towards Learning based LiDAR Localization for Autonomous Driving。输入包括实时激光点云，地图和IMU数据，输出位姿结果。

参考资料

1.ICP SVD方法论文： Least-Squares Fitting of Two 3-D Point Sets
2. NDT方法详细介绍论文：Magnusson M. The three-dimensional normal-distributions transform: an efficient representation for registration, surface analysis, and loop detection[D]. Örebro universitet, 2009.
3. 论文2部分翻译：https://blog.csdn.net/qq_23225073/article/details/89221098
4. KD树介绍：https://leileiluoluo.com/posts/kdtree-algorithm-and-implementation.html