leetcode 经典栈相关题目(思路、方法、code)

用于回顾数据结构与算法时刷题的一些经验记录
栈的题目还是稍微有些难度的

20. 有效的括号

给定一个只包括 ‘(’，’)’，’{’，’}’，’[’，’]’ 的字符串，判断字符串是否有效。

有效字符串需满足：

• 左括号必须用相同类型的右括号闭合
• 左括号必须以正确的顺序闭合
• 注意空字符串可被认为是有效字符串

示例 1:
输入: "()"
输出: true
示例 2:
输入: "()[]{}"
输出: true

分析：判断括号是否有效是栈的最经典的运用之一。一个括号序列有效，需要对于每一个左括号都要有相应的右括号对应，还需要有相应的顺序才行。因此，如果一个右括号和之前输入的左括号相邻且匹配，则可以将其消去

因此在这里用栈作为数据结构解答该题，设置一个栈，如果加入的是一个左括号，则将其加入，如果加入的是一个右括号，则判断其是否能够与栈顶的括号对应，如果对应，则将栈顶 pop ，否则说明有错。因此经过对字符串的处理，如果最终栈不是空的，说明该字符串不是有效字符串。

class Solution {
public:
    bool isValid(string s) 
	{
    	stack<char> st;
		for(int i=0;i<s.size();i++)
		{
			if(s[i]=='('||s[i]=='{'||s[i]=='[') //左括号加入
				st.push(s[i]);
			else if(st.size()>0&&(s[i]==')'&&st.top()=='('||s[i]==']'&&st.top()=='['||s[i]=='}'&&st.top()=='{'))//右括号需要判断能否消除,不能消除即出错
				st.pop();
			else
				return false;	
		}
		if(st.size()==0)
			return true;
		return false;    
    }
};

155. 最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。

分析：通常的栈结构，push,pop,top均可以满足，但是 getMin()不能满足，能否增添一个变量用来标记最小值？如果有这个变量，则每次push元素我们都可以将元素进行比较，这样就可以O(1)获取最小元素。但是仔细想想，如果将最小元素pop了出来，那么现在的最下元素怎样标记？只能遍历获得，因此最终是O(n)获取最小元素。

故需要转换思路，怎样才能动态地存取最小元素？采用辅助栈。

使用两个栈，一个栈作为正常栈，另一个栈作为辅助栈。辅助栈用来存取当前的最小值，如果最小值更新，则压入新的最小值即可。

例子：

入栈 3 
|   |    |   |
|   |    |   |
|_3_|    |_3_|
stack  minStack

入栈 5 ,5大于minStack的栈顶，故不压入
|   |    |   |
| 5 |    |   |
|_3_|    |_3_|
stack  minStack

入栈 2 ，2小于最小值栈的栈顶，故将其入栈
| 2 |    |   |
| 5 |    | 2 |
|_3_|    |_3_|
stack  minStack

出栈 2，发现2是最小栈的栈顶，故minStack也出栈
|   |    |   |
| 5 |    |   |
|_3_|    |_3_|
stack  minStack

出栈 5，发现5不是最小栈的栈顶，因此minStack 不处理
|   |    |   |
|   |    |   |
|_3_|    |_3_|
stack  minStack

注意：如果入栈元素小于等于最小栈栈顶，则将其入栈，而非仅考虑小于，这是为了避免pop时候出错。(应对连续的相同元素)

class MinStack {
	private:
		stack<int> data;
		stack<int> min;
public:
    /** initialize your data structure here. */
    MinStack() 
	{
        
    }
    
    void push(int x) 
	{
        data.push(x);
		if(!min.empty()&&x<=min.top()) //最小栈不是空且最小栈栈顶元素小于等于x，则入栈 
			min.push(x); 
		if(min.empty()) //最小栈为空 
        	min.push(x);
    }
    void pop() 
	{
		if(data.top()==min.top()) //如果要pop的元素等于最小栈栈顶，则将其pop 
			min.pop();
		data.pop();   
    }
    
    int top() 
	{
      return data.top();  //返回data的栈顶即可  
    }
    
    int getMin() 
	{
        return min.top(); //返回min的栈顶即可 
    }
};

946. 验证栈序列

给定 pushed 和 popped 两个序列，每个序列中的 值都不重复，只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时，返回 true；否则，返回 false 。

示例 1：
输入：pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出：true
解释：我们可以按以下顺序执行：
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1

示例 2：
输入：pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出：false
解释：1 不能在 2 之前弹出。

分析：验证栈序列是否合法也是比较经典的栈相关题目。

首先思考为什么会出现不合法序列，主要是因为有些元素在特定上课并不是在栈顶但pop出了。

使用栈来模拟该过程。每次将pushed序列向模拟栈中加入一个元素，每加入一个元素，都要判断是否与当前popped序列当前的输出位置元素相同，如果相同，则将栈目前元素pop处，popped序列位置右移(注意这里是用一个循环，如果top的内容与popped序列位置内容一致则一直pop()。最终如果是合法序列的话最后的栈应该是空的，否则说明非法。

class Solution {
public:
    bool validateStackSequences(vector<int>& pushed, vector<int>& popped) 
    {
		stack<int> S;
		int length=pushed.size();
		int j=0;
		for(int i=0;i<length;i++)
		{
			S.push(pushed[i]);
			while(!S.empty()&&S.top()==popped[j]) //每次push后都要将能消除的消除了	
			{
				S.pop();
				j++;
			}
		}
		if(!S.empty())
			return false;
		return true; 
    }
};

单调栈：

单调栈是比较特殊的栈结构，分为单调递增栈和单调递减栈，即从栈底元素到栈顶元素呈单调递增或单调递减，栈内序列满足单调性的栈；

以单调递增栈为例，实现方式为：

• 如果新的元素比栈顶元素小，则出栈，直至栈顶元素小于新的元素
• 如果新的元素比栈顶元素大，则入栈

以该方式形成的栈，栈内会是递增的，且当元素出栈的时候，说明要加入的元素是该元素向后找到的第一个比它小的元素

单调栈用来解决下一个更大(更小)的元素相关问题，可以在O(n)时间内解决

496. 下一个更大元素 I

给定两个 没有重复元素 的数组 $nums1$ 和 $nums2$ ，其中$nums1$ 是 $nums2$ 的子集。找到 $nums1$ 中每个元素在 $nums2$ 中的下一个比其大的值。

$nums1$ 中数字 x 的下一个更大元素是指 $x$ 在 $nums2$ 中对应位置的右边的第一个比 $x$ 大的元素。如果不存在，对应位置输出 $-1$ 。

示例 1:
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
    对于num1中的数字4，你无法在第二个数组中找到下一个更大的数字，因此输出 -1。
    对于num1中的数字1，第二个数组中数字1右边的下一个较大数字是 3。
    对于num1中的数字2，第二个数组中没有下一个更大的数字，因此输出 -1。

分析：这里需要注意的是**，$nums1$是$nums2$的子集**，因此，如果我们找到了$num2$中每个元素的下一个更大的元素，则可以堆$nums1$直接遍历即可获得结果序列。

大致思路：

• 建立递减栈，对 $nums2$ 中元素遍历，将元素依次放入递减栈，如果放入过程中，需要pop，则说明该元素是需要被pop出元素的下一个更大的数字，此时建立一个映射map，将该关系存入map中，遍历结束后，如果栈中还有元素，则将其pop出，且其对应的map值为-1，表示其后面没有比它更大的元素
• 对 $nums1$ 中的元素依次取map中对应的匹配即可

class Solution {
public:
    vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) 
	{
		stack<int> min_stack;
		map<int,int> HASH;
		for(int i=0;i<nums2.size();i++)
		{
			while(!min_stack.empty()&&min_stack.top()<nums2[i])  //将小于num2[i]的元素pop出且建立映射 
			{
				HASH[min_stack.top()]=nums2[i];
				min_stack.pop();
			}
			min_stack.push(nums2[i]);
		}
		while(!min_stack.empty()) //对于栈中剩余元素建立映射
		{
			HASH[min_stack.top()]=-1;
			min_stack.pop();
		}
		vector<int> result;
		for(int i=0;i<nums1.size();i++)  //遍历取映射即可
			result.push_back(HASH[nums1[i]]);
		return result;
    }
};

503. 下一个更大元素 II

给定一个循环数组（最后一个元素的下一个元素是数组的第一个元素），输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1。

示例 1:
输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

分析：还是利用单调栈的方法，因为数组是循环的，实际上也不需要让它循环，只需要遍历两边即可(可以物理地复制数组使其增倍，也可以利用巧妙利用数学关系两次遍历)

实践中发现，如果从后往前遍历的话，对于结果的存储会更方便。

• 利用数学关系将数组等价于扩充2倍
• 从后往前遍历，如果一个数字小于当前栈顶，则加入，且将该数字对应的坐标的ans设置为栈顶元素。如果该数字大于栈顶元素，则栈顶元素pop出，直至为空或栈顶大于该元素，然后将该元素加入栈

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) 
	{
		int length=nums.size();
		vector<int> ans(length);  //存结果
		stack<int> min_stack;   //作为递减栈
		for(int i=2*length-1;i>=0;i--)
		{
			while(!min_stack.empty()&&min_stack.top()<=nums[i%length]) //注意这里需要有等号
			{
				min_stack.pop();	
			}
			ans[i%length]=min_stack.empty()?-1:min_stack.top(); 
			min_stack.push(nums[i%length]);	
		}
		return ans; 
    }
};

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

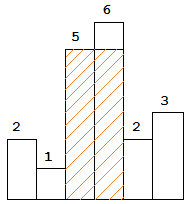
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

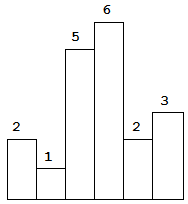
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

分析：如何求一个对应高度的对应矩形的面积？实际上，就是要找到这个高度对应的左侧比它低的地方，右侧比它低的地方，然后就可以确定处以该位置的高度作为矩形的宽度。

(做该题一定要画图找到关系！)

因此既然是找下一个更大或者更小元素，因此单调栈便可以派上用场。

我在处理该题过程中遇到了较多的麻烦。起初不知道如何将宽度存储，然后我想到了用pair来存储每一个坐标和它对应的高度，当然是可行的，但是仔细一想，既然有了坐标，那它对应的高度便可以直接用数组来求呀，因此，实际上坐标已经蕴含了<坐标，高度>这一概念。因此在建立单调栈时，虽然采用的是高度进行判断，但是栈内存储的内容是坐标。然后第二个问题，一些情况下栈最后也不是空的，因此还需要特殊处理，在此我采用了哨兵节点，可以在高度的数组最前端和最后端分别加上一个0，这样既可以保证栈非空，且可以保证高度都会被计算。

• 维持的是递增栈，因此对于一个元素，在栈中其下的元素一定是前面的元素中离它最近的小于它的元素。
• 每次pop时均说明可以确定一个位置对应的高度对应的矩形面积了，求其值取最大即可。

参照：https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/zhao-liang-bian-di-yi-ge-xiao-yu-ta-de-zhi-by-powc/
对该题讲解的较为不错

class Solution {
public:
int largestRectangleArea(vector<int>& heights)
{
    int ans = 0;
    stack<int> max_stack;  // 
    heights.insert(heights.begin(), 0);
    heights.push_back(0); //加入两个哨兵节点 
    for (int i = 0; i < heights.size(); i++)
    {
        while (!max_stack.empty() && heights[max_stack.top()] > heights[i])
        {
            int cur = max_stack.top();
            max_stack.pop();
            int left = max_stack.top() + 1; //左部就是将当前的pop出去后的top下标，也就是向左延申的最远位置 
            int right = i;       //向右延申最远位置就是当前的i 
            ans = max(ans, (right - left) * heights[cur]);
        }
        max_stack.push(i);
    }
    return ans;
}
};