leetcode 经典回溯算法题目(思路、方法、code)
用于回顾数据结构与算法时刷题的一些经验记录
-
回溯与递归都要注意剪枝,避免重复计算
-
回溯的问题,一定要把整个树图画出来,然后再去考虑如何缩小问题,还要注意恢复状态
-
回溯算法的大致模板:
- 根据这个模板,然后根据自己画出的树图,基本所有回溯问题都可以搞定。
void backtrack(已经做的选择, 选择列表): if 当前达到了结束位置: result.push(最终的选择序列) for 每个选择 in 选择列表: 做选择 //可能这里需要判断选择是否可行 backtrack(新的已选择, 新的选择列表) //这里的已选择和选择列表都要更新 撤销选择 //在此基础上,如果部分节点已经无解,则将它能够推理出的无解的树枝均剪掉
文章目录
- [46. 全排列](https://leetcode-cn.com/problems/permutations/)
- [78. 子集](https://leetcode-cn.com/problems/subsets/)
- [90. 子集 II](https://leetcode-cn.com/problems/subsets-ii/)
- [39. 组合总和](https://leetcode-cn.com/problems/combination-sum/)
- [40. 组合总和 II](https://leetcode-cn.com/problems/combination-sum-ii/)
- [22. 括号生成](https://leetcode-cn.com/problems/generate-parentheses/)
- [77. 组合](https://leetcode-cn.com/problems/combinations/)
- [51. N皇后](https://leetcode-cn.com/problems/n-queens/)
- [52. N皇后 II](https://leetcode-cn.com/problems/n-queens-ii/)
46. 全排列
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
分析: 全排列的发现过程:
因此,每一步,我们需要确定一下当前深度的位置的元素,然后就可以继续向下展开。例如:如果在第一个位置选择了1,则在第二个位置可以选择2或者3,选择后再次选择第三个位置的元素。
如果在第i个位置选过后,则之后等价于前i个位置的元素排列已经确定,而后面实际上就是还没有排列的元素的全排列。这里就可以发现递归的思想。
因此回溯的大致思路为:
- 函数需要保存的内容有:当前已经确定的序列,当前的位置,序列的总长度
- 每次判断,是否已经遍历完,即当前位置是否等于序列的总长度,如果等于说明当前序列已经是一个结果,存储
- 如果没有遍历完,则确定一下该位置的元素,然后继续递归,递归时需要将当前位置右移
- 在这里确定元素时,可以用循环的方式直接确定,但是每次递归结束后,需要恢复现场,将状态均恢复,否则将导致回溯的难以结束或者结果不足
class Solution {
public:
vector<vector<int> > result;
vector<vector<int> > permute(vector<int>& nums)
{
backtrack(nums,0,nums.size());
return result;
}
void backtrack(vector<int>& output,int first,int len)
//output为当前已有的排列,first表示现在排列到的位置,len为长度
{
if(first==len)
{
result.emplace_back(output);
return ;
}
for(int i=first;i<len;i++) //进行回溯,每次确定好当前位置的元素后继续递归即可
{
swap(output[i],output[first]); //将目前的位置依次换成output[i]
backtrack(output,first+1,len);
swap(output[first],output[i]); //回溯的关键,在于递归后要恢复现场
}
}
};
78. 子集
给定一组不含重复元素的整数数组 n u m s nums nums,返回该数组所有可能的子集(幂集)。
**说明:**解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[[3],[1],[2],[1,2,3],[1,3],[2,3],[1,2],[]]
分析:
方法一:枚举或递归的思想
对于 n u m s nums nums 中每个元素,都有两种考虑,即选择或者不选择,因此最终结果数目是 2 n 2^n 2n ,时间复杂度也是 O ( n 2 n ) O(n2^n) O(n2n),因为每个结果都需要加到列表中,这是一个 O ( n ) O(n) O(n) 的复杂度
因此,整个问题将化为类似于决策树的思路,模拟的方法很多,但思想一致,复杂度为 O ( N ∗ 2 n ) O(N*2^n) O(N∗2n)
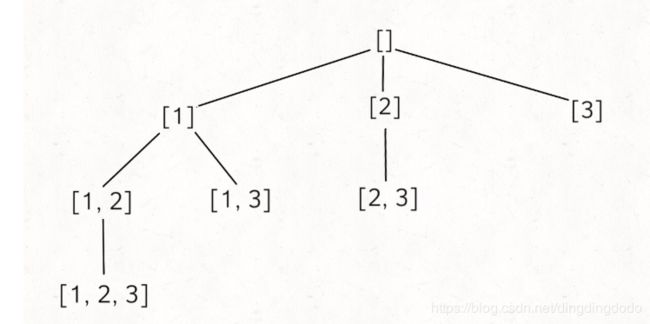
回溯法的思路更多地向该图所示,只要定好顺序,每次选择其中一个作为头,即可。这个过程也避免了繁重的剪枝
每次选择该节点或者不选择该节点,然后去回溯。
子集问题时,我们可以发现,该树中每一个节点都是结果,因此遍历到每一个节点都需要将其加入。
class Solution {
public:
vector<vector<int> > res;
vector<vector<int> > subsets(vector<int>& nums) {
vector<int> track; //记录走过的路径
backtrack(nums, 0, track);
return res;
}
void backtrack(vector<int>& nums, int start, vector<int>& track) //start记录位置
{
res.push_back(track); //每次把当前位置代表的子集加入result中即可
for (int i = start; i < nums.size(); i++) //在这里将选择不选择的思想化为以哪个位置开头
{
track.push_back(nums[i]); //将该位置的值放入到track
backtrack(nums, i + 1, track); //向下遍历,向自己的子节点进行遍历
track.pop_back(); //回溯回来后,将之前操作恢复,之后就走向自己的兄弟节点去遍历
}
}
};
90. 子集 II
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
**说明:**解集不能包含重复的子集。
分析:该问题,和上个问题几乎一样,只是可能包含重复元素,因此,如果对重复元素进行剪枝是该题的关键。
思路:我们将 n u m s nums nums 进行排序,按照上题思路,采用回溯法进行判断,但是,当做选择时,需要判断当前选择是否与之前做的一致,如果上一轮遍历时候做过该选择(也就是在树中表示的意思是该节点的左兄弟节点与子集一致),则不进行选择。
回溯的思想和顺序仍为下图,只是如果左兄弟节点和自身是一致时,则将该枝减去。

class Solution {
public:
vector<vector<int> > res;
vector<vector<int>> subsetsWithDup(vector<int>& nums)
{
vector<int> track; //记录走过的路径
sort(nums.begin(),nums.end());
backtrack(nums, 0, track);
return res;
}
void backtrack(vector<int>& nums, int start, vector<int>& track) //start记录位置
{
res.push_back(track); //每次把当前位置代表的子集加入result中即可
for (int i = start; i < nums.size(); i++)//在这里将选择不选择的思想化为以哪个位置开头
{
if(i==start||nums[i]!=nums[i-1])
//如果该节点是最左侧子节点或者与左侧节点不同的话,则正常向下遍历,否则取消这一轮的遍历
{
track.push_back(nums[i]); //将该位置的值放入到track
backtrack(nums, i + 1, track); //向下遍历,向自己的子节点进行遍历
track.pop_back(); //回溯回来后,将之前操作恢复,之后就走向自己的兄弟节点去遍历
}
}
}
};
39. 组合总和
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的数字可以无限制重复被选取。
- 所有数字(包括
target)都是正整数。 - 解集不能包含重复的组合。
示例:
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
分析:
首先对节点进行了排序,然后如果一个节点当前的和已经大于target,则说明其右方兄弟节点肯定不成立,故将右方全部剪枝。为了避免重复,每个节点向下延伸的值,只能是小于等于其的。
类似于之前的代码,补充模板即可。
class Solution {
public:
vector<vector<int> > res;
vector<vector<int>> combinationSum(vector<int>& candidates, int target)
{
sort(candidates.begin(),candidates.end());
vector<int> track;
backtrack(candidates,track,0,target);
return res;
}
bool backtrack(vector<int>& candidates,vector<int> track,int start,int target)
{
if(target<0)
return false;
if(target==0)
{
res.push_back(track);return false;
}
bool conti=true;
for(int i=start;i<candidates.size();i++)
{
if(conti==false) break; //conti为false说明子节点和右兄弟节点一定都不成立
track.push_back(candidates[i]);
conti=backtrack(candidates,track,i,target-candidates[i]);
track.pop_back();
}
return true;
}
};
40. 组合总和 II
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[ [1, 7], [1, 2, 5], [2, 6],[1, 1, 6] ]
分析:和上个题比较,candidates 中每个数字只能出现一次,实际上只需要在上题基础上,在选择的时候,我们减去了部分选择即可。当然这里还需要注意的是candidates 中数字可以重复,因此如果一开始对数组进行了排序,则将重复的部分也直接剪去即可。
class Solution {
public:
vector<vector<int> > res;
vector<vector<int>> combinationSum2(vector<int>& candidates, int target)
{
sort(candidates.begin(),candidates.end());
vector<int> track;
backtrack(candidates,track,0,target);
return res;
}
bool backtrack(vector<int>& candidates,vector<int> track,int start,int target)
{
if(target<0)
return false;
if(target==0)
{
res.push_back(track);return false; //右兄弟节点和子节点均不会成立
}
bool conti=true;
for(int i=start;i<candidates.size();i++)
{
if(i==start||candidates[i]!=candidates[i-1])//剪去重复的节点
{
if(conti==false) break; //conti为false说明子节点和右兄弟节点一定都不成立
track.push_back(candidates[i]);
conti=backtrack(candidates,track,i+1,target-candidates[i]);
track.pop_back();
}
}
return true;
}
};
22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
输入:n = 3
输出:[ "((()))", "(()())", "(())()", "()(())","()()()" ]
分析:(有效?因为只有一种括号且数量相同,因此只要在任意位置右括号前左括号大于右括号数量即合法)
最暴力的方法,生成所有可能的字符串,然后保留有效的。
显然很多结果在过程中就已经是无效的,因此采用回溯法,尽可能剪枝。
因此,形成决策树:(大致的树形结构为)
也就是在个节点,都可以选择左括号或者右括号,然后继续生成,直至用完。
限制条件(剪枝条件):
- 如果在某处右括号数量大于左括号数量,则说明已经非法,剪枝。
- 左括号和右括号数量至多n个
- 因为在字符串生成过程中已经判断是否非法,因此最终生成的字符串都是合法的
class Solution {
public:
vector<string> result;
vector<string> generateParenthesis(int n)
{
string a="";
backtrack(a,n,n);
return result;
}
void backtrack(string a,int left,int right)
{
if(left==0&&right==0) //字符串已经形成,则push
{
result.push_back(a);
return ;
}
if(left>0) //还可以选左括号
{
backtrack(a+'(',left-1,right);
}
if(right>0) //还可以选右括号
{
if(left>=right) return; //说明当前放置的右括号已经大于等于左括号,再放置则非法
else
backtrack(a+')',left,right-1);
}
}
};
77. 组合
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[ [2,4],[3,4],[2,3],[1,2],[1,3],[1,4],]
分析:该问题和组合总和问题基本一致,只是在这里判断条件是是否已经有k个数,如果数达到,则结束。否则就继续递归。
以 n = 4 , k = 2 n=4,k=2 n=4,k=2 为例:
因为不能重复且是有序的,所以就构成了如图所示的决策树
如果深度到达k,则该结果应存储。
- 如果一个节点可选择的数目小于还需要添加的数字的数目,则剪枝
- 每次选择的数字,需要比当前数字都要大
class Solution {
public:
vector<vector<int> > result;
vector<vector<int> > combine(int n, int k)
{
vector<int> track;
if(n<k) return result;
backtrack(track,0,k,n);
return result;
}
void backtrack(vector<int> track,int length,int k,int n)
{
if(length==k) //当前序列长度到达k,则加入到结果中,返回
{
result.push_back(track);
return;
}
if(length>0&&n-track[length-1]<k-length) //后面的节点数一定小于k-length,故该情况不可能有解,直接剪枝
return;
for(int i=(length==0?length:track[length-1]);i<n;i++)
{
track.push_back(i+1);
backtrack(track,length+1,k,n);
track.pop_back();
}
return ;
}
};
51. N皇后
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例:
输入: 4
输出: [
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。
分析:N皇后问题是非常经典的问题,也就是如何放置N个皇后在N*N的棋盘中,使其不攻击,皇后可以攻击同一行、同一列、左上左下右上右下四个方向的任意单位。
因此这也是一个排列问题,在这里可以认为决策树的每一层就是棋盘的一行,在每个节点所做的选择就是,在该行的某一列放置一个皇后。
因此基本思路为
- 首先对棋盘进行初始化
- 进行回溯,每一行做出一个选择,即将该位置的’.‘换位’Q’,做出选择后需要判断该选择是否非法,如果非法则直接返回即剪枝
- 如果可以到达第n行且仍合法,则说明该结果合理,存储
- 判断非法时,只需要判断列以及右上方和左上方就可以了,首先判断是否越界,没有越界的话判断是否已经存在皇后。可以用一个方向数组表示,这里由于只判断上方,故方向数组只处理列的变化即可
class Solution {
public:
vector<vector<string> > result; //存储结果
vector<vector<string> > solveNQueens(int n)
{
vector<string> map(n, string(n, '.')); //直接初始化为n行n列的点
backtrack(map,0,n);
return result;
}
bool isVaild(vector<string>& map, int row, int col) {
int n = map.size();
static const int dx[]={-1,0,1}; //标记col的三种变化
for(int i=1;i<=row;i++) //检测上方,左上方,右上方是否存在Q
{
int new_row=row-i;
for(int j=0;j<3;j++)
{
int new_col=col+i*dx[j];
if(new_col>=0&&new_col<n&&map[new_row][new_col]=='Q')
return false;
}
}
return true;
}
void backtrack(vector<string>&map,int pos,int n) //pos表示当前高度
{
if(pos==n) //已经到达决策树的最底端
{
result.push_back(map);
return;
}
for(int i=0;i<n;i++)
{
if(!isVaild(map,pos,i)) //如果在(pos,i)的位置放置Q不合理的话,剪枝
continue; //否则在该处放置Q进行回溯
map[pos][i]='Q';
backtrack(map,pos+1,n);
map[pos][i]='.'; //回溯回去时候需要恢复状态
}
}
};
52. N皇后 II
对于N皇后Ⅱ,只需要将结果进行修改即可,每次成立时候计数+1,不需要存储具体的值。
class Solution {
public:
int result; //存储结果
int totalNQueens(int n)
{
vector<string> map(n, string(n, '.')); //直接初始化为n行n列的点
backtrack(map,0,n);
return result;
}
bool isVaild(vector<string>& map, int row, int col) {
int n = map.size();
static const int dx[]={-1,0,1}; //标记col的三种变化
for(int i=1;i<=row;i++) //检测上方,左上方,右上方是否存在Q
{
int new_row=row-i;
for(int j=0;j<3;j++)
{
int new_col=col+i*dx[j];
if(new_col>=0&&new_col<n&&map[new_row][new_col]=='Q')
return false;
}
}
return true;
}
void backtrack(vector<string>&map,int pos,int n) //pos表示当前高度
{
if(pos==n) //已经到达决策树的最底端
{
result++;
return;
}
for(int i=0;i<n;i++)
{
if(!isVaild(map,pos,i)) //如果在(pos,i)的位置放置Q不合理的话,剪枝
continue; //否则在该处放置Q进行回溯
map[pos][i]='Q';
backtrack(map,pos+1,n);
map[pos][i]='.'; //回溯回去时候需要恢复状态
}
}
};