leetcode二叉搜索树经典题目(思路、方法、code)

二叉搜索树的简介

二叉搜索树是这样的二叉树：任意一个节点，其左儿子节点小于它，右儿子节点大于它

        4
       / \
      2   7
     / \
    1   3

因此，二叉搜索树的具有非常高效的查找、插入和删除操作。

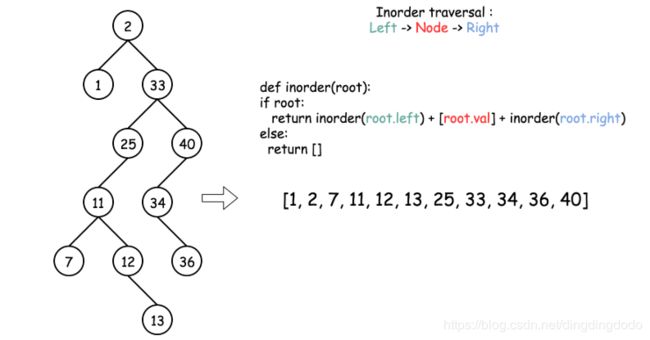
且，二叉搜索树的中序遍历，是一个递增的序列

98. 验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
• 节点的右子树只包含大于当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1:
输入:
    2
   / \
  1   3
输出: true
示例 2:

输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

分析：每个节点，需要大于左儿子节点的值，小于右儿子节点的值。且其左儿子和右儿子都是符合二叉搜索树的，很显然可以用递归解决。需要注意的是，右子树的所有节点的值必须都大于根节点，左子树的所有结点的值都必须小于根节点，因此需要设置一个辅助函数来限制范围。

• 空则true
• 该结点的值没有在限制的范围内，则返回false
• 否则返回两个子树的helper，需要更新子树的限制范围

class Solution {
public:
    bool helper(TreeNode* root, long long lower, long long upper) {
        if (root == NULL) return true;  //为空返回true
        if (root -> val <= lower || root -> val >= upper) return false;
        return helper(root -> left, lower, root -> val) && helper(root -> right, root -> val, upper);
    }
    bool isValidBST(TreeNode* root) {
        return helper(root, LONG_MIN, LONG_MAX);  //根没有限制
    }
};

700. 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 NULL。

例如，
给定二叉搜索树:

        4
       / \
      2   7
     / \
    1   3

值: 2
你应该返回如下子树:

      2     
     / \   
    1   3
在上述示例中，如果要找的值是 5，但因为没有节点值为 5，我们应该返回 NULL。

分析：二叉搜索树的搜索是最基础的应用，如果要搜的结点值小于当前结点，则向左走，否则向右走，直至找到或者为空。

//递归方式
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) 
    {
        if(root==NULL) return NULL;
        if(root->val==val)
            return root;
        else if(root->val<val)
            return searchBST(root->right,val);
        else
            return searchBST(root->left,val);
    }
};
//非递归方式
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) 
    {
        if(root==NULL) return NULL;
        TreeNode* temp=root;
        while(temp!=NULL)
        {
            if(temp->val==val) return temp;
            else if(temp->val<val) temp=temp->right;
            else temp=temp->left;
        }
        return NULL;
    }
};

701. 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 保证原始二叉搜索树中不存在新值。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。

例如, 
给定二叉搜索树:

        4
       / \
      2   7
     / \
    1   3
和 插入的值: 5
你可以返回这个二叉搜索树:

         4
       /   \
      2     7
     / \   /
    1   3 5

分析：二叉搜索树具有良好的顺序。二叉搜索树的巨大优势就是：在平均情况下，能够在 $O(logN)$ 的时间内完成搜索和插入元素。

因此等价于找到要插入的值对应的位置即可，将插入的节点作为叶子节点的子节点插入。首先建立相应的结点，然后搜索，找到正确的位置然后插入。

• 若 val > node.val，插入到右子树。
• 若 val < node.val，插入到左子树。

//递归写法：
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) 
    {
          TreeNode* new_node=new TreeNode(val);
          if(root==NULL) return new_node;
          else if(root->val<val) root->right=insertIntoBST(root->right,val);
          else root->left=insertIntoBST(root->left,val);
          return root;
    }
};
//非递归写法：
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) 
    {
          TreeNode* new_node=new TreeNode(val);
          if(root==NULL) return new_node;
          TreeNode* pre=NULL,*temp=root; //找到插入位置，然后连接起来
          while(temp!=NULL)
          {
              pre=temp;
              if(temp->val>val) temp=temp->left;
              else temp=temp->right;
          }
          //则temp位置就是要插入的位置，pre为其父结点
          if(pre->val<val)
            pre->right=new_node;
          else
            pre->left=new_node;
        return root;

    }
};

450. 删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；如果找到了，删除它。
说明： 要求算法时间复杂度为 O(h)，h 为树的高度。

示例:
root = [5,3,6,2,4,null,7]
key = 3

    5
   / \
  3   6
 / \   \
2   4   7
给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
    5
   / \
  4   6
 /     \
2       7

另一个正确答案是 [5,2,6,null,4,null,7]。
    5
   / \
  2   6
   \   \
    4   7

分析：二叉搜索树的删除操作较为复杂，主要步骤为：找到要删除的节点，删除该节点(保持二叉树的特性)

一种可行的删除操作为：

• 如果删除的要删除的节点是叶节点，则将其删去即可

• 需要删除的节点没有左儿子，则将右儿子提上去即可

• 需要删除的节点的左儿子没有右儿子，则将左儿子提上去即可

• 以上情况均不满足，则将左儿子的子孙中最大的节点提到删除的节点处

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root==NULL) return root;
        //--------------找到要删除的节点----------
        if (root->val < key)  
        {
            root->right = deleteNode(root->right, key);     
            return root;
        }
        if (root->val > key) 
        {
            root->left = deleteNode(root->left, key);    
            return root;
        }
        // 此时的root就是要删除的节点
        if (root->left==NULL) //root的left为空，则将右子树替代root
        {
            TreeNode* tmp = root->right;   
            delete root;
            return tmp;
        }
        if (root->right==NULL)  //root的right为空，则将左子树替代root
        {
            TreeNode* tmp = root->left;  
            delete root;
            return tmp;
        }
        //都不是空的话，找到左子树中的最大值放入
        TreeNode* tmp = root->left;
        if(tmp->right==NULL)  //如果左子树没有右节点，将左子树放入即可
        {
            tmp->right=root->right;
            delete root;
            return tmp;
        }
        //否则找到左子树中最大的节点
        TreeNode* pre=root;
        while (tmp->right!=NULL) 
        {
            pre=tmp;
            tmp = tmp->right; //找到左子树的最大值
        }
        //将最大节点的值传入root，将pre->right指向tmp的left即可
        root->val=tmp->val;
        pre->right=tmp->left;
        return root;
    }
};

面试题54. 二叉搜索树的第k大节点

给定一棵二叉搜索树，请找出其中第k大的节点。

示例 1:
输入: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
输出: 4
    
示例 2:
输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 4

分析：二叉搜索树的中序遍历是递增数列，因此，中序遍历的逆数列是一个递减数列。可以用一个值记录已经遍历多少个节点，则遍历到第k个时即为所求。

如何获取中序遍历倒序数列？改变遍历顺序即可

• 先以该方式遍历右子树
• 再遍历根节点
• 再以该方式遍历左子树

class Solution 
{    private:
    	int n = 0;  //记录次数
   		int res = 0; //记录结果
    public:
    int kthLargest(TreeNode *root, int k) 
    {
        n = k;
        helper(root);
        return res;
    }
    void helper(TreeNode *root){
        if(root->right != NULL && n>0 )  
            helper(root->right);
        n--;
        if(n==0)
        {
            res = root->val;
            return;
        }
        if(root->left != NULL && n>0 )  helper(root->left);
    }
};

938. 二叉搜索树的范围和

给定二叉搜索树的根结点 root，返回 L 和 R（含）之间的所有结点的值的和。

二叉搜索树保证具有唯一的值。

示例 1：
输入：root = [10,5,15,3,7,null,18], L = 7, R = 15
输出：32
    
示例 2：
输入：root = [10,5,15,3,7,13,18,1,null,6], L = 6, R = 10
输出：23

分析:找到 L R 范围内的节点之和，因此可采用递归的方式

• 如果当前节点是NULL，返回0即可

• 如果当前节点的值小于L，说明 L-R范围内的树都在右子树，返回 右子树在该范围的和即可

• 如果当前节点的值大于R，说明 L-R范围内的树都在左子树，返回 左子树在该范围的和即可

• 否则，说明当前节点的值在 L和R之间，返回当前节点的值加上左子树、右子树在该范围的和即可

  (因为二叉搜索树的排序性，因此不需要更新L,R)

class Solution {
public:
    int rangeSumBST(TreeNode* root, int L, int R) 
    {
        if(root==NULL) return 0;
        if(root->val<L) return rangeSumBST(root->right,L,R);
        else if(root->val>R) return rangeSumBST(root->left,L,R);
        else return root->val+rangeSumBST(root->right,L,R)+rangeSumBST(root->left,L,R);
    }
};