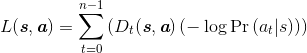深度强化学习方法——策略梯度法

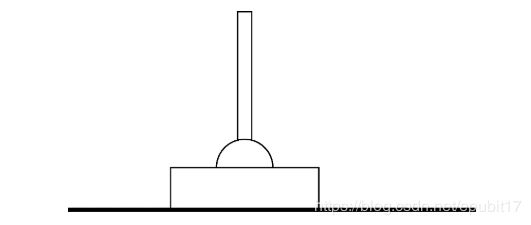
现在我们来看Open AI Gym中无法用标准列表法解决的车杆问题（cart pole）和新的深度强化学习方法——策略梯度（policy gradients）。“车杆”游戏如图6.8所示，在一维轨道上有一辆推车，一根杆子通过一个粘着的接头连接在推车上，当车被推向某个方向时，杆子的顶部会根据牛顿定律向左或向右移动。一个状态由四个值组成——前一次移动后的推车位置、当前移动后的推车位置、前一次移动后的车杆角度和当前移动后车杆角度。我们给出连续时间上的数值，使程序能够计算出运动的方向。玩家可以采取两种行动：向右或向左推动推车。推力大小总是相同。如果推车向右或向左移动太远，或者车杆顶部偏离垂直方向太远，会出现step信号表示当前游戏结束，而后需要reset以开始新游戏。我们在失败前的每一步都会得到一个单位的奖励，当然，我们的目标是尽可能长时间地将推车和车杆保持在合适位置上。由于状态对应于四元实数组，所以可能的状态数量是无限的，这使得列表法无法使用。

 

图6.8　车杆游戏

到目前为止，我们已经使用了神经网络模型来逼近MDP的Q函数。在这一节中，我们将会展示神经网络直接对策略函数进行建模的方法。我们再次讨论无模型学习，并且再次采用在游戏环境中漫游的模式，最初主要通过随机方式选择动作，后续转而使用神经网络推荐。正如本章中其他部分一样，当务之急是找到合适的损失函数，因为我们不知道采取何种行动才是正确的。

在深度Q学习中，我们一次只移动一步，并且依赖于这样一个事实：在移动之后，我们得到了奖励，并最终进入了一个新的状态，由此我们积累了更多的当前本地环境知识。我们的损失是基于旧知识的预测（如Q函数）和实际发生的情况之间的差异。

在这里，我们尝试一些不同的东西。假设我们在一次游戏的整个迭代过程中，没有对网络做任何修改——例如，在车杆顶点翻转之前，我们移动了20步（推车）。这一次，我们根据Q函数得到的概率分布来选择行动，从而进行探索/利用，而不是取Q函数最大值。

在这种情况下，我们可以计算第一个状态的折扣奖励（D0(s,a)），这个状态之后是我们刚刚尝试的所有状态和行动。

（6.9）

如果采取了n步行动，可以根据以下递归关系计算任何“状态-行动”组合（si,ai）的未来折扣奖励。

（6.10）

（6.11）

例如，我们经过的一系列状态中（当采取行动a时）的第四个状态的折扣未来奖励是D4。请再次注意，我们在这里获得了信息。例如，在我们尝试第一个随机移动序列之前，我们不知道可能的奖励是什么。在这之后我们知道，比如说，10是可能的奖励（对于一个随机的移动序列来说10确实是合理的）。又或者，我们现在知道如果在第10步翻倒，那么Q(s9, a9) = 0。

一个能够捕捉这些事实的好的损失函数是

（6.12）

要理解这个函数，首先要注意最右边的项是交叉熵损失，它本身就能鼓励网络对状态st做出响应、输出行动at。当然，这本身是非常无用的，特别是在学习开始阶段，我们是随机采取行动的。

接下来考虑Dt值如何影响损失，特别是a0对s0是错误的行动时。例如，假设开始时推车位于中间，并且车杆倾向于右边，我们选择向左移动推车，使车杆进一步向右倾斜。读者应该看到，在其他条件相同的情况下，此时D0的值比向右移动得到的值要小——原因是（其他条件相同），如果第一次移动是“好的”，杆和车保持在界限内的时间更长（n更大），D值也更大。因此，式（6.12）代入坏a0后得到的损失更大，这样就可以训练神经网络更喜欢好的a0。

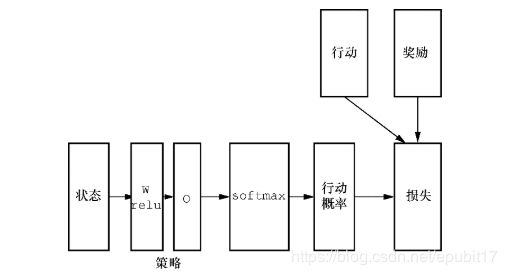
这种架构/损失函数组合被称为REINFORCE。图6.9显示了基本架构，需要注意的重点是，这里的神经网络有两种不同的使用模式。首先，从左边看，我们给神经网络输入一个单一状态，如前所述，它是一个四元实数组，表示推车和杆头的位置和速度。在这种模式下，我们得出采取两种可能行动的概率，如图6.9中间靠右部分所示。在这种模式下，我们不为奖励或行动的placeholder提供值，因为（a）我们不知道它们，（b）我们不需要它们，因为此时我们不计算损失。在我们完成整个游戏的所有动作后，我们在另一种模式下使用神经网络，这次我们给它一系列的行动和奖励，并要求它计算损失并执行反向传播。训练时，我们在某种意义上使用两种不同的方式计算行动。首先，我们向神经网络馈入所经历的状态，由策略计算层计算每个状态的行动概率。其次，我们将行动作为placeholder直接输入。这是因为在游戏模式中决定行动时，我们不一定选择概率最高的行动，而是根据行动概率随机选择。为了根据式（6.12）计算损失，我们两种模式都需要。

 

图6.9　REINFORCE的深度学习架构，其中W和O为线性单元

图6.10是使用式（6.12）的损失函数创建策略梯度神经网络的TF代码，图6.11是使用神经网络在游戏环境中学习策略并行动的伪代码。首先观察伪代码，请注意，最外面的循环（第2行）指明我们玩3,001次游戏。内循环（2(b)行）表明一直玩游戏直到step告诉我们已经完成游戏（E行）或者移动了999次后结束。我们根据神经网络（第i、ii行）得出的概率随机选择一个行动，然后在游戏中执行该行动。我们在列表hist中保存结果，以便记录所发生的事情。如果行动导致达到了最终状态，那么我们更新模型参数。

state= tf.placeholder(shape=[None,4],dtype=tf.float32)
W =tf.Variable(tf.random_uniform([4,8],dtype=tf.float32))
hidden= tf.nn.relu(tf.matmul(state,W))
O= tf.Variable(tf.random_uniform([8,2],dtype=tf.float32))
output= tf.nn.softmax(tf.matmul(hidden,O))

rewards = tf.placeholder(shape=[None],dtype=tf.float32)
actions = tf.placeholder(shape=[None],dtype=tf.int32)
indices = tf.range(0, tf.shape(output)[0]) * 2 + actions
actProbs = tf.gather(tf.reshape(output, [-1]), indices)
aloss = -tf.reduce_mean(tf.log(actProbs)*rewards)
trainOp= tf.train.AdamOptimizer(.01).minimize(aloss)

图6.10　车杆问题中，策略梯度神经网络的TF图指令

如图6.10所示，我们通过如下过程计算output：获取当前状态值state并使其通过两层神经网络，其中神经网络的两层线性单元为W和O（由tf.relu分开），然后输入softmax，将logit转换为概率。正如以前所使用的多层神经网络，其第一层的维度为[输入尺寸，隐藏层尺寸]，第二层维度为[隐藏层尺寸，输出尺寸]，其中隐藏层尺寸（hidden-size）是超参数（我们选择了8）。

因为在这里我们设计了一个新的损失函数，而没有使用TF库中的标准函数，所以损失计算必须基于更基本的TF函数建立（图6.10的后半部分）。例如，我们以前使用的所有神经网络中，前向传递和后向传递是密不可分的，因为不涉及TF之外的计算。这里我们从外部获得rewards的值——rewards是一个placeholder，根据图6.11中的行A、B和C输入。同样，actions也是一个placeholder。

 

图6.11　车杆问题中，策略梯度训练神经网络的伪代码

图6.10的最后三行看起来更加熟悉。aloss计算式（6.12）中的量。我们使用了Adam优化器。我们可以使用熟悉的梯度下降优化器，只需将它代入，再将学习率提高一倍，就可以获得还不错的性能，但没有那么好。Adam优化器是公认的高级优化器，它比梯度下降优化器稍微复杂一点。这两个优化器有几个方面不同，最根本的不同是动量（momentum）的使用。顾名思义，如果一个使用动量的优化器从最近开始一直在向上或向下移动一个参数值，那么它往往会持续地向上或向下移动一个参数值——比梯度下降移动得更多。

接下来讨论图6.10的另外两行代码，它们分别设置indices和actProbs。首先，忽略它们的工作方式，专注于它们需要做的事情，即图6.12所示的转换。左边是一个前向传递的输出，可以计算可能的行动（r和l）各自是最优行动的概率。如果是第1章，并且我们使用全监督，我们会将它乘以一个批大小的独热向量的张量，根据全监督得到我们应该采取的行动的概率。事实上，这正是图6.12右边显示的。

 

图6.12　从所有概率的张量中提取行动概率

我们依赖于gather操作实现这个转换，而gather接收两个参数，取出由数字索引指定的张量元素，并将它们放在一个新的张量中。

tf.gather(tensor, indices)

例如，如果tensor是((1,3),(4,6),(2,1),(3,3))，indices是(3,1,3)，那么输出是((3,3),(4,6),(3,3))。在本例中，我们将图6.12中左边的行动概率矩阵转换成一个概率向量，并根据前一行代码将indices设置为正确列表，因此tf.gather只收集actions向量指定的行动的概率。证明indices设置正确是留给读者的练习（练习6.5）。

可以回顾前文，更仔细地查看Q学习和REINFORCE是如何联系在一起的。首先，它们收集环境信息以通知神经网络的方式不同。一方面，Q学习移动一步，然后观察神经网络对结果的预测是否接近实际发生的情况。回顾式（6.8），即Q学习损失函数，可以发现如果预测和实际结果相同，那么就没有什么可更新的了。另一方面，使用REINFORCE时，我们在改变任何神经网络参数之前要完成一回合游戏，其中回合是指游戏从初始状态直到游戏发出结束的信号完整运行一次。请注意，我们做的和Q学习类似，但是使用REINFORCE的参数更新策略。这减慢了学习速度，因为我们更新参数的次数要少得多，但是作为补偿，我们会做出更好的改变，因为我们计算了实际的折扣奖励。

本文摘自《深度学习导论》

本书讲述了前馈神经网络、Tensorflow、卷积神经网络、词嵌入与循环神经网络、序列到序列学习、深度强化学习、无监督神经网络模型等深度学习领域的基本概念和技术，通过一系列的编程任务，向读者介绍了热门的人工智能应用，包括计算机视觉和自然语言处理等。

本书要求读者熟悉线性代数、多元微积分、概率论与数理统计知识，另外需要读者了解Python编程。

本书编写简明扼要，理论联系实践，每一章都包含习题以及补充阅读的参考文献。本书既可作为高校人工智能课程的教学用书，也可供从业者入门参考。