布隆过滤器Bloom filter基本原理
最近有碰到布隆过滤器,发现redis本身没有实现它。如果使用需要再安装这个模。
有兴趣的可以自己学习下
先看下介绍
The RedisBloom module provides four data structures: a scalable Bloom filter, a cuckoo filter, a count-min sketch, and a top-k. These data structures trade perfect accuracy for extreme memory efficiency, so they're especially useful for big data and streaming applications.
Bloom and cuckoo filters are used to determine, with a high degree of certainty, whether an element is a member of a set.
A count-min sketch is generally used to determine the frequency of events in a stream. You can query the count-min sketch get an estimate of the frequency of any given event.
A top-k maintains a list of k most frequently seen items.
简单意思就是:
RedisBloom模块提供了四种数据结构:可伸缩的Bloom filter、cuckoo filter、count-min sketch和top-k。这些数据结构以完美的准确性换取了极高的内存效率,因此它们对于大数据和流媒体应用程序特别有用。
Bloom和cuckoo过滤器用于高度精确地确定一个元素是否属于一个集合的成员。
count-min sketch 通常用于确定流中事件的频率。您可以查询count-min sketch,以获得对任何给定事件的频率的估计。
top-k维护一个包含k个最常见项的列表。
简单来说就是,利用少量内存完成大量数据处理。
下面逐个了解下
Bloom filter
使用场景
判断一个元素在不在一个集合中,我们可以用hashset,复杂度O(1)即可判断。
但是当数据量很大时,需要的存储很大。
可以考虑使用bit位来判断,但是又会有hash冲突的问题。为了降低冲突率,可以采用多个hash 来实现。
基本原理
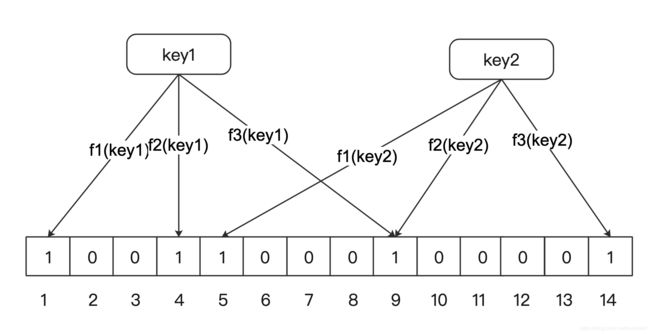
Bloom filter 本质是一个bit数组。每个元素都只占用 1 bit,每个元素只能是 0 或者 1。
对于一个key,利用 k 个hash 函数进行映射得到 n1, n2, n3。然后标记数组下标 n1, n2, n3 的位置为 1。
因为存在哈希冲突,即某个bit位已经因为其他key变成1。因此当一个key 映射的所有位置都已经是1,此时无法判断当前key是否存在。当然,如果一个key 映射的所有位置不全是1, 则说明当前key 不存在。即所谓的假正
例如,如果 "hello" 的映射为{1,4,9},此时发现这三个位置都是1,则不一定能准确判断出 "hello" 存在集合中。
公式
当hash函数个数 k = (ln2) * (m/n) 时错误率最小。
在错误率不大于e的情况下,则 m >= n*log2(1/e)*log2e
具体可以参考论文
使用方法
bf.reserve your_key 0.01 100bf.reserve 有三个参数,分别是 key, error_rate 和 initial_size 。
从上边的公式不难看出:error_rate 错误率越低,需要的空间越大。
initial_size 参数表示预计放 入的元素数量,当实际数量超出这个数值时,误判率会上升。
所以需要提前设置一个较大的数值避免超出导致误判率升高。
默认情况下 error_rate 是 0.01,默认的 initial_size 是 100。
代码实现
google的guava包中提供了BloomFilter类,直接用的是服务器内存
待续
优缺点
优点:存储数据量小,节省存储及计算空间
缺点:只能对集合添加元素,无法删除(也并非完全不能,可以使用 bloom filter 的变种 CounterBloom Filte,它将Bloom Filter每一个Bit改为一个计数器);存在误报存在的可能,即false positive rate (假正率)。
cuckoo filter
使用场景
适合大并发的读, 少量的写的应用场景。 而且空间利用率可以做到很高。cuckoo filter里不会存储原信息,但会存储指纹信息。因此,相比于Bloom filter,它既可以确保该元素存在的必然性,又可以在不违背此前提下删除任意元素,仅仅比bitmap牺牲了微量空间效率。
基本原理
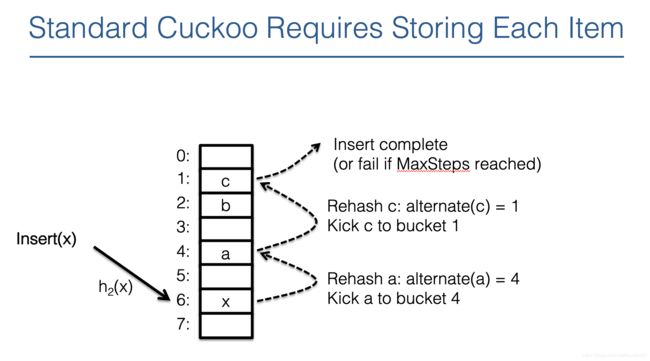
一个 key 如果哈希到某个位置,发现该位置上已经有元素 key_1 了,则把 key_1 移到 另一个位置,然后把key 放入腾出的位置上,并记录碰撞次数。如果另一个位置上还有元素,再进行移动,循环进行。
如果碰撞次数达到某个阈值则认为过滤器容量不足,需要对其进行 rehash 扩容。
这个过程类似于布谷鸟下蛋的过程,所以称其为布谷鸟过滤器。
问题:因为桶中没有存原有信息,因此计算备选桶就成了问题,解决方法如下:
即利用当前桶的位置和当前指纹的哈希值,进行异或。
参考文章和PPT
公式
在保证内存利用率高的情况下,存储n个元素,则需要 Ω(logn/b) bit位存指纹,其中 b 为桶中的槽位数
实现
这里引用论文文章里给出的代码实现
count-min sketch
使用场景
主要用于实时统计数据流中元素出现的频率,能判断某个元素出现的频率,近似值。
在数据量小的时候,可以用hashmap,但是当数据量非常大时,就需要很大的存储了,不可行。而count-min sketch只存储它们Sketch的计数,因此可行。
基本原理
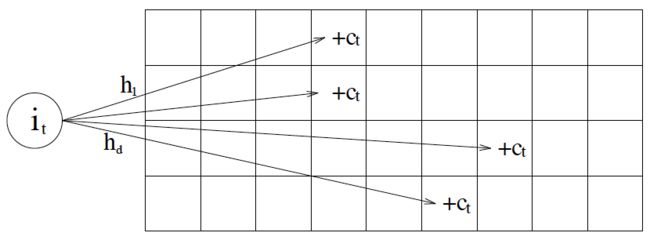
一个长度为 x 的数组,用来计数,初始每个元素的计数值为 0。当某个元素出现时,hash 到某个索引 i, 则对 x[i] 加 1 。
考虑存在哈希冲突,定义 k 个长度为 x 的数组,和 k 个哈希函数。
更新时,对 k 个哈希函数算的位置上的值加 1。 即图中行的Ct 都加 1
查询频率时,对k个哈希函数算出的位置上的值,取最小。即 min( Ct1, Ct2, ... Ctk)
公式
理论及 w 和 k 的取值,参考论文
前面提到的 redisBloom 代码里,实现如下:
CMSketch *NewCMSketch(size_t width, size_t depth) {
assert(width > 0);
assert(depth > 0);
CMSketch *cms = CMS_CALLOC(1, sizeof(CMSketch));
cms->width = width;
cms->depth = depth;
cms->counter = 0;
cms->array = CMS_CALLOC(width * depth, sizeof(uint32_t));
return cms;
}根据参数 width, depth 申请一个长度为 width * depth 的数组,来代替上边说的二维哈希结构。
插入元素时,循环 hash 函数个数,即depth 次
size_t CMS_IncrBy(CMSketch *cms, const char *item, size_t itemlen, size_t value) {
assert(cms);
assert(item);
size_t maxCount = 0;
for (size_t i = 0; i < cms->depth; ++i) {
uint32_t hash = CMS_HASH(item, itemlen, i);
cms->array[(hash % cms->width) + (i * cms->width)] += value;
maxCount = max(maxCount, cms->array[(hash % cms->width) + (i * cms->width)]);
}
cms->counter += value;
return maxCount;
}查询时,则循环 depth 次,最后取 最小值;
size_t CMS_Query(CMSketch *cms, const char *item, size_t itemlen) {
assert(cms);
assert(item);
size_t temp = 0, res = (size_t)-1;
for (size_t i = 0; i < cms->depth; ++i) {
uint32_t hash = CMS_HASH(item, itemlen, i);
temp = cms->array[(hash % cms->width) + (i * cms->width)];
if (temp < res) {
res = temp;
}
}
return res;
}
优点:只需要固定大小的内存和计算时间,和需要统计的元素多少无关;
缺点:只会估算偏大,永远不会偏小;对于低频的元素,估算值相对的错误可能会很大。
个人感觉它是 HyperLogLog 的一个补充,HyperLogLog 只能 统计去重的数据量,但是不能计算频率。
对此,文章《New estimation algorithms for streaming data: Count-min can do more》提出了 Count-Mean-Min Sketch。在查询时利用降噪来提高准确率。
具体:
插入:和Count-min Sketch一样;
查询:假设查询到 d 个hash函数在 d * w 的数组中,查到的数量分别时 Ct1,Ct2,.. Ctd,对每行,除去Ctd, 剩下的元素均匀分布,则噪音为该行剩余元素的平均值,因此Ctd 降噪后应该是 Ctd - mean(该行剩余元素)。
然后取 d 个 降噪后的中位数,即频次为 median(Ctd - mean(该行剩余元素))
当然还有其他变种的Sketch,可以参考文章
top-k
使用场景
top-k 有基本的top-k 和 top-k 频繁项之分
基本的top-k顾名思义,即海量数据取最大或最小的K个值。
可能想到的方案:
1.直接排序后取前 k 个。复杂度 O(n logn) ,当一亿条数据时,就不可行了。
2.构建 k 个元素的大顶堆(小顶堆),遍历所有元素,最后堆里的元素排序输出。O(k * logk) + O(n * logk)。如果不需要排序即O(n * logk)
3.使用快排中的partition,即BFPRT。利用随机某个元素key 对n个元素分组,大于等于 key 的集合为SL,小于 key 的为SM。若SL 大于k个元素,则在 SL中递归找,否则在 SM 中找 k - len(SL) 个元素。同过递归将问题分解。复杂度O(n)
这就是平常所说的Top-K问题
而标题的Top-K 频繁项,则是寻找数据流中出现最频繁的k个元素,即 find top k frequent items in a data stream。
方案:
1.用一个容量为k的小顶堆,维护目前最频繁的前 k 个元素,同时用一个HashMap 维护元素与出现次数的映射。
2.元素出现,则把 HashMap 的计数加 1(不存在则初始为 1)
3.同时在堆里查找该元素:a)找到则把堆里的计数加 1,并调整堆。b)找不到,则将当前元素出现次数与堆顶比较,如果比堆顶大,则替换,并调整堆。
空间复杂度:O(n)
时间复杂度:每次查找堆 O(k),调整堆 O(logk)。n个元素下来,复杂度 O(n*(k+logk))。k比较小,即 O(n)
海量数据时,就不可行了,除非利用多台机器分解。
基本原理
Top-K 则是对上边方案的改进,将 HashMap 维护计数 改成 Count-Min Sketch 维护计数。
空间复杂度:只需要一个非常小的数组,加 O(k) 的堆
时间复杂度:同上
具体理论可以参考论文《HeavyKeeper: An Accurate Algorithm for Finding Top-k Elephant Flows》
优缺点
参考:
《流数据库 概率计算概念 - PipelineDB-Probabilistic Data Structures & Algorithms》
《Probabilistic Data Structures for Web Analytics and Data Mining》
《Approximating Data with the Count-Min Data Structure》